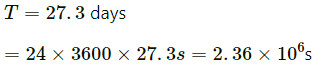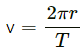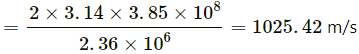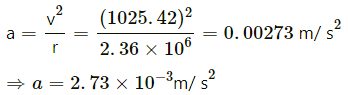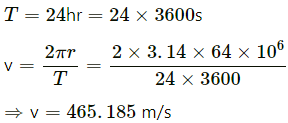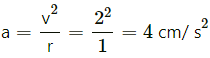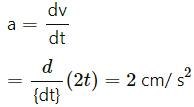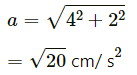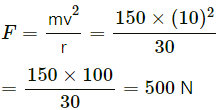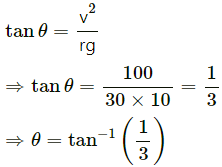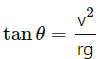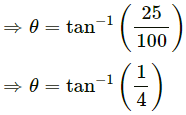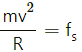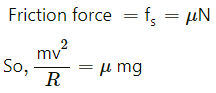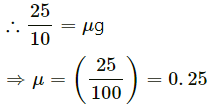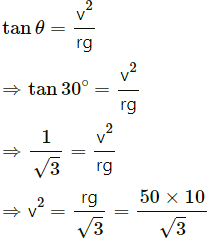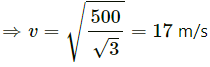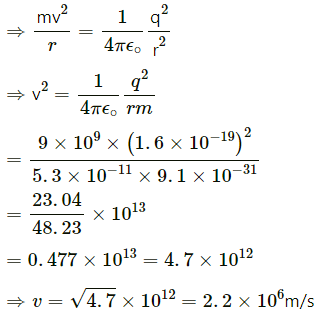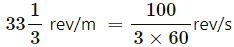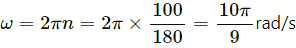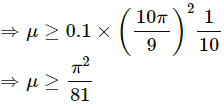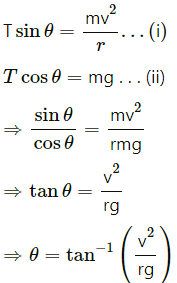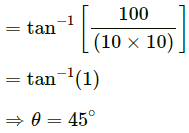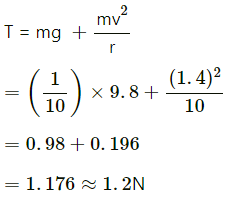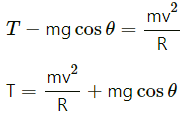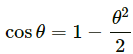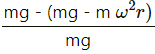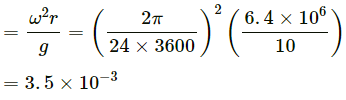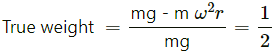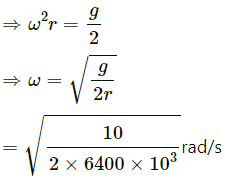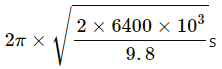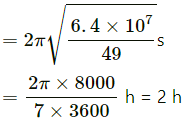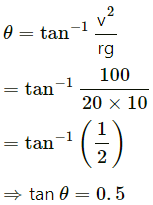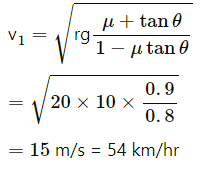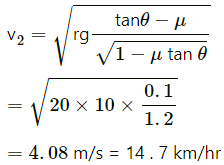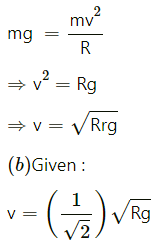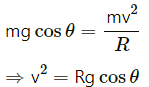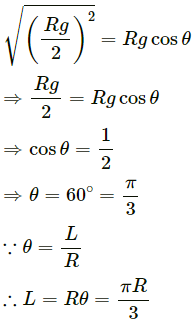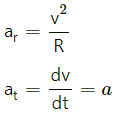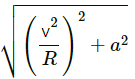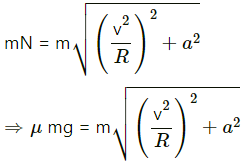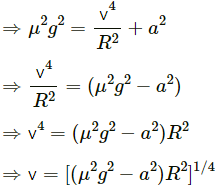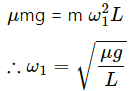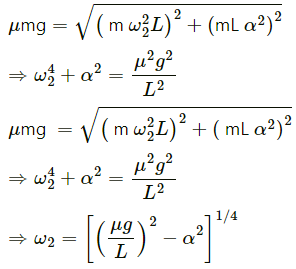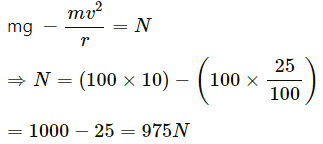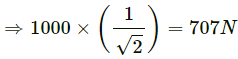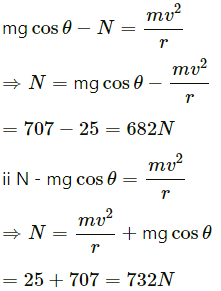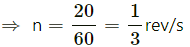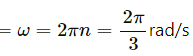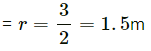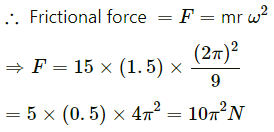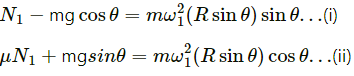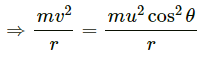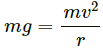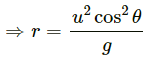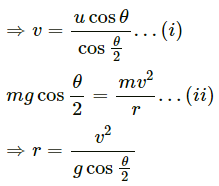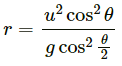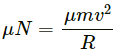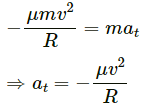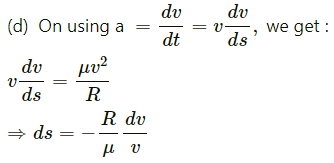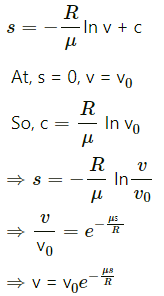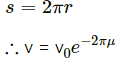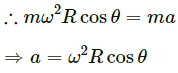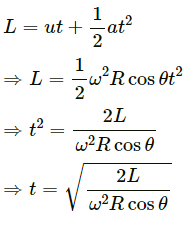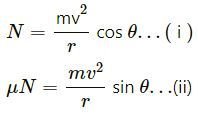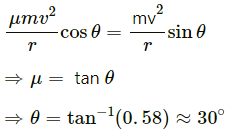HC Verma Questions and Solutions: Chapter 7- Circular Motion- 2 | HC Verma Solutions - JEE PDF Download
Exercise
Q.1. Find the acceleration of the moon with respect to the earth from the following data : Distance between the earth and the moon = 3.85 × 105 km and the time taken by the moon to complete one revolution around the earth = 27.3 days.
Distance between the Earth and the Moon :
Time taken by the Moon to revolve around the Earth :
Velocity of the Moon :
Acceleration of the Moon:
Q.2. Find the acceleration of a particle placed on the surface of the earth at the equator due to earth's rotation. The diameter of earth = 12800 km and it takes 24 hours for the earth to complete one revolution about its axis.
Diameter of the Earth = 12800 km
So, radius of the Earth, R = 6400 km = 6.4 × 106 m
Time period of revolution of the Earth about its axis :
Acceleration of the particle: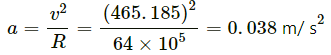
Q.3. A particle moves in a circle of radius 1.0 cm at a speed given by v = 2.0 t where v is cm/s and t in seconds.
(a) Find the radial acceleration of the particle at t = 1 s.
(b) Find the tangential acceleration at t = 1 s.
(c) Find the magnitude of the acceleration at t = 1 s.
Speed is given as a function of time. Therefore, we have:
v = 2t
Radius of the circle = r = 1 cm
At time t = 2 s, we get :
(a) Radial acceleration
(b) Tangential acceleration
(c) Magnitude of acceleration
Q.4. A scooter weighing 150 kg together with its rider moving at 36 km/hr is to take a turn of a radius 30 m. What horizontal force on the scooter is needed to make the turn possible?
Given:
Mass = m = 150 kg
Speed = v = 36 km/hr = 10 m/s
Radius of turn = r = 30 m
Let the horizontal force needed to make the turn be F. We have :
Q.5. If the horizontal force needed for the turn in the previous problem is to be supplied by the normal force by the road, what should be the proper angle of banking?
Given:
Speed of the scooter = v = 36 km/hr = 10 m/s
Radius of turn = r = 30 m
Let the angle of banking be θ
We have :
Q.6. A park has a radius of 10 m. If a vehicle goes round it at an average speed of 18 km/hr, what should be the proper angle of banking?
Given:
Speed of the vehicle = v = 18 km/h = 5 m/s
Radius of the park = r = 10 m
Let the angle of banking be θ
Thus, we have :
Q.7. If the road of the previous problem is horizontal (no banking), what should be the minimum friction coefficient so that scooter going at 18 km/hr does not skid?
If the road is horizontal (no banking),
we have :
N = mg
Here, fs is the force of friction and N is the normal reaction.
If μ is the friction coefficient, we have :
Here,
Velocity = v = 5 m/s
Radius = R = 10 m
Q.8. A circular road of radius 50 m has the angle of banking equal to 30°. At what speed should a vehicle go on this road so that the friction is not used?
Given:
Angle of banking = θ = 30°
Radius = r = 50 m
Assume that the vehicle travels on this road at speed v so that the friction is not used.
We get :
Q.9. In the Bohr model of hydrogen atom, the electron is treated as a particle going in a circle with the centre at the proton. The proton itself is assumed to be fixed in an inertial frame. The centripetal force is provided by the Coulomb attraction. In the ground state, the electron goes round the proton in a circle of radius 5.3 × 10−11 m. Find the speed of the electron in the ground state. Mass of the electron = 9.1 × 10−31 kg and charge of the electron = 1.6 × 10−19 C.
Given:
Radius of the orbit of the ground state = r = 5.3 x 10-11 m
Mass of the electron = m = 9.1 x 10-31 kg
Charge of electron = q = 1.6 x 10-19c
We know:
Centripetal force = Coulomb attraction
Therefore, we have :
Q.10. A stone is fastened to one end of a string and is whirled in a vertical circle of radius R. Find the minimum speed the stone can have at the highest point of the circle.
Let m be the mass of the stone.
Let v be the velocity of the stone at the highest point.
R is the radius of the circle.
Thus, in a vertical circle and at the highest point,
we have :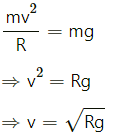
Q.11. A ceiling fan has a diameter (of the circle through the outer edges of the three blades) of 120 cm and rpm 1500 at full speed. Consider a particle of mass 1 g sticking at the outer end of a blade. How much force does it experience when the fan runs at full speed? Who exerts this force on the particle? How much force does the particle exert on the blade along its surface?
Diameter of the fan = 120 cm
∴ Radius of the fan = r = 60 cm = 0.6 m
Mass of the particle = M = 1 g = 0.001 kg
Frequency of revolutions = n = 1500 rev/min = 25 rev/s
Angular velocity = ω = 2πn = 2π x 25 = 57.14 rev/s
Force of the blade on the particle:
F = Mrw2
= (0.001) × 0.6 × (157.14)2
= 14.8 N
The moving fan exerts this force on the particle.
The particle also exerts a force of 14.8 N on the blade along its surface.
Q.12. A mosquito is sitting on an L.P. record disc rotating on a turn table at 33(1/3) revolutions per minute. The distance of the mosquito from the centre of the turn table is 10 cm. Show that the friction coefficient between the record and the mosquito is greater than π2/81. Take g =10 m/s2.
Frequency of disc = n =
Angular velocity =
r = 10 cm = 0 . 1 m
g = 10 m/s2
It is given that the mosquito is sitting on the L.P. record disc. Therefore, we have : Friction force ≥ Centrifugal force on the mosquito
⇒ μmg ≥ mrω2
⇒ μ ≥ rω2/g
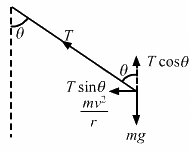
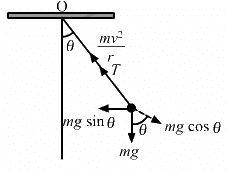
Q.13. A simple pendulum is suspended from the ceiling of a car taking a turn of radius 10 m at a speed of 36 km/h. Find the angle made by he string of the pendulum with the vertical if this angle does not change during the turn. Take g = 10 m/s2.
Speed of the car = v = 36 km/hr = 10 m/s
Acceleration due to gravity = g = 10 m/s2
Let T be the tension in the string when the pendulum makes an angle θ with the vertical.
From the figure, we get :
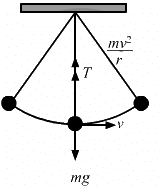
Q.14. The bob of a simple pendulum of length 1 m has mass 100 g and a speed of 1.4 m/s at the lowest point in its path. Find the tension in the string at this instant.
Given:
Mass of the bob = m = 100 gm = 0.1 kg
Length of the string = r = 1 m
Speed of bob at the lowest point in its path = 1.4 m/s
Let T be the tension in the string.
From the free body diagram,
we get :
Q.15. Suppose the bob of the previous problem has a speed of 1.4 m/s when the string makes an angle of 0.20 radian with the vertical. Find the tension at this instant. You can use cos θ ≈ 1 − θ2/2 and SINθ ≈ θ for small θ.
Given:
Mass of the bob = m = 0.1 kg
Length of the circle = R = 1 m
Velocity of the bob = v = 1.4 m/s
Let T be the tension in the string when it makes an angle of 0.20 radian with the vertical.
From the free body diagram, we get :
For small θ, it is given that :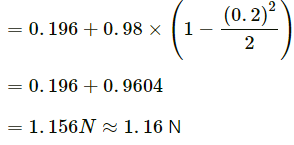
Q.16. Suppose the amplitude of a simple pendulum having a bob of mass m is θ0. Find the tension in the string when the bob is at its extreme position.
Let T be the tension in the string at the extreme position.
Velocity of the pendulum is zero at the extreme position.
So, there is no centripetal force on the bob.
∴ T = mgcosθ0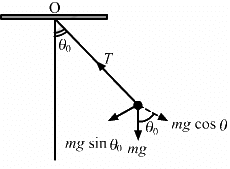
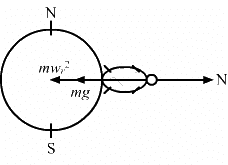
Q.17.1. A person stands on a spring balance at the equator. By what fraction is the balance reading less than his true weight?
Balance reading = Normal force on the balance by the Earth.
At equator, the normal force (N) on the spring balance :
N = mg − mω2r
True weight = mg
Therefore, we have :
Fraction less than the true weight =
Q.17.2. A person stands on a spring balance at the equator. If the speed of earth's rotation is increased by such an amount that the balance reading is half the true weight, what will be the length of the day in this case?
When the balance reading is half, we have :
∴ Duration of the day =
Q.18. A turn of radius 20 m is banked for the vehicles going at a speed of 36 km/h. If the coefficient of static friction between the road and the tyre is 0.4, what are the possible speeds of a vehicle so that it neither slips down nor skids up?
Given:
Speed of vehicles = v = 36 km/hr = 10 m/s
Radius = r = 20 m
Coefficient of static friction = μ = 0.4
Let the road be banked with an angle θ
We have :
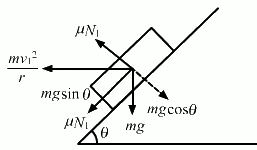
When the car travels at the maximum speed, it slips upward and μN1 acts downward.
Therefore we have :
On solving the above equations, we get :
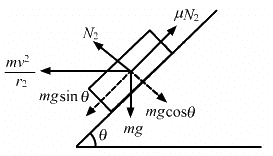
Similarly, for the other case, it can be proved that :
Thus, the possible speeds are between 14.7 km/hr and 54 km/hr so that the car neither slips down nor skids up.
Q.19. A motorcycle has to move with a constant speed on an over bridge which is in the form of a circular arc of radius R and has a total length L. Suppose the motorcycle starts from the highest point.(a) What can its maximum velocity be for which the contact with the road is not broken at the highest point? (b) If the motorcycle goes at speed 1/√2 times the maximum found in part (a), where will it lose the contact with the road? (c) What maximum uniform speed can it maintain on the bridge if it does not lose contact anywhere on the bridge?
R = Radius of the bridge
L = Total length of the over bridge
(a) At the highest point:
Let m be the mass of the motorcycle and v be the required velocity.
Suppose it loses contact at B.
At point B, we get :
Putting the value of v we get :
So, it will lose contact at a distancefrom the highest point.
(c) Let the uniform speed on the bridge be v. The chances of losing contact is maximum at the end bridge. We have :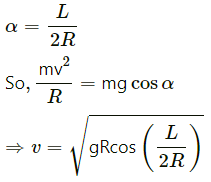
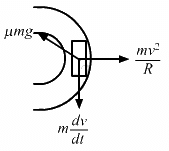
Q.20. A car goes on a horizontal circular road of radius R, the speed increasing at a constant rate dv/dt = a. The friction coefficient between the road and the tyre is μ. Find the speed at which the car will skid.
Let v be the speed of the car.
Since the motion is non-uniform, the acceleration has both radial (ar) and tangential (at) components.
Resultant magnitude =
From free body diagram, we have :
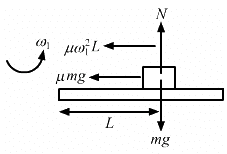
Q.21. A block of mass m is kept on a horizontal ruler. The friction coefficient between the ruler and the block is μ. The ruler is fixed at one end and the block is at a distance L from the fixed end. The ruler is rotated about the fixed end in the horizontal plane through the fixed end. (a) What can the maximum angular speed be for which the block does not slip? (b) If the angular speed of the ruler is uniformly increased from zero at an angular acceleration α, at what angular speed will the block slip?
(a) Given:
Mass of the block = m
Friction coefficient between the ruler and the block = μ
Let the maximum angular speed be ω1 for which the block does not slip
Now, for the uniform circular motion in the horizontal plane, we have :
(b) Let the block slip at an angular speed ω2.
For the uniformly accelerated circular motion, we have :
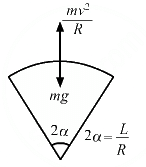
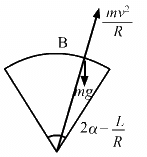
Q.22. A track consists of two circular parts ABC and CDE of equal radius 100 m and joined smoothly as shown in figure. Each part subtends a right angle at its centre. A cycle weighing 100 kg together with the rider travels at a constant speed of 18 km/h on the track. (a) Find the normal contact force by the road on the cycle when it is at B and at D. (b) Find the force of friction exerted by the track on the tyres when the cycle is at B, C and. (c) Find the normal force between the road and the cycle just before and just after the cycle crosses C. (d) What should be the minimum friction coefficient between the road and the tyre, which will ensure that the cyclist can move with constant speed? Take g = 10 m/s2.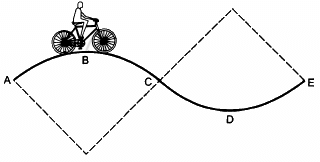
Given:
Radius of the curves = r = 100 m
Mass of the cycle = m = 100 kg
Velocity = v = 18 km/hr = 5 m/s
(a) At B, we have :
At D, we have :
(b) At B and D, we have:
Tendency of the cycle to slide is zero.
So, at B and D, frictional force is zero.
At C, we have :
mgsinθ = f
(c) i Before C,
(d) To find the minimum coefficient of friction, we have to consider a point where N is minimum or a point just before c .
Therefore, we have :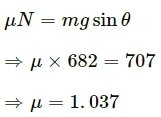
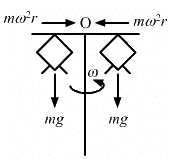
Q.23. In a children's park a heavy rod is pivoted at the centre and is made to rotate about the pivot so that the rod always remains horizontal. Two kids hold the rod near the ends and thus rotate with the rod (In the following figure). Let the mass of each kid be 15 kg, the distance between the points of the rod where the two kids hold it be 3.0 m and suppose that the rod rotates at the rate of 20 revolutions per minute. Find the force of friction exerted by the rod on one of the kids.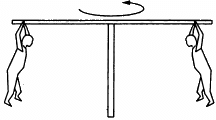
Given :
Frequency of rod = n = 20 rev per min
Therefore, we have :
angular velocity of rod ,
Angular velocity of rod
Mass of each kid = m = 15 kg
Radius
Thus, the force of frictional on one of the kids is 10π.
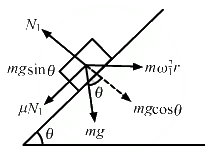
Q.24. A hemispherical bowl of radius R is rotated about its axis of symmetry which is kept vertical. A small block is kept in the bowl at a position where the radius makes an angle θ with the vertical. The block rotates with the bowl without any slipping. The friction coefficient between the block and the bowl surface is μ. Find the range of the angular speed for which the block will not slip.
When the bowl rotates at maximum angular speed, the block tends to slip upwards.
Also, the frictional force acts downward.
Here, we have:
Radius of the path that the block follow = r = Rsinθ
Let N1 be the normal reaction on the block and ω1 be the angular velocity after which the block will slip.
From the free body diagram-1, we get :
On solving the two equation, we get :
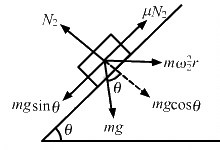
Let us now find the minimum speed (ω2) on altering the direction of μ (as shown in figure):
Hence, the range of speed is between ω2 and ω1.
Q.25. A particle is projected with a speed u at an angle θ with the horizontal. Consider a small part of its path near the highest position and take it approximately to be a circular arc. What is the radius of this circular circle? This radius is called the radius of curvature of the curve at the point.
At the highest point, the vertical component of velocity is zero.
So, at the highest point, we have:
velocity = v = ucosθ
Centripetal force on the particle = mv2/r
At the highest point, we have :
Here, r is the radius of curvature of the curve at the point.
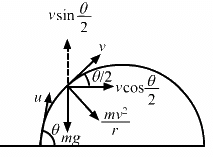
Q.26. What is the radius of curvature of the parabola traced out by the projectile in the previous problem at a point where the particle velocity makes an angle θ/2 with the horizontal?
Let u be the initial velocity and v be the velocity at the point where it makes an angle θ/2 with the horizontal component.
It is given that the horizontal component remains unchanged.
Therefore, we get :
On substituting the value of v from equation (i), we get :
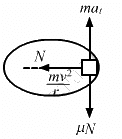
Q.27. A block of mass m moves on a horizontal circle against the wall of a cylindrical room of radius R. The floor of the room on which the block moves is smooth but the friction coefficient between the wall and the block is μ. The block is given an initial speed v0. As a function of the speed v writes
(a) the normal force by the wall on the block,
(b) the frictional force by a wall, and
(c) the tangential acceleration of the block.
(d) Integrate the tangential acceleration 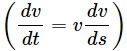 to obtain the speed of the block after one revolution.
to obtain the speed of the block after one revolution.
Given:
Radius of the room = R
Mass of the block = m
(a) Normal reaction by the wall on the block = N = mv2/R
(b) Force of frictional by the wall =
(c) Let at be the tangential acceleration of the block.
From figure, we get :
Integrating both side, we get :
For one rotation, we have :
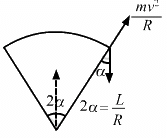
Q.28. A table with smooth horizontal surface is fixed in a cabin that rotates with a uniform angular velocity ω in a circular path of radius R (In the following figure). A smooth groove AB of length L(<<R) is made the surface of the table. The groove makes an angle θ with the radius OA of the circle in which the cabin rotates. A small particle is kept at the point A in the groove and is released to move at the point A in the groove and is released to move along AB. Find the time taken by the particle to reach the point B.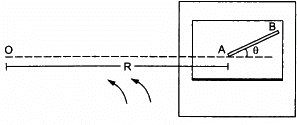
Let the mass of the particle be m.
Radius of the path = R
Angular velocity = ω
Force experienced by the particle = mω2R
The component of force mRω2 along the line AB (making an angle with the radius) provides the necessary force to the particle to move along AB.
Let the time taken by the particle to reach the point B be t.
On using equation of motion, we get :
Q.29. A car moving at a speed of 36 km/hr is taking a turn on a circular road of radius 50 m. A small wooden plate is kept on the seat with its plane perpendicular to the radius of the circular road (In the following figure). A small block of mass 100 g is kept on the seat which rests against the plate. the friction coefficient between the block and the plate is. (a) Find the normal contact force exerted by the plate on the block. (b) The plate is slowly turned so that the angle between the normal to the plate and the radius of the road slowly increases. Find the angle at which the block will just start sliding on the plate.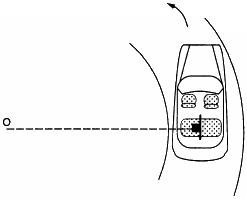
Given :
Speed of the car = v = 36 km/h = 10 m/s
Radius of the road = r = 50 m
Friction coefficient between the block and the plate = μ = 0.58
Mass of the small body = m = 100 g = 0.1 kg
(a) Let us find the normal contact force (N) exerted by the plant of the block.
(b) The plate is turned; so, the angle between the normal to the plate and the radius of the rod slowly increases.
Therefore, we have :
On using i and ii , we get :
Q.30. A table with smooth horizontal surface is placed in a circle of a large radius R (In the following figure). A smooth pulley of small radius is fastened to the table. Two masses m and 2m placed on the table are connected through a string going over the pulley. Initially the masses are held by a person with the string along the outward radius and then the system is released from rest (with respect to the cabin). Find the magnitude of the initial acceleration of the masses as seen from the cabin and the tension in the string.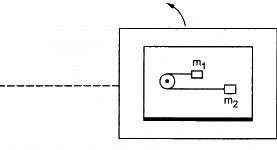
Let the bigger mass accelerates towards left with acceleration a.
Let T be the tension in the string and ω be the angular velocity of the table.
From the free body diagram, we have :
On subtracting eq. (i) by eq. (ii), we get:
Substituting the value of a in eq. (i), we get :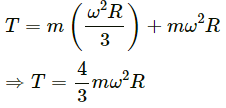
|
134 docs
|