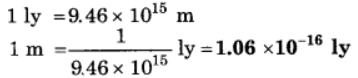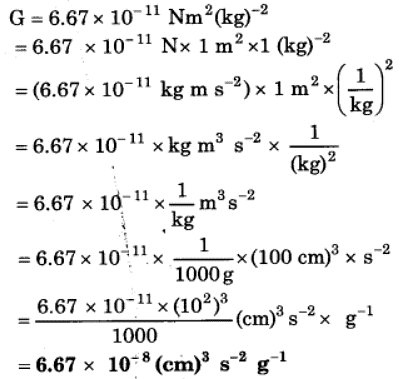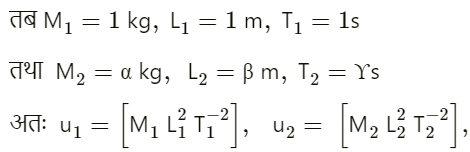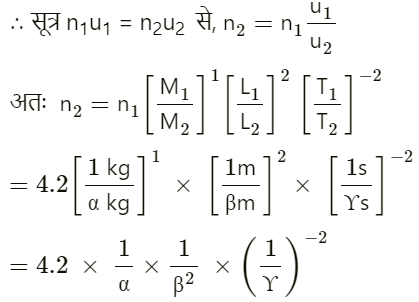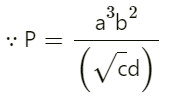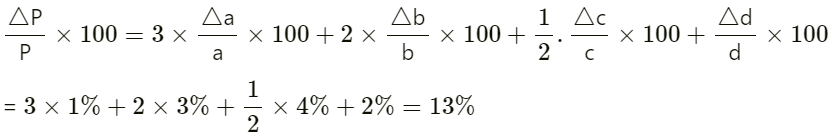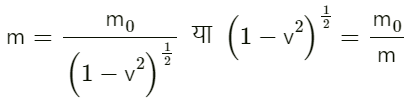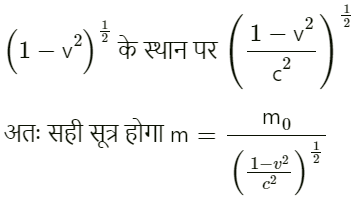मात्रक और मापन (Units & Measurement) NCERT Solutions | NCERT Textbooks in Hindi (Class 6 to Class 12) - CTET & State TET PDF Download

अभ्यास

प्रश्न.1. रिक्त स्थान भरिए
(a) किसी 1 cm भुजा वाले घन का आयतन ______ m³ के बराबर है।
(b) किसी 2 cm त्रिज्या व 10 cm ऊँचाई वाले सिलिण्डर का पृष्ठ क्षेत्रफल ______ (mm)² बराबर है।
(c) कोई गाड़ी 18 kmem/h की चाल से चल रही है तो यह 1s में ______ m चलती है।
(d) सीसे का आपेक्षिक घनत्व 11.3 है। इसका घनत्व ______ g cm^-3 या ______ kg m^-3 है।

(a) ∵ घन का आयतन = ( भुजा)³ =(1 cm)³
= (1/100 m)³ = (10^-2 m)³ [ 1cm = 1/100 = 10^-2 m)
= 10^-6 m³
(b) सिलिण्डर का पृष्ठ क्षेत्रफल = वक्र पृष्ठ का क्षेत्रफल + दोनों वृत्तीय सिरों का क्षेत्रफल 
= 2πrh + 2πr²
= 2π (h + r) = 2 x 3.14 x 2 cm (10 cm + 2 cm)
= 4 x 3 : 4 x 12cm² = 150.72 cm²
= 150.72 x (10mm)² (∵ 1 cm = 10 mm)
= 150.72 x 100(mm)² =1.5x 104 (mm)²
(c) गाड़ी की चाल = 18km/h
= 18 x 5/18 m/s = 5 m s^-1
∴ 1s में तय दूरी = चाल x समय = 5ms^-1 x 1 s = 5m
(d) सीसे का घनत्व = सीसे का आपेक्षिक-घनत्व x जल का घनत्व
= 11.3 x 1 g cm^-3 = 11.3 g cm^-3
[∵जल का घनत्व = 1 g cm^-3 या 10 kg m^-3]
या   सीसे का घनत्व = 11.3 x 10³ kg m^-3
= 1.13 x 10⁴ kg m^-3 

प्रश्न.2. रिक्त स्थानों को मात्रकों के उचित परिवर्तन द्वारा भरिए
(a) 1 kg m² s^-2 = ______ g cm² s^-2
(b) 1 m = ______ 1y
(c) 3.0 m s^-2 = ______ km h^-2
(d) G = 6.67 x 10^-11 Nm (kg)-2 = ______ (cm)³ s^-2 g^-1

(a) 1 kg = 10³ g
1 m² = 10⁴ cm²
1 kg m² s^–2 = 1 kg × 1 m² × 1 s^–2
=10³ g × 10⁴ cm² × 1 s^–2 = 10⁷ g cm² s^–2
(b)

(c)

(d)

प्रश्न.3. ऊष्मा (परागमन में ऊर्जा) का मात्रक कैलोरी है और यह लगभग 4.2 J के बराबर है, जहाँ 1 J =1 kg m² s^-2 मान लीजिए कि हम मात्रकों की कोई ऐसी प्रणाली उपयोग करते हैं जिसमें द्रव्यमान का मात्रक α kg के बराबर है, लंबाई का मात्रक β m के बराबर है, समय का मात्रक γs के बराबर है। यह प्रदर्शित कीजिए कि नए मात्रकों के पदों में कैलोरी का परिमाण 4.2 α^-1 β^-2 γ² है।  

1 कैलोरी = 4.2.J = 4.2 kg-m²S^-2
ऊर्जा का विमीय सूत्र = [ML²F^-2]
माना दी गई दो मापन पद्धतियों में द्रव्यमान, लंबाई तथा समय के मात्रक क्रमशः M₁,L₁, T₁, तथा M₂,L₂, T₂, हैं।

= 4.2 α^-1 β^-2 ϒ² 

अर्थात दूसरी पद्धति में 1 कैलोरी का मान 4.2 α^-1 β^-2 ϒ²  है।

प्रश्न.4. इस कथन की स्पष्ट व्याख्या कीजिए : तुलना के मानक का विशेष उल्लेख किए बिना “किसी विमीय राशि को ‘बड़ा या छोटा कहना अर्थहीन है।” इसे ध्यान में रखते हुए नीचे दिए गए कथनों को जहाँ कहीं भी आवश्यक हो, दूसरे शब्दों में व्यक्त कीजिए
(a) परमाणु बहुत छोटे पिण्ड होते हैं।
(b) जेट वायुयान अत्यधिक गति से चलता है।
(c) बृहस्पति का द्रव्यमान बहुत ही अधिक है।
(d) इस कमरे के अन्दर वायु में अणुओं की संख्या बहुत अधिक है।
(e) इलेक्ट्रॉन, प्रोटॉन से बहुत भारी होता है।
(f) ध्वनि की गति प्रकाश की गति से बहुत ही कम होती है।

सामान्यतया कहा जाता है कि परमाणु बहुत छोटा गोलीय पिण्ड है, परन्तु हम जानते हैं कि इलेक्ट्रॉन परमाणु से भी छोटा कण है, तब यह कहा जा सकता है कि इलेक्ट्रॉन की तुलना में परमाणु एक बड़ा पिण्ड है। इसके विपरीत क्रिकेट की गेंद की तुलना में परमाणु एक बहुत छोटा पिण्ड है। इस प्रकार हम देखते हैं कि परमाणु को किसी एक वस्तु की तुलना में बहुत छोटा कहा जा सकता है जबकि किसी अन्य वस्तु की तुलना में उसे बड़ा (UPBoardSolutions.com) कहा जा सकता है। यही बात किसी विमीय राशि के विषय में भी लागू होती है। कोई विमीय राशि, किसी दूसरी समान विमीय राशि की तुलना में बड़ी हो सकती है जबकि किसी अन्य, समान विमीय राशि से छोटी हो सकती है। अत: किसी विमीय राशि को छोटा या बंड़ा कहना तब तक अर्थहीन है जब तक कि तुलना के मानक को स्पष्ट उल्लेख ने किया गया हो।
(a) चीनी के एक दाने की तुलना में परमाणु बहुत छोटे पिण्ड होते हैं।

(b) जेट वायुयान, रेलगाड़ी की तुलना में अत्यधिक गति से चलता है।

(c) बृहस्पति का द्रव्यमान, पृथ्वी के द्रव्यमान की तुलना में बहुत ही अधिक है।

(d) इस कमरे के अन्दर वायु में अणुओं की संख्या, एक ग्राम-अणु गैस में उपस्थित अणुओं की संख्या ‘ से बहुत अधिक है। कथनों

(e) तथा

(f) को बदलने की आवश्यकता नहीं है।

प्रश्न.5. लम्बाई का कोई ऐसा नया मात्रक चुना गया है जिसके अनुसार निर्वात में प्रकाश की चाल 1 है। लम्बाई के नए मात्रक के पदों में सूर्य तथा पृथ्वी के बीच की दूरी कितनी है, प्रकाश इस दूरी को तय करने में 8 min और 20 s लगाता है।

प्रकाश की चाल = 1 मात्रक S^-1

जबकि प्रकाश द्वारा लिया गया समय है t = 8 min 20 s

= (8 x 60 + 20) s = 500s

∴ सूर्य तथा पृथ्वी के बीच की दूरी = प्रकाश की चाल x लगा समय

= 1 मात्रक s^-1 x 500 s

= 500 मात्रक

प्रश्न.6. लम्बाई मापने के लिए निम्नलिखित में से कौन-सा सबसे परिशुद्ध यन्त्र है
(a) एक वर्नियर कैलीपर्स जिसके वर्नियर पैमाने पर 20 विभाजन हैं।
(b) एक स्क्रूगेज जिसका चूड़ी अन्तराल 1 mm और वृत्तीय पैमाने पर 100 विभाजन हैं।
(c) कोई प्रकाशिक यन्त्र जो प्रकाश की तरंगदैर्घ्य की सीमा के अन्दर लम्बाई माप सकता है।

प्रश्न.7. कोई छात्र 100 आवर्धन के एक सूक्ष्मदर्शी के द्वारा देखकर मनुष्य के बाल की मोटाई मापता है। वह 20 बार प्रेक्षण करता है और उसे ज्ञात होता है कि सूक्ष्मदर्शी के दृश्य क्षेत्र में बाल की औसत मोटाई 3.5 mm है। बाल की मोटाई का अनुमान क्या है?

प्रश्न.8. निम्नलिखित के उत्तर दीजिए:
(a) आपको एक धागा और मीटर पैमाना दिया जाता है। आप धागे के व्यास का अनुमान किस प्रकार लगाएँगे?
(b) एक स्क्रूगेज का चूड़ी अन्तराल 1.0 mm है और उसके वृत्तीय पैमाने पर 200 विभाजन हैं। क्या आप यह सोचते हैं कि वृत्तीय पैमाने पर विभाजनों की संख्या स्वेच्छा से बढ़ा देने पर स्क्रूगेज की यथार्थता में वृद्धि करना संभव है?
(c) वर्नियर कैलीपर्स द्वारा पीतल की किसी पतली छड़ का माध्य व्यास मापा जाना है। केवल 5 मापनों के समुच्चय की तुलना में व्यास के 100 मापनों के समुच्चय के द्वारा अधिक विश्वसनीय अनुमान प्राप्त होने की सम्भावना क्यों है?

(a) इसके लिए हम एक बेलनाकार छड के ऊपर धागे को इस प्रकार लपेटेंगे कि धागे के फेरे एक-दूसरे से सटे रहें। धागे के फेरों द्वारा घेरी गई छड़ की लम्बाई l को मीटर पैमाने की सहायता से नाप लेंगे। अब लपेटे गए फेरों की संख्या n को गिन लिया जाएगा।

 
 

प्रश्न.9. किसी मकान का फोटोग्राफ 35 mm स्लाइड पर 1.75 cm² क्षेत्र घेरता है। स्लाइड को | किसी स्क्रीन पर प्रक्षेपित किया जाता है और स्क्रीन पर मकान का क्षेत्रफल 1.55 m² है। प्रक्षेपित्र-परदा व्यवस्था का रेखीय आवर्धन क्या है?

स्लाइड पर मकान का क्षेत्रफल = 1.75 cm²
स्क्रीन पर मकान का क्षेत्रफल = 1.55 m² = 1.55 (100 cm)
= 1.55 x 10000 cm²

 

प्रश्न.10. निम्नलिखित में सार्थक अंकों की संख्या लिखिए
(a) 0.007 m²
(b) 2.64 x 10²⁴ kg
(c) 0.2370 cm^-3
(d) 6.320 J
(e) 6.032 Nm^-2
(f) 0.0006032 m²

(a) 1
(b) 3
(e) 4
(d) 4
(e) 4
(f) 4

प्रश्न.11. धातु की किसी आयताकार शीट की लम्बाई, चौड़ाई व मोटाई क्रमशः 4,234 m, 1.005 m व 2.01 cm है। उचित सार्थक अंकों तक इस शीट का पृष्ठीय क्षेत्रफल व आयतन ज्ञात कीजिए।

यहाँ लम्बाई 4 = 4.234 m, चौड़ाई b =1.005 m

तथा मोटाई c = 2.01 cm = 0.0201 m

स्पष्ट है कि लम्बाई व चौड़ाई में 4-4 सार्थक अंक हैं जबकि मोटाई में 3 सार्थक अंक हैं।

∴ पृष्ठीय क्षेत्रफल तथा आयतन दोनों का अधिकतम 3 सार्थक अंकों में पूर्णांकन करना होगा।

अब शीट का पृष्ठीय क्षेत्रफल

= 2x (ab + bc + ca)

= 2x [4.234 x 1.005 + 1.005 x 0.0201 + 0.0201 x 4234] m²

= 2x [4.25517 + 0.0202005 + 0.0851034] m²

= 2 x 4.3604739 m = 8.7209478 m = 8.72 m²

जबकि शीट का आयतन = ल० x चौ० x ऊँ०

= 4.234 m x 1.005 m x 0.0201 m

= 0.085528917 m³

= 0.0855 m³

प्रश्न.12. पंसारी की तुला द्वारा मापे गए डिब्बे का द्रव्यमान 2.300 kg है। सोने के दो टुकड़े जिनका द्रव्यमान क्रमशः 20.15 g व 20.17 g है, डिब्बे में रखे जाते हैं
(a) डिब्बे का कुल द्रव्यमान कितना है,
(b) उचित सार्थक अंकों तक टुकड़ों के द्रव्यमानों में कितना अन्तर है?

(a) दिया है: डिब्बे का द्रव्यमान = 2300 kg
पहले टुकड़े का द्रव्यमान = 20.15 g = 0.02015 kg
दूसरे टुकड़े का द्रव्यमान = 2017 g= 0.02017 kg
∴ टुकड़े रखने के बाद डिब्बे का कुल द्रव्यमान
= 2.300 kg + 0.02015 kg + 0.02017kg
= 2.34032 kg
∵ तीनों मांपों में डिब्बे के द्रव्यमान में सबसे कम सार्थक अंक (4 अंक) हैं; अतः डिब्बे के कुल द्रव्यमान का अधिकतम चार सार्थक अंकों में पूर्णांकन करना होगा।
∴ डिब्बे का कुल द्रव्यमान = 2.340 kg
(b) ∵ सोने के टुकड़ों के द्रव्यमानों में प्रत्येक में 4 सार्थक अंक हैं; अतः इनके अन्तर का अधिकतम
दशमलव के दूसरे स्थान तक पूर्णांकन करना होगा।
टुकड़ों के द्रव्यमानों का अन्तर = 20.17 g – 20.16 g= 0.02 g

प्रश्न.13. कोई भौतिक राशि P, चार प्रेक्षण-योग्य राशियों a, b, c तथा d से इस प्रकार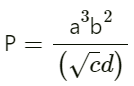

a, b, c तथा d के मापने में प्रतिशत त्रुटियाँ क्रमशः 1%, 3%, 4% तथा 2% हैं। राशि P में प्रतिशत त्रुटि कितनी है? यदि उपर्युक्त सम्बन्ध का उपयोग करके P का परिकलित मान 3. 763 आता है तो आप परिणाम का किस मान तक निकटन करेंगे?

∴ P के मान में प्रतिशत त्रुटि 

= 0.4891
= 0.489 (उचित सार्थक अंकों तक)
P के मान में त्रुटि 0.489 से स्पष्ट है कि P के मान में दशमलव  के पहले स्थान पर स्थित अंक ही संदिग्ध है; अत: P के मान को दशमलव के दूसरे स्थान तक लिखना व्यर्थ है। अतः P के मान का दशमलव के पहले स्थान तक पूर्णांकन करना होगा।
अतः P का निकटतम मान = 3.763 = 3.8

प्रश्न.14. किसी पुस्तक में, जिसमें छपाई की अनेक त्रुटियाँ हैं, आवर्त गति कर रहे किसी कण के विस्थापन के चार भिन्न सूत्र दिए गए हैं

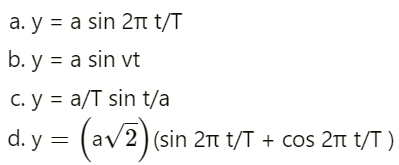
(a = कण का अधिकतम विस्थापन, ν = कण की चाल, T = गति का आवर्तकाल)।
विमीय आधारों पर गलत सूत्रों को निकाल दीजिए।

किसी त्रिकोणमितीय फलन का कोण एक विमाहीन राशि होती है।
सूत्र (b) तथा (c) में कोण vt तथा ! विमाहीन नहीं हैं; अत: उपर्युक्त दोनों सूत्र सही नहीं हैं। शेष दोनों सूत्र (a) तथा (d) सही हैं।

प्रश्न.15. भौतिकी का एक प्रसिद्ध संबंध किसी कण के चल द्रव्यमान (moving mass) m, 'विराम द्रव्यमान (rest mass) m₀', इसकी चाल ν और प्रकाश c की चाल के बीच है। (यह संबंध सबसे पहले अल्बर्ट आईंस्टाइन के विशेष आपेक्षिकता के सिद्धांत के परिणामस्वरूप उत्पन्न हुआ था।) कोई छात्र इस संबंध को लगभग सही याद करता है। लेकिन स्थिरांक c को लगाना भूल जाता है। वह लिखता है: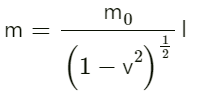  

अनुमान लगाइए कि c कहाँ लगेगा?

दिया गया संबंध है। 

इस संबंध का दायाँ पक्ष विमाहीन है ; अतः सूत्र के सही होने के लिए बायाँ पक्ष भी विमाहीन होना चाहिए जबकि ऐसा तभी हो पाएगा जबकि बायाँ पक्ष 

प्रश्न.16. परमाण्विक पैमाने पर लम्बाई का सुविधाजनक मात्रक ऍग्स्ट्रॉम है और इसे 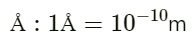 द्वारा निर्दिष्ट किया जाता है। हाइड्रोजन के परमाणु का आमाप लगभग  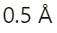है। हाइड्रोजन परमाणुओं के एक मोल का m’ में कुल आण्विक आयतन कितना होगा?

हाइड्रोजन परमाणु की त्रिज्या, rAr = 0.5A. = 0.5 × 10^-10 मीटर 

आवोगाद्रो की परिकल्पना से,
हाइड्रोजन के 1 मोल में परमाणुओं की संख्या
N = 6.023 × 10²³
हाइड्रोजन परमाणु के 1 मोल के परमाणुओं का आयतन
V = N × V
= 6.023 × 10²³ × 5.233 × 10^-31
= 3.15 × 10^-7 मी³ 

प्रश्न.17. किसी आदर्श गैस का एक मोल (ग्राम अणुक) मानक ताप व दाब पर 22.4L आयतन (ग्राम अणुक आयतन) घेरता है। हाइड्रोजन के ग्राम अणुक आयतन तथा उसके एक मोल के परमाण्विक आयतन का अनुपात क्या है? (हाइड्रोजन के (की आमाप लगभग 1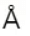 मानिए)। यह अनुपात इतनी अधिक क्यों है?

एक मोल हाइड्रोजन गैस का आयतन = 22.4
L =22.4 x 10^-3 m³
जबकि 1 मोल हाइड्रोजन गैस का परमाण्विक आयतन =3.15 x 10^-7 m³ 

अतः अभीष्ट अनुपात 7.11 × 10⁴ : 1 है।
इसे अनुपात का मान इतना अधिक होने का अर्थ है कि गैस का आयतन उसमें उपस्थित अणुओं के वास्तविक आयतन की तुलना में बहुत अधिक होता है। इसका अन्य अर्थ यह है कि गैस के अणुओं के बीच बहुत अधिक खाली स्थान होता है।

प्रश्न.18. इस सामान्य प्रेक्षण की स्पष्ट व्याख्या कीजिए : यदि आप तीव्र गति से गतिमान किसी रेलगाड़ी की खिड़की से बाहर देखें तो समीप के पेड़, मकान आदि रेलगाड़ी की गति की विपरीत दिशा में तेजी से गति करते प्रतीत होते हैं, परन्तु दूरस्थ पिण्ड (पहाड़ियाँ, चन्द्रमा, तारे आदि) स्थिर प्रतीत होते हैं। (वास्तव में क्योंकि आपको ज्ञात है कि आप चल रहे हैं, इसलिए ये दूरस्थ वस्तुएँ आपको अपने साथ चलती हुई प्रतीत होती हैं।)

किसी वस्तु का हमारे सापेक्ष गति करते हुए प्रतीत होना, हमारे सापेक्ष वस्तु के कोणीय वेग पर निर्भर करता है न कि उसके रेखीय वेग पर। यद्यपि गाड़ी से यात्रा करते समय सभी वस्तुएँ समान वेग से हमारे पीछे की ओर गति करती हैं, परन्तु समीप स्थित वस्तुओं का हमारे सापेक्ष कोणीय वेग अधिक होता है; अतः वे तेजी से पीछे जाती प्रतीत होती हैं जबकि दूर स्थित वस्तुओं का हमारे सापेक्ष कोणीय वेग बहुत ही कम होता है; अतः वे हमें लगभग स्थिर प्रतीत होती हैं।

प्रश्न.19. समीपी तारों की दूरियाँ ज्ञात करने के लिए लम्बन के सिद्धान्त का प्रयोग किया जाता है। सूर्य के परितः अपनी कक्षा में छः महीनों के अन्तराल पर पृथ्वी की अपनी, दो स्थानों को मिलाने वाली, आधार रेखा AB है। अर्थात आधार रेखा पृथ्वी की कक्षा के व्यास ≈ 3 x 10¹¹ m के लगभग बराबर है। लेकिन चूंकि निकटतम तारे भी इतने अधिक दूर हैं। कि इतनी लम्बी आधार रेखा होने पर भी वे चाप के केवल 1″ (सेकण्ड, चाप का) की कोटि का लम्बन प्रदर्शित करते हैं। खगोलीय पैमाने पर लम्बाई का सुविधाजनक मात्रक पारसेक है। यह किसी पिण्ड की वह दूरी है जो पृथ्वी से सूर्य तक की दूरी के बराबर आधार रेखा के दो विपरीत किनारों से चाप के 1′ का लम्बन प्रदर्शित करती है। मीटरों में एक पारसेक कितना होता है?

प्रश्न.20. हमारे सौर परिवार से निकटतम तारा 4.29 प्रकाश वर्ष दूर है। पारसेक में यह दूरी कितनी है? यह तारा (ऐल्फा सेटौरी नामक) तब कितना लम्बन प्रदर्शित करेगा जब इसे सूर्य के परितः अपनी कक्षा में पृथ्वी के दो स्थानों से जो छः महीने के अन्तराल पर हैं, देखा, जाएगा?

प्रश्न.21. भौतिक राशियों का परिशुद्ध मापन विज्ञान की आवश्यकताएँ हैं। उदाहरण के लिए, किसी शत्रु के लड़ाकू जहाज की चाल सुनिश्चित करने के लिए बहुत ही छोटे समयान्तरालों पर इसकी स्थिति का पता लगाने की कोई यथार्थ विधि होनी चाहिए। द्वितीय विश्वयुद्ध में रेडार की खोज के पीछे वास्तविक प्रयोजन यही था। आधुनिक विज्ञानं के उन भिन्न उदाहरणों को सोचिए जिनमें लम्बाई, समय, द्रव्यमान आदि के परिशुद्ध मापन की आवश्यकता होती है। अन्य जिस किसी विषय में भी आप बता सकते हैं, परिशुद्धता की मात्रात्मक धारणा दीजिए।

• लम्बाई का मापन: विभिन्न यौगिकों के क्रिस्टलों में परमाणुओं के बीच की दूरी का मापन करते समय लम्बाई के परिशुद्ध मापन की आवश्यकता होती है।
• समय का मापन: फोको की विधि द्वारा किसी माध्यम में प्रकाश की चाल ज्ञात करने के प्रयोग में समय के परिशुद्ध मापन की आवश्यकता होती है।
• द्रव्यमान का मापन: द्रव्यमान स्पेक्ट्रमलेखी में परमाणुओं के द्रव्यमान का परिशुद्ध मापन किया जाता है।

प्रश्न.22. जिस प्रकार विज्ञान में परिशुद्ध मापन आवश्यक है, उसी प्रकार अल्पविकसित विचारों तथा सामान्य प्रेक्षणों को उपयोग करने वाली राशियों के स्थूल आकलन कर सकना भी उतना ही महत्त्वपूर्ण है। उन उपायों को सोचिए जिनके द्वारा आप निम्नलिखित का अनुमान लगा सकते हैं-(जहाँ अनुमान लगाना कठिन है वहाँ राशि की उपरिसीमा पता लगाने का प्रयास कीजिए)
(a) मानसून की अवधि में भारत के ऊपर वर्षाधारी मेघों का कुल द्रव्यमान।
(b) किसी हाथी का द्रव्यमान।
(c) किसी तूफान की अवधि में वायु की चाल।
(d) आपके सिर के बालों की संख्या।
(e) आपकी कक्षा के कमरे में वायु के अणुओं की संख्या।

(a) सर्वप्रथम मौसम विभाग से पूरे भारत में हुई कुल वर्षा की माप की जानकारी लेंगे और वर्षा जल के आयतन को जल के घनत्व से गुणा करके वर्षा जल के द्रव्यमान की गणना कर लेंगे। इससे मेघों का द्रव्यमान ज्ञात हो जाएगा।
(b) ट्रक आदि का द्रव्यमान मापने वाले काँटे पर खड़ा करके हाथी को द्रव्यमान ज्ञात किया जा सकता है।
(c) किसी तूफान की अवधि में वायु द्वारा उत्पन्न दाब को मापकर, वायु की चाल का आकलन किया जा सकता है।
(d) सिर के 1cm² क्षेत्रफल में स्थित बालों को गिन लिया जाएगा। तत्पश्चात् सिर के क्षेत्रफल का आकलन करके इस क्षेत्रफल से 1cm² क्षेत्रफल में स्थित बालों की संख्या को गुणा करके सिर के बालों की संख्या का आकलन किया जा सकता है।
(e) कक्षा के कमरे में उपस्थित वायु का घनत्व नापकर 1cm³ आयतन में उपस्थित अणुओं की संख्या की गणना की जा सकती है। तत्पश्चात् कमरे के आयतन से गुणा करके कक्षा के कमरे में उपस्थित वायु के अणुओं की गणना की जा सकती है।

प्रश्न.23. सूर्य एक ऊष्म प्लैज्मा (आयनीकृत पदार्थ) है जिसके आन्तरिक क्रोड का ताप 10⁷K से अधिक और बाह्य पृष्ठ का ताप लगभग 6000 K है। इतने अधिक ताप पर कोई भी पदार्थ ठोस या तरल प्रावस्था में नहीं रह सकता। आपको सूर्य का द्रव्यमान घनत्व किस परिसर में होने की आशा है? क्या यह ठोसों, तरलों या गैसों के घनत्वों के परिसर में है? क्या आपका अनुमान सही है, इसकी जाँच आप निम्नलिखित आँकड़ों के आधार पर कर सकते हैं- सूर्य का द्रव्यमान = 2.0 × 10³⁰ kg सूर्य की त्रिज्या = 7.0 x 10⁸ m.

प्रश्न.24. जब बृहस्पति ग्रह पृथ्वी से 8247 लाख किलोमीटर दूर होता है तो इसके व्यास की कोणीय माप 35.72′ का चाप है। बृहस्पति का व्यास परिकलित कीजिए।

दिया है, बृहस्पति ग्रह की पृथ्वी से दूरी

s = 8247 लाख किलोमीटर = 8247 x 10⁵ किमी
= 1.43 × 10⁵ किमी
= 1.43 × 10⁸ किमी