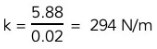Force-Extension Graphs | Physics for Grade 10 PDF Download

Clear all your Grade 10 doubts with EduRev Join for Free

Join for Free

Linear & Non-Linear Extension

• Hooke’s law is the linear relationship between force and extension
  • This is represented by a straight line on a force-extension graph
• Materials that do not obey Hooke's law, i.e they do not return to their original shape once the force has been removed, have a non-linear relationship between force and extension
  • This is represented by a curve on a force-extension graph
• Any material beyond its limit of proportionality will have a non-linear relationship between force and extension
  
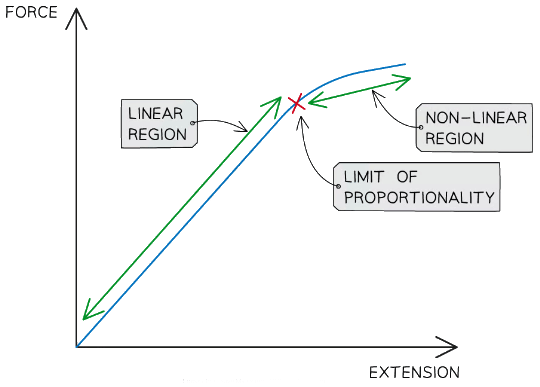  Linear and non-linear regions of a force-extension graph

Calculating Spring Constant

• The spring constant can be calculated by rearranging the Hooke's law equation for k:
  k = F/e
• Where:
  • k = spring constant in newtons per metres (N/m)
  • F = force in newtons (N)
  • e = extension in metres (m)
• This equation shows that the spring constant is equal to the force per unit extension needed to extend the spring, assuming that its limit of proportionality is not reached
• The stiffer the spring, the greater the spring constant and vice versa

  • This means that more force is required per metre of extension compared to a less stiff spring
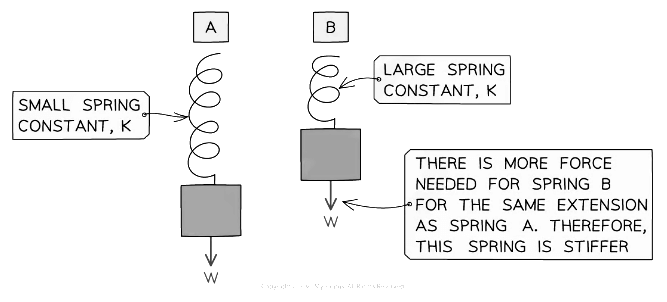    A spring with a larger spring constant needs more force per unit extension (it is stiffer)

• The spring constant is also used in the equation for elastic potential energy

Tip: Remember the unit for the spring constant is Newtons per metres (N/m). This is commonly forgotten in exam questions

Example: A mass of 0.6 kg is suspended from a spring, where it extends by 2 cm. Calculate the spring constant of the spring.

Step 1: List the known quantities
Mass, m = 0.6 kg
Extension, e = 2 cm

Step 2: Write down the relevant equation
k = F/e

Step 3: Calculate the force
The force on the spring is the weight of the mass
g is Earth's gravitational field strength (9.8 N/kg)
W = mg = 0.6 × 9.8 = 5.88 N

Step 4: Convert any units
The extension must be in metres
2 cm = 0.02 m

Step 5: Substitute values into the equation

Interpreting Graphs of Force v Extension

• The relationship between force and extension is shown on a force-extension graph
• If the force-extension graph is a straight line, then the material obeys Hooke's law
  • Sometimes, this may only be a small region of the graph, up to the material's limit of proportionality
    
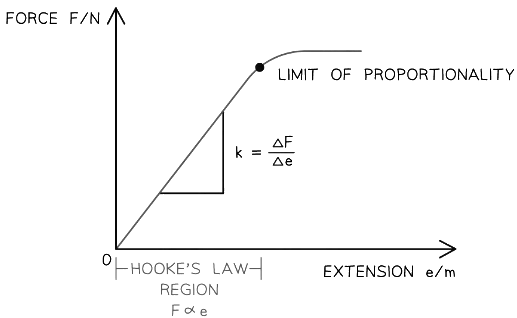    The Hooke's law region on a force-extension graph is where the graph is a straight line
• The symbol Δ means the 'change in' a variables
  • For example, ΔF and Δe are the 'change in' force and extension respectively
  • This is the same as rise ÷ run for calculating the gradient
• The '∝' symbol means 'proportional to'
  • i.e. F ∝ e means the 'the force is proportional to the extension'
    
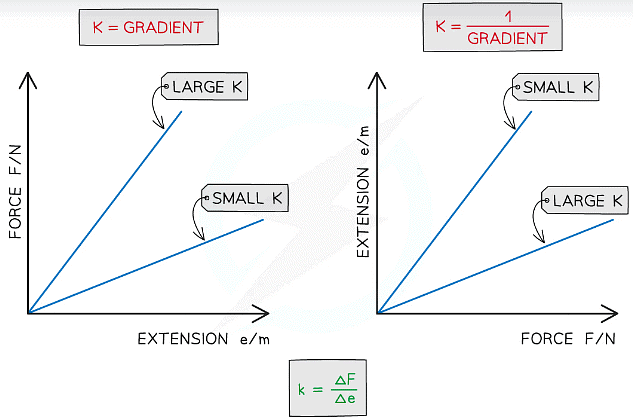    The spring constant is the gradient, or 1 ÷ gradient of a force-extension graph depending on which variable is on which axis 
• If the force is on the y axis and the extension on the x axis, the spring constant is the gradient of the straight line (Hooke's law) region of the graph
  • If the graph has a steep straight line, this means the material has a large spring constant
  • If the graph has a shallow straight line, this means the material has a small spring constant
• If the force is on the x axis and the extension on the y axis, the spring constant is 1 ÷ gradient of the straight line (Hooke's law) region of the graph
  • If the graph has a steep straight line, this means the material has a small spring constant
  • If the graph has a steep straight line, this means the material has a large spring constant

Tip:  Make sure to always check which variables are on which axes to determine which line has a larger or smaller spring constant, as well as the units for calculations

Question for Force-Extension Graphs

Try yourself:A student investigates the relationship between the force applied and extension for three springs K, L and M. The results are shown on the graph below:

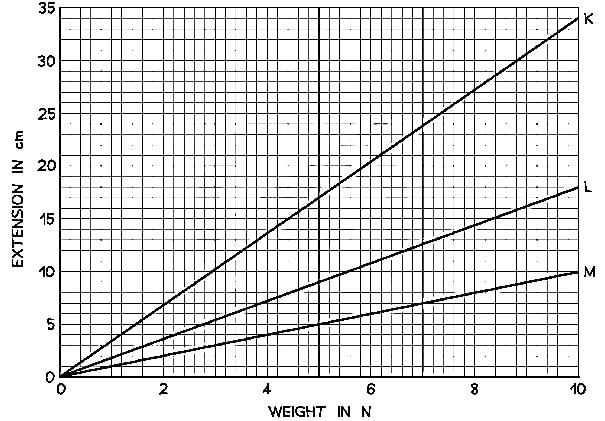
Which of the statements is correct?

• A.

  K has a higher spring constant than the other two springs
• B.

  M has the same spring constant as K
• C.

  L has a higher spring constant than M
• D.

  K has a lower spring constant than the other two springs

Explanation

• The graph has the extension on the y axis and the weight (force) on the x-axis
  • This means that the spring constant is 1 ÷ gradient
• Therefore the steeper the straight line, the lower the spring constant
• K has the steepest gradient and therefore has a lower spring constant than L and M

Report a problem

Cancel Report

View Solution