Moments & their Principle | Physics for Grade 10 PDF Download
| Table of contents |

|
| Forces & Rotation |

|
| The Moment of a Force |

|
| The Principle of Moments |

|
| Solved Example |

|
Forces & Rotation
- As well as causing objects to speed up, slow down, change direction and deform, forces can also cause objects to rotate
- A system of forces can also do this
- An example of a rotation caused by a force is on one side of a pivot (a fixed point that the object can rotate around)
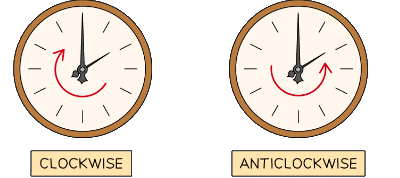
- This rotation can be clockwise or anticlockwise
 The force will cause the object to rotate clockwise about the pivot
The force will cause the object to rotate clockwise about the pivot
- This rotation can be clockwise or anticlockwise
- More examples of rotation caused by a force are:
- A child on a see-saw
- Turning the handle of a spanner
- A door opening and closing
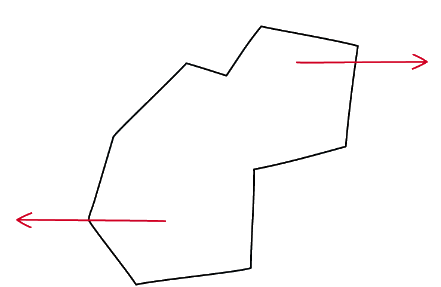
If two forces act on an object without passing through the same point, then the object can still rotate
If the forces are equal and opposite, this is known as a couple
 The above forces are balanced, but will still cause the object to rotate clockwise as they don’t act through a common point
The above forces are balanced, but will still cause the object to rotate clockwise as they don’t act through a common point
The Moment of a Force
- A moment is defined as:
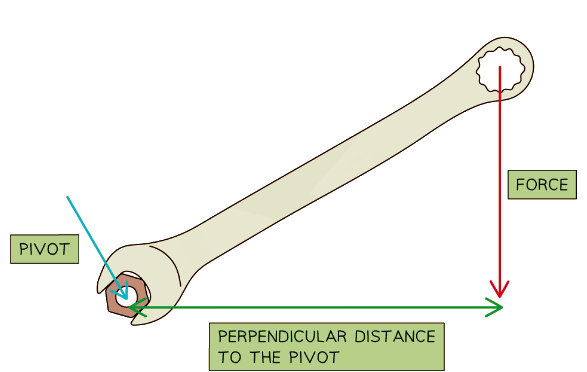
The turning effect of a force about a pivot - The size of a moment is defined by the equation:
- M = F × d
- Where:
- M = moment in newton metres (Nm)
- F = force in newtons (N)
- d = perpendicular distance of the force to the pivot in metres (m)

- This is why, for example, the door handle is placed on the opposite side to the hinge
- This means for a given force, the perpendicular distance from the pivot (the hinge) is larger
- This creates a larger moment (turning effect) to make it easier to open the door
- Opening a door with a handle close to the pivot would be much harder, and would require a lot more force
Tip: The units of a moment is Newton metres (N m), but can also be Newton centimetres (N cm) ie. where the distance is measured in cm insteadIf the exam question doesn't ask for a specific unit, always convert the distance into metres
The Principle of Moments
- The principle of moments states that:
If an object is balanced, the total clockwise moment about a pivot equals the total anticlockwise moment about that pivot - Remember that the moment = force × distance from a pivot
- The forces should be perpendicular to the distance from the pivot
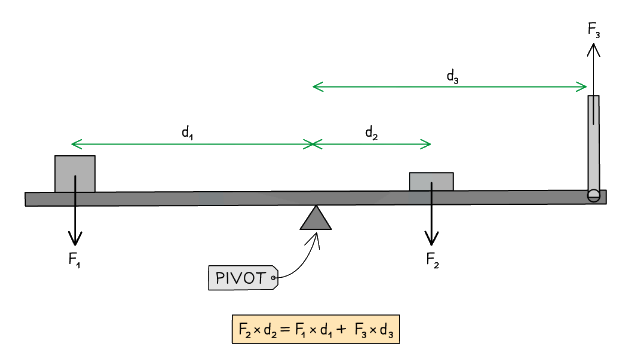
- For example, on a horizontal beam, the forces which will cause a moment are those directed upwards or downwards
 Moments on a balanced beam
Moments on a balanced beam
- For example, on a horizontal beam, the forces which will cause a moment are those directed upwards or downwards
- In the above diagram:
- Force F2 is supplying a clockwise moment;
- Forces F1 and F3 are supplying anticlockwise moments
- Due to the principle of moments, if the beam is balanced
Total clockwise moments = Total anticlockwise moments - Hence:
F2 × d2 = (F1 × d1) + (F3 × d3)
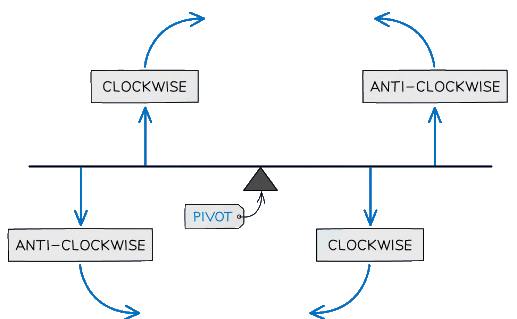
Tip: Make sure that all the distances are in the same units and you’re considering the correct forces as clockwise or anticlockwise, as seen in the diagram below
Clockwise is defined as the direction the hands of a clock move (and anticlockwise as the opposite)
 |
Download the notes
Moments & their Principle
|
Download as PDF |
Solved Example
Example: A parent and child are at opposite ends of a playground see-saw. The parent weighs 690 N and the child weighs 140 N. The adult sits 0.3 m from the pivot. Calculate the distance the child must sit from the pivot for the see-saw to be balanced.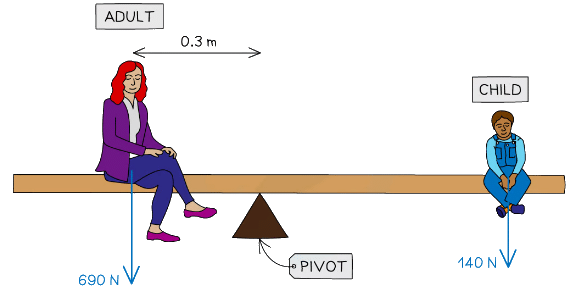
Step 1: List the know quantities
Clockwise force (child), Fchild = 140 N
Anticlockwise force (adult), Fadult = 690 N
Distance of adult from the pivot, dadult = 0.3 mStep 2: Write down the relevant equation
Moment = force × distance from pivot
For the see-saw to balance, the principle of moments states that
Total clockwise moments = Total anticlockwise momentsStep 3: Calculate the total clockwise moments
The clockwise moment is from the child
Momentchild = Fchild × dchild = 140 × dchildStep 4: Calculate the total anticlockwise moments
The anticlockwise moment is from the adult
Momentadult = Fadult × dadult = 690 × 0.3 = 207 NmStep 5: Substitute into the principle of moments equation
140 × dchild = 207Step 6: Rearrange for the distance of the child from the pivot
dchild = 207 ÷ 140 = 1.48 m
|
124 videos|149 docs|37 tests
|

 Clockwise is defined as the direction the hands of a clock move (and anticlockwise as the opposite)
Clockwise is defined as the direction the hands of a clock move (and anticlockwise as the opposite)