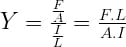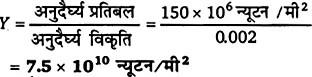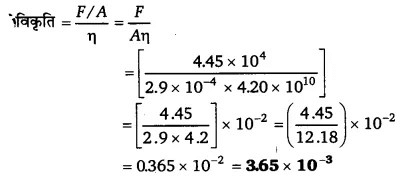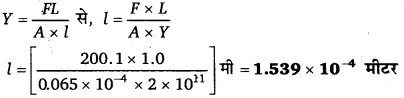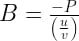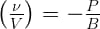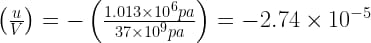ठोसों के यांत्रिक गुण (Mechanical Properties of Solids) NCERT Solutions | NCERT Textbooks in Hindi (Class 6 to Class 12) - UPSC PDF Download

अभ्यास

प्रश्न.1. 4.7 m लम्बे व 3.0 x 10^-5 m² अनुप्रस्थ काट के स्टील के तार तथा 3.5 m लम्बे व 40 x 10^-5m² अनुप्रस्थ काट के ताँबे के तार पर दिए गए समान परिमाण के भारों को लटकाने पर उनकी लम्बाइयों में समान वृद्धि होती है। स्टील तथा ताँबे के यंग-प्रत्यास्थता गुणांकों में क्या अनुपात है?

यंग-प्रत्यास्थता गुणांक 

यहाँ दोनों तारों के लिए लटकाया गया भार F = Mg तथा लम्बाई में वृद्धि l समान है, अतः Y∝(L/A)

प्रश्न 2. चित्र-9.1 में किसी दिए गए पदार्थ के लिए प्रतिबल-विकृति वक्र दर्शाया गया है। इस पदार्थ के लिए
(a) यंग-प्रत्यास्थता गुणांक, तथा
(b) सन्निकट पराभव सामर्थ्य क्या है?

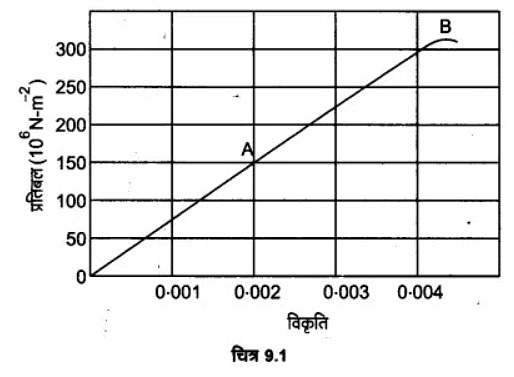
(a) ग्राफ के सरल रेखीय भाग में बिन्दु A के संगत

अनुदैर्ध्य प्रतिबल = 150 × 10⁶ न्यूटन/मी

तथा अनुदैर्घ्य विकृति = 0.002

∴ यंग-प्रत्यास्थता गुणांक

(b) पराभव बिन्दु लगभग B है।

अत: इसके संगत पदार्थ की पराभव सामर्थ्य = 300 × 10⁶ न्यूटन/मीटर

= 300 × 10⁸ न्यूटन/मी

प्रश्न.3. दो पदार्थों A और B के लिए प्रतिबल-विकृति ग्राफ चित्र-9.2 में दर्शाए गए हैं।

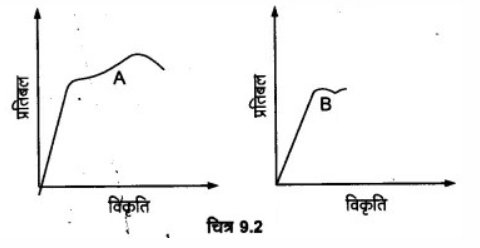इन ग्राफों को एक ही पैमाना मानकर खींचा गया है।
(a) किस पदार्थ का यंग प्रत्यास्थता गुणांक अधिक है?
(b) दोनों पदार्थों में कौन अधिक मजबूत है?

(a) ∵ पदार्थ A के ग्राफ का ढाल दूसरे ग्राफ की तुलना में अधिक है; अतः पदार्थ A का यंग गुणांक अधिक है।
(b) दोनों ग्राफों पर पराभव बिन्दुओं की ऊँचाई लगभग बराबर है परन्तु पदार्थ A के ग्राफ में पदार्थ B की तुलना में प्लास्टिक क्षेत्र अधिक सुस्पष्ट है; अतः पदार्थ A अधिक मजबूत है।

प्रश्न.4. निम्नलिखित दो कथनों को ध्यान से पढिए और कारण सहित बताइए कि वे सत्य हैं या असत्य
(a) इस्पात की अपेक्षा रबड़ का यंग गुणांक अधिक है;
(b) किसी कुण्डली का तनन उसके अपरूपण गुणांक से निर्धारित होता है।

(a) असत्य, रबड़ तथा इस्पात के बने एक जैसे तारों में समान विकृति उत्पन्न करने के लिए इस्पात के तार में रबड़ के तार की अपेक्षा अधिक प्रतिबल उत्पन्न होता है, इससे स्पष्ट है कि इस्पात का यंग गुणांक रबड़ की अपेक्षा अधिक है।
(b) सत्य, जब हम किसी कुण्डली (स्प्रिग) को खींचते हैं तो न तो स्प्रिंग निर्माण में लगे तार की लम्बाई में कोई परिवर्तन होता है और न ही उसके आयतन में। केवल स्प्रिंग का रूप बदल जाता है; अतः स्प्रिंग का तनन उसके अपरूपण गुणांक द्वारा निर्धारित होता है।

प्रश्न.5. 0.25 cm व्यास के दो तार, जिनमें एक इस्पात का तथा दूसरा पीतल का है, चित्र-9.3 के अनुसार भारित हैं। बिना भार लटकाए इस्पात तथा पीतल के तारों की लम्बाइयाँ क्रमशः स्टील 1.5 m तथा 1.0m हैं। यदि इस्पात तथा पीतल के यंग गुणांक क्रमशः 20 x 10¹¹ Pa तथा 0.91 × 10¹¹ Pa हों तो इस्पात तथा पीतल के तारों में विस्तार की गणना कीजिए।

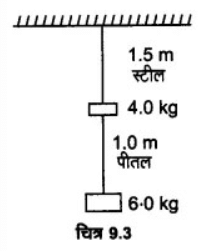
यहाँ स्टील के तार के लिए

त्रिज्या  r₁ = (0.25/2) सेमी = 0.125 सेमी

= 0.125 x 10^-2 मी

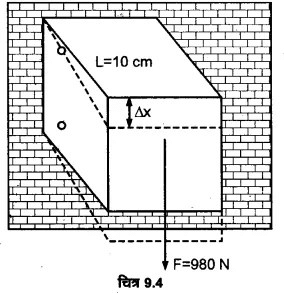
प्रश्न.6. ऐलुमिनियम के किसी घन के किनारे 10 cm लम्बे हैं। इसकी एक फलक किसी ऊर्ध्वाधर दीवार से कसकर जड़ी हुई है। इस घन के सम्मुख फलक से 100 kg का एक द्रव्यमान जोड़ दिया गया है। ऐलुमिनियम का अपरूपण गुणांक 25 GPa है। इस फलक का ऊध्र्वाधर विस्थापन कितना होगा?

दिया है: अपरूपण गुणांक  G = 25 GPa = 25 x 10⁹ Nm^-2

बल-आरोपित फलक का क्षेत्रफल A = 10 cm x 10 cm = 100 x 10^-4 m²

प्रश्न.7. मृदु इस्पात के चार समरूप खोखले बेलनाकार स्तम्भ 50,000 kg द्रव्यमान के किसी बड़े ढाँचे को आधार दिए हुए हैं। प्रत्येक स्तम्भ की भीतरी तथा बाहरी त्रिज्याएँ क्रमशः 30 तथा 60 cm हैं। भार वितरण को एकसमान मानते हुए प्रत्येक स्तम्भ की सम्पीडन विकृति की गणना कीजिए।

दिया है: बाहरी त्रिज्या R_ext = 60 cm = 0.6 m

भीतरी त्रिज्या R_int = 30 cm = 0.3 m

∴ प्रत्येक स्तम्भ का अनुप्रस्थ क्षेत्रफल

प्रश्न 8. ताँबे का एक टुकड़ा, जिसका अनुप्रस्थ परिच्छेद 15.2 mm x 19.1 mm का है, 44,500 N बल के तनाव से खींचा जाता है, जिससे केवल प्रत्यास्थ विरूपण उत्पन्न हो। उत्पन्न विकृति की गणना कीजिए।

विरूपण विकृति से संगत प्रत्यास्थता गुणांक अपरूपण गुणांक (दृढ़ता गुणांक η होता है जो यहाँ 4.20 x 10¹⁰ Pa) दिया है।

ताँबे के टुकड़े का अनुप्रस्थ-परिच्छेद

A = (15.2 x 10^-3 मी) x (19.1 x 10^-3 मी)
= 290.32 x 10^-6 मी² = 2.9 x 10^-4 मी²
विरूपक बल F =44500 न्यूटन = 4.45 x 10⁴ न्यूटन

प्रश्न.9. 1.5 cm त्रिज्या का एक इस्पात का केबिल भार उठाने के लिए इस्तेमाल किया जाता है। | यदि इस्पात के लिए अधिकतम अनुज्ञेय प्रतिबल 108 Nm^-2 है तो उस अधिकतम भार की गणना कीजिए जिसे केबिल उठा सकता है।

केबिल के अनुप्रस्थ-परिच्छेद का क्षेत्रफल ।
A = πr² = 3.14 x (1.5 x 10^-2 मी )² = 7.065 x 10^-4 मी²
अधिकतम अनुज्ञेय प्रतिबल = 108 न्यूटन/मीटर2
∴ बल F = (F/A) x A = प्रतिबल x अनुप्रस्थ-काट का क्षेत्रफल
∴ केबिल द्वारा उठाया जा सकने वाला अधिकतम भार ।
= अनुज्ञेय प्रतिबल x अनुप्रस्थ-काट को क्षेत्रफल
= (108 न्यूटन /मी²) x (7.065 x 10^-4 मी²)
= 7.065 x 10⁴ न्यूटन = 7.07 x 10⁴ न्यूटन

प्रश्न.10. 15 kg द्रव्यमान की एक दृढ़ पट्टी को तीन तारों, जिनमें से प्रत्येक की लम्बाई 2 m है, से सममित लटकाया गया है। सिरों के दोनों तार ताँबे के हैं तथा बीच वाली तार लोहे का है। तारों के व्यासों के अनुपात ज्ञात कीजिए जबकि प्रत्येक पर तनाव उतना ही रहता है।

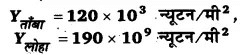
प्रत्येक तार द्वारा सम्भाला जाने वाला भार

प्रश्न 11. एक मीटर अतानित लम्बाई के इस्पात के तार के एक सिरे से 14.5 kg का द्रव्यमान बाँध कर उसे एक ऊर्ध्वाधर वृत्त में घुमाया जाता है, वृत्त की तली पर उसका कोणीय वेग 2 rev/s है। तार के अनुप्रस्थ परिच्छेद का क्षेत्रफल 0.065cm² है। तार में विस्तार की गणना कीजिए जब द्रव्यमान अपने पथ के निम्नतम बिन्दु पर है। (इस्पात के लिए Y = 2 × 10¹¹ न्यूटन/मी²)

ऊध्र्वाधर वृत्त के निम्नतम बिन्दु पर

F – mg = mrω²
डोरी में तनाव बल F = mrω² + mg
F = [14.5 x 1.0 x (2.0)² + 14.5 x 9.8] न्यूटन
= [58.0 + 142.1] न्यूटन = 200.1 न्यूटन
तथा L = 1.00 मी, अनुप्रस्थ-काट A = 0.065 सेमी² = 0.065 x 10^-4 मी² तथा
Y = 2 x 10¹¹ न्यूटन/मी²

सूत्र

प्रश्न.12. नीचे दिए गए आँकड़ों से जल के आयतन प्रत्यास्थता गुणांक की गणना कीजिए; प्रारम्भिक आयतन = 100.0, दाब में वृद्धि = 100.0 atm (1 atm = 1.013 x 10⁵ Pa), अन्तिम आयतन = 100.5 L नियत ताप पर जल तथा वायु के आयतन प्रत्यास्थता गुणांकों की तुलना कीजिए। सरल शब्दों में समझाइए कि यह अनुपात इतना अधिक क्यों है?

यहाँ प्रारम्भिक आयतन V = 100.0 लीटर

अन्तिम आयतन (V – υ) = 100.5 लीटर

आयतन में कमी υ = (V – υ) – (V) = 100 लीटर – 100.5 लीटर = – 0.5 लीटर

दाब में वृद्धि p = 100 वायुमण्डलीय दाब ।

= 100 x 1.013 x 10⁵ न्यूटन/मी²
= 1.013 x 10⁷ न्यूटन/मी

आयतन प्रत्यास्थता गुणांक

हम जानते हैं कि STP पर वायु का आयतन प्रत्यास्थता गुणांक 1 x 10⁵ Pa है, अतः जल का आयतन । प्रत्यास्थता गुणांक वायु के आयतन प्रत्यास्थता गुणांक से अधिक है। इसका कारण है कि समान दाब द्वारा जल के आयतन में होने वाली कमी, वायु के आयतन में होने वाली कमी की तुलना में नगण्य है।

प्रश्न.13. जल का घनत्व उस गंहराई पर, जहाँ दाब 80.0 atm हो, कितना होगा? दिया गया है कि | पृष्ठ पर जल का घनत्व 10³ x 10 kg³ m^-3, जल की सम्पीड्यता 45.8 x 10^-11 Pa^-1(1 Pa = 1Nm^-2)

यहाँ पृष्ठ से गहराई तक जाने पर दाब परिवर्तन p = (80.0 - 1.0) वायुमण्डल = 79वायुमण्डल अर्थात् ।

p = 79 x 1.013 x 10⁵ न्यूटन/मी²
= 80.027 x 10⁵ न्यूटन/मी²
जहाँ जल की संपीड्यता K = 45.8 x 10^-11 Pa^-1

जल को आयतन प्रत्यास्थता गुणांक

पृष्ठ पर जल का घनत्व ρ = 1.03 x 10³ kg m^-3

माना ρ’ किसी दी गई गहराई पर जल का घनत्व है। यदि V तथा  V’ जल के निश्चित द्रव्यमान M के पृष्ठ तथा दी गई गहराई के आयतन हैं तो

प्रश्न.14. काँच के स्लेब पर 10 atm का जलीय दाब लगाने पर उसके आयतन में भिन्नात्मक अन्तर की गणना कीजिए।

यहाँ दाब-परिवर्तन p = 10 वायुमण्डलीय दाब

= 10 x 1.013 x 10⁵ Pa = 1.013 x 10⁶ Pa
आयतन प्रत्यास्थता गुणांक B = 37 x 10⁹ Pa

आयतन प्रत्यास्थता गुणांक 

आयतन में भिन्नात्मक परिवर्त 

यहाँ (-) चिह्न आयतन में कमी का प्रतीक है।

प्रश्न.15. ताँबे के एक ठोस धन का एक किनारा 10 cm का है। इस पर 7.0 x 106 Pa.का.जलीय दाब लगाने पर इसके आयतन में संकुचन निकालिए।

आयतन विकृति

परन्तु घन के किनारे की लम्बाई a = 10 सेमी = 0.10 मी

घन का आयतन 20 = a³ = (0.10 मी) 3 = 10^-3 मी

अतः आयतन में परिवर्तन ) = आयतन विकृति x आयतन

= – 5 × 10^-5 x 10^-3 मी

=-5 × 10^-8 x 106 सेमी

=-0.05 सेमी

(-) चिह्न आयतन में संकुचन का प्रतीक है।

प्रश्न.16. 1 लीटर जल पर दाब में कितना अन्तर किया जाए कि वह 0.10% से सम्पीडित हो जाए?

यहाँ आयतन में प्रतिशत संकुचन = – 0.10

अर्थात् दाब 2.2 x 10⁶ Pa बढ़ाया जाये।