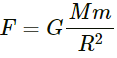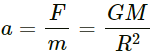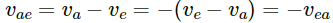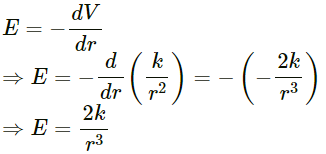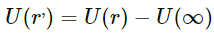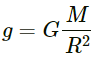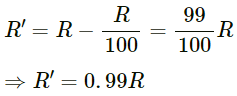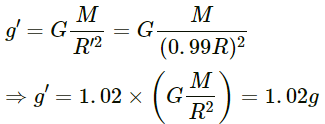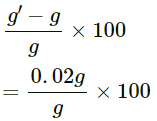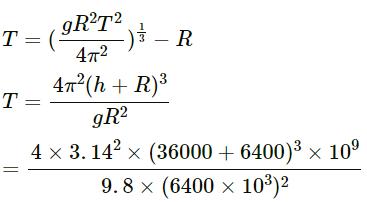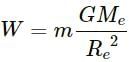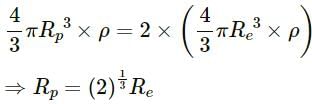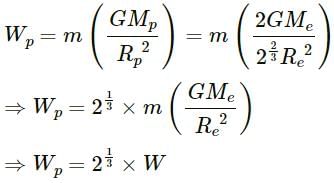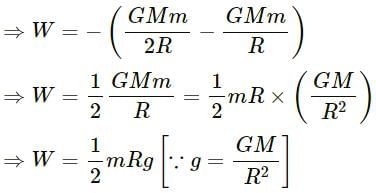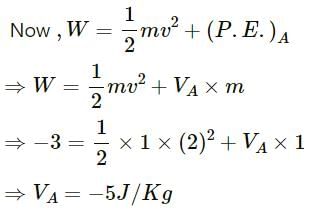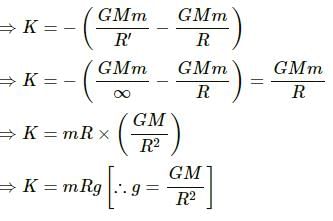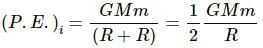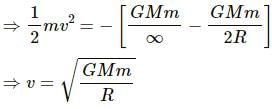HC Verma Questions and Solutions: Chapter 11: Gravitation- 1 | HC Verma Solutions - JEE PDF Download
Short Answers
Q.1. Can two particles be in equilibrium under the action of their mutual gravitational force? Can three particles be? Can one of the three particles be?
A particle will be in equilibrium when the net force acting on it is equal to zero. Two particles under the action of their mutual gravitational force will be in equilibrium when they revolve around a common point under the influence of their mutual gravitational force of attraction. In this case, the gravitational pull is used up in providing the necessary centripetal force. Hence, the net force on the particles is zero and they are in equilibrium. This is also true for a three particle system.
Q.2. Is there any meaning of "Weight of the earth"?
Weight of a body is always because of its gravitational attraction with earth. As law of gravitational attraction is universal so it applies to any two bodies (earth and sun as well).So we can define the weight of earth w.r.t a body of mass comparable or heavier than earth because of its gravitational attraction between earth and that body.
But practically no body on earth has mass comparable to earth so weight of earth will be a meaningless concept w.r.t earth frame.
Q.3. If heavier bodies are attracted more strongly by the earth, why don't they fall faster than the lighter bodies?
We know that acceleration due to a force on a body of mass in given by a = F/m. If F is the gravitational force acting on a body of mass m, then a is the acceleration of a free falling body.
This force is given as
Here, M is the mass of the Earth; G is the universal gravitational constant and R is the radius of the Earth.
∴ Acceleration due to gravity,
From the above relation, we can see that acceleration produced in a body does not depend on the mass of the body. So, acceleration due to gravity is the same for all bodies.
Q.4. Can you think of two particles which do not exert gravitational force on each other?
No. All practicals which have mass exert gravitational force on each other. Even massless particles experience the same gravitational force like other particles, because they do have relativistic mass.
Q.5. The earth revolves round the sun because the sun attracts the earth. The sun also attracts the moon and this force is about twice as large as the attraction of the earth on the moon. Why does the moon not revolve round the sun? Or does it?
We know that the Earth-Moon system revolves around the Sun. The gravitational force of the Sun on the system provides the centripetal force its revolution. Therefore, the net force on the system is zero and the Moon does not experience any force from the Sun. This is the reason why the Moon revolves around the Earth and not around the Sun.
Q.6. At noon, the sun and the earth pull the objects on the earth's surface in opposite directions. At midnight, the sun and the earth pull these objects in same direction. Is the weight of an object, as measured by a spring balance on the earth's surface, more at midnight as compared to its weight at noon?
No. Due to the revolution of the Earth around the Sun, the gravitational force of the Sun on the Earth system is almost zero. Hence, the body will not experience any force due to the Sun. Therefore, weight of the object will remain the same.
Q.7. An apple falls from a tree. An insect in the apple finds that the earth is falling towards it with an acceleration g. Who exerts the force needed to accelerate the earth with this acceleration g?
The mutual gravitational force between the apple and the Earth is responsible for the acceleration produced in the apple falling from the tree. Although the Earth will experience the same force, it does not get attracted towards the apple because of its large mass. The insect feels that the Earth is falling towards the apple with an acceleration g because of the the relative motion.
let
vae = velocity of apple w.r.t earth
Vea = velocity of earth w . r . t apple
As the insect is in the frame of apple so he sees the earth moving with a relative velocity vea.
Any other observer on earth will see the apple moving towards earth with velocity vae.
Both are opposite in direction.
Q.8. Suppose the gravitational potential due to a small system is k/r2 at a distance r from it. What will be the gravitational field? Can you think of any such system? What happens if there were negative masses?
The gravitational potential due to the system is given as V = k/r2
Gravitational field due to the system :
We can see that for this system, E ∝ (1/r3)
This type of system is not possible because Fg is always proportional to inverse of square of distance(experimental fact).
If there were negative masses, then this type of system is possible.
This system is a dipole of two masses, i.e., two masses, one positive and the other negative, separated by a small distance.
In this case, the gradational field due to the dipole is proportional to 1/r3.
Q.9. The gravitational potential energy of a two-particle system is derived in this chapter as 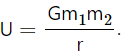 Does it follow from this equation that the potential energy for r = ∞ must be zero? Can we choose the potential energy for r = ∞ to be 20 J and still use this formula? If no, what formula should be used to calculate the gravitational potential energy at separation r ?
Does it follow from this equation that the potential energy for r = ∞ must be zero? Can we choose the potential energy for r = ∞ to be 20 J and still use this formula? If no, what formula should be used to calculate the gravitational potential energy at separation r ?
The gravitational potential energy of a two-particle system is given by
This relation does not tell that the gravitational potential energy is zero at infinity. For our convenience, we choose the potential energies of the two particles to be zero when the separation between them is infinity. No, if we suppose that the potential energy for r = ∞ is 20 J, then we need to modify the formula. Now, potential energy of the two-particle system separated by a distance r is given by
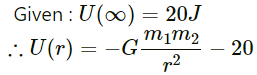
This formula should be used to calculate the gravitational potential energy at separation r.
Q.10. The weight of an object is more at the poles than at the equator. Is it beneficial to purchase goods at equator and sell them at the pole? Does it matter whether a spring balance is used or an equal-beam balance is used?
The weight of an object is more at the poles than that at the equator. In purchasing or selling goods, we measure the mass of the goods. The balance used to measure the mass is calibrated according to the place to give its correct reading. So, it is not beneficial to purchase goods at the equator and sell them at the poles. A beam balance measures the mass of an object, so it can be used here. For using a spring balance, we need to calibrate it according to the place to give the correct readings.
Q.11. The weight of a body at the poles is greater than the weight at the equator. Is it the actual weight or the apparent weight we are talking about? Does your answer depend on whether only the earth's rotation is taken into account or the flattening of the earth at the poles is also taken into account?
The weight of a body at the poles is greater than that at the equator. Here, we are talking about the actual weight of the body at that particular place.
Yes. If the rotation of the Earth is taken into account, then we are discussing the apparent weight of the body.
Q.12. If the radius of the earth decreases by 1% without changing its mass, will the acceleration due to gravity at the surface of the earth increase or decrease? If so, by what per cent?
If we consider the Earth to be a perfect sphere, then the acceleration due to gravity at its surface is given by
Here, M is the mass of Earth; R is the radius of the Earth and G is universal gravitational constant.
If the radius of the earth is decreased by 1%, then the new radius becomes
New acceleration due to gravity will be given by
Hence, the value of the acceleration due to gravity increases when the radius is decreased. Percentage increase in the acceleration due to gravity is given by
= 2 %
Q.13. A nut becomes loose and gets detached from a satellite revolving around the earth. Will it land on the earth? If yes, where will it land? If no, how can an astronaut make it land on the earth?
No, it will not land on the Earth. The nut will start revolving in the orbit of the satellite with the same orbital speed as that of the satellite due to inertia of motion. An astronaut can make it land on the Earth by projecting it with some velocity toward the Earth.
Q.14. Is it necessary for the plane of the orbit of a satellite to pass through the centre of the earth?
According to Kepler first law of planetary motion all planets move in elliptical orbits with sun at one of its foci. It applies to any planet and its satellite as well. This implies that plane of the satellite has to pass through the centre of planet (earth).
Q.15. Consider earth satellites in circular orbits. A geostationary satellite must be at a height of about 36000 km from the earth's surface. Will any satellite moving at this height be a geostationary satellite? Will any satellite moving at this height have a time period of 24 hours?
= 24.097 Hr
Which implies that it is a geostationary sattelite with time period = 24 Hrs.
Q.16. No part of India is situated on the equator. Is it possible to have a geostationary satellite which always remains over New Delhi?
No. All geostationary orbits are concentric with the equator of the Earth.
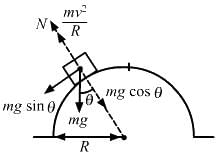
Q.17. As the earth rotates about its axis, a person living in his house at the equator goes in a circular orbit of radius equal to the radius of the earth. Why does he/she not feel weightless as a satellite passenger does?
A person living in a house at the equator will not feel weightlessness because he is not in a free fall motion. Satellites are in free fall motion under the gravitational pull of the earth, but, due to the curved surface of the Earth, they move in a circular path. The gravitational force on the satellite due to the Sun provides the centripetal force for its revolution. Therefore, net force on the satellite is zero and, thus, a person feels weightless in a satellite orbiting the earth.
Q.18. Two satellites going in equatorial plane have almost same radii. As seen from the earth one moves from east one to west and the other from west to east. Will they have the same time period as seen from the earth? If not which one will have less time period?
No, both satellites will have different time periods as seen from the Earth. The satellite moving opposite (east to west) to the rotational direction of the Earth will have less time period, because its relative speed with respect to the Earth is more.
Q.19. A spacecraft consumes more fuel in going from the earth to the moon than it takes for a return trip. Comment on this statement.
Yes, a spacecraft consumes more fuel in going from the Earth to the Moon than it takes for the return trip. In going from the Earth to the Moon, the spacecraft has to overcome the gravitational pull of the earth. So, more fuel is consumed in going from the Earth to Moon. However, in the return trip, this gravitation pull helps the spacecraft to come back to the Earth.
Multiple Choice Questions
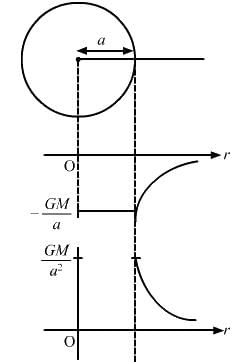
(A) The plot of V against r is discontinuous.
(B) The plot of E against r is discontinuous.
(A) the plot of V against r is discontinuous.
(B) The plot of E against r is discontinuous.
(A) There are points outside the earth where the value of g is equal to its value at the equator.
(B) There are points outside the earth where the value of g is equal to its value at the poles.
|
134 docs
|
FAQs on HC Verma Questions and Solutions: Chapter 11: Gravitation- 1 - HC Verma Solutions - JEE
| 1. What is the formula for gravitational force? |  |
| 2. How does the gravitational force vary with distance? |  |
| 3. What is the difference between mass and weight? |  |
| 4. How does the gravitational force affect the motion of objects? |  |
| 5. How does the gravitational force affect the orbits of planets? |  |