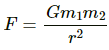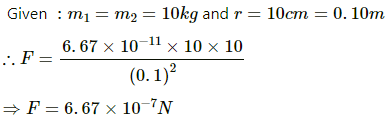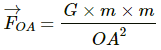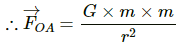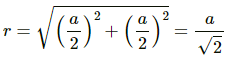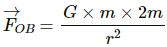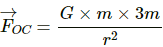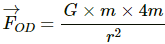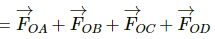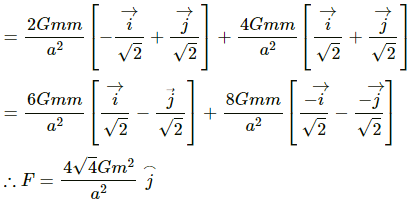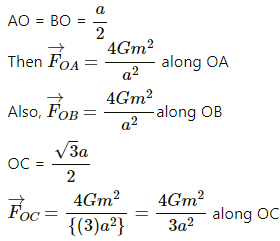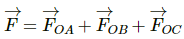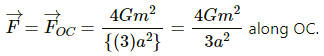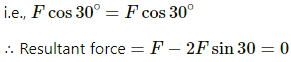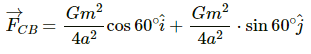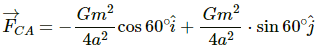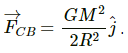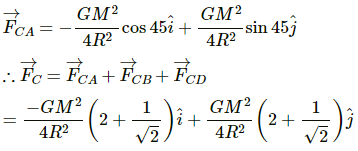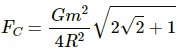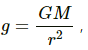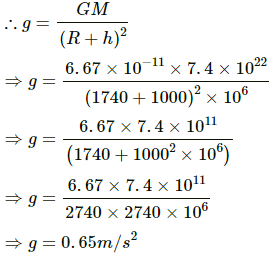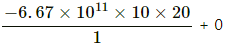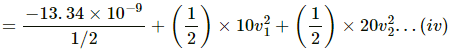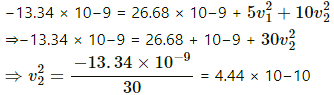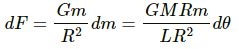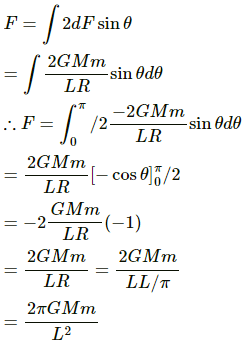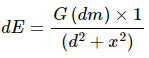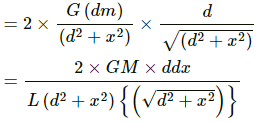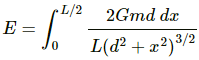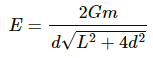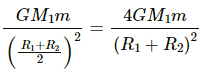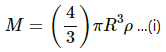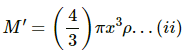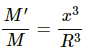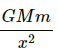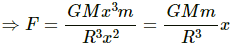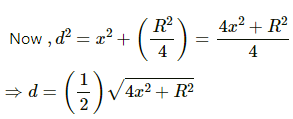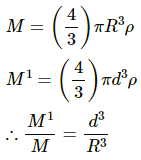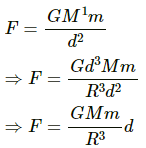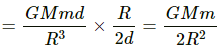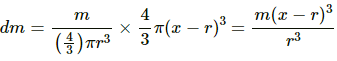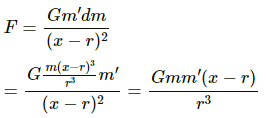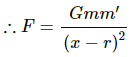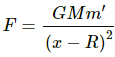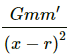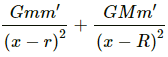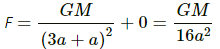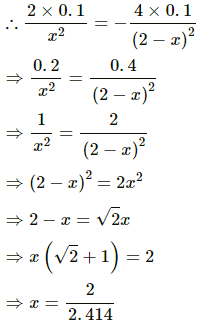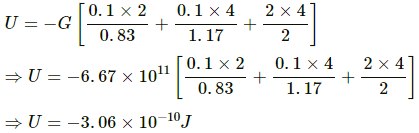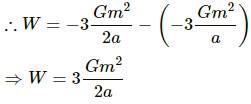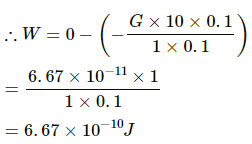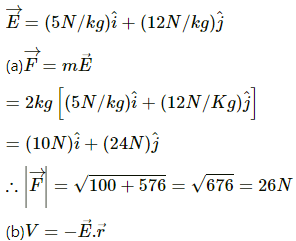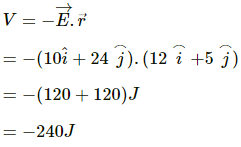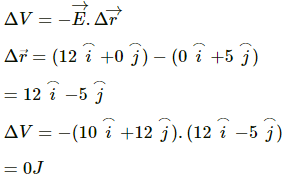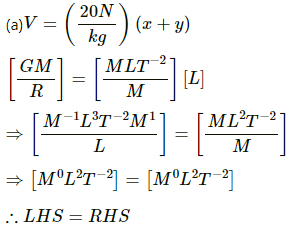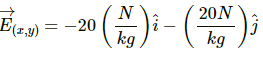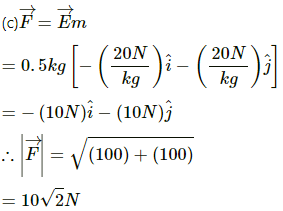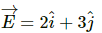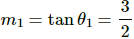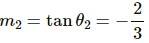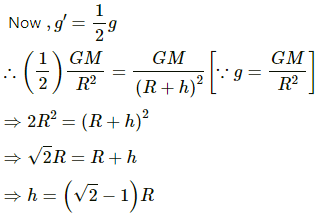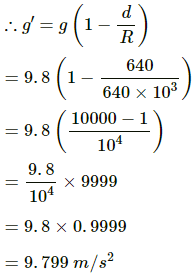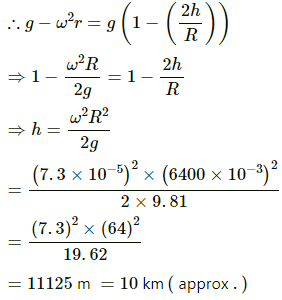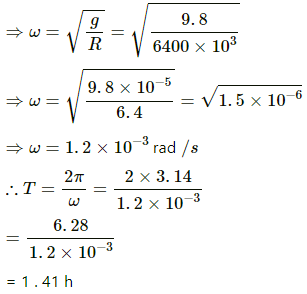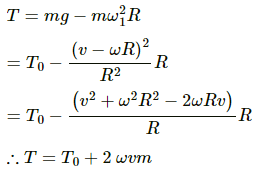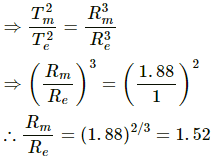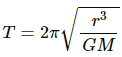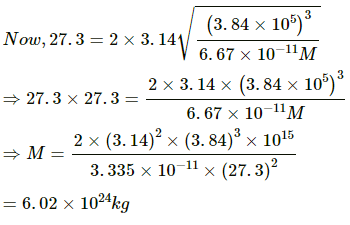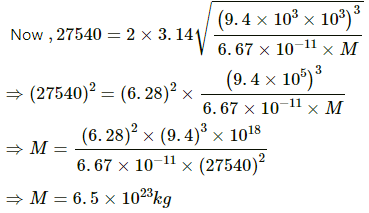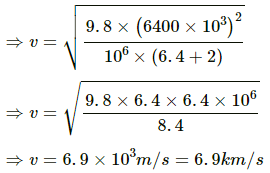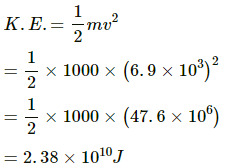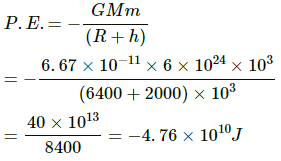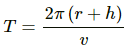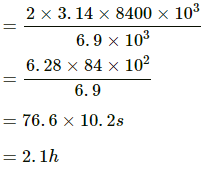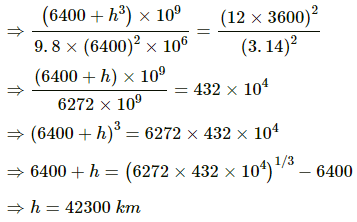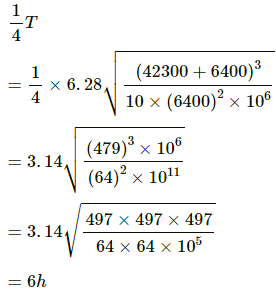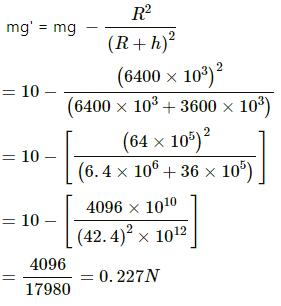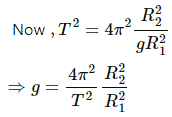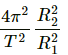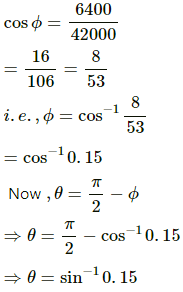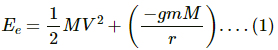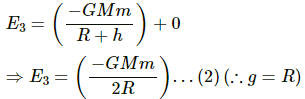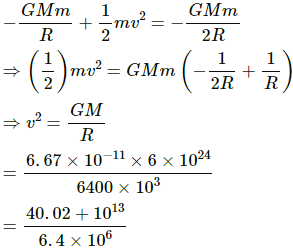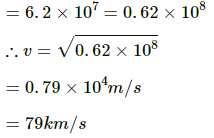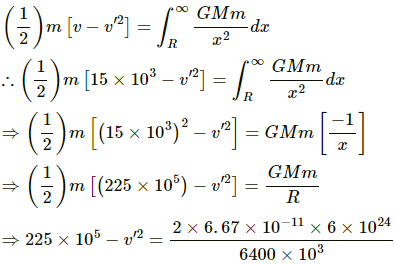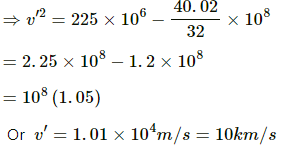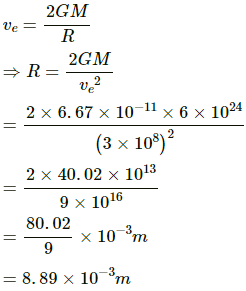HC Verma Questions and Solutions: Chapter 11: Gravitation- 2 | HC Verma Solutions - JEE PDF Download
Exercise
Q.1. Two spherical balls of mass 10 kg each are placed 10 cm apart. Find the gravitational force of attraction between them.
The gravitational force of attraction between the balls is given as by
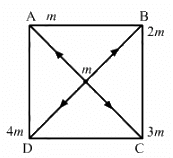
Q.2. Four particles having masses m, 2m, 3m and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the centre.
Force due to the particle at A,
Let OA = r
Here,
Force due to the particle at B,
Force due to the particle at C,
Force due to the particle at D,
Now, resultant force
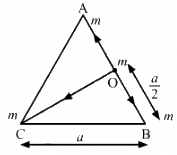
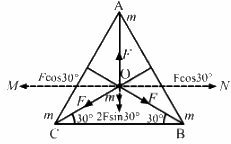
Q.3. Three equal masses m are placed at the three corners of an equilateral triangle of side a. Find the force exerted by this system on another particle of mass m placed at (a) the mid-point of a side, (b) at the centre of the triangle.
(a) Consider that mass 'm' is placed at the midpoint O of side AB of equilateral triangle ABC.
The net force on the particle at O is
Since equal and opposite forces cancel each other, we have :
(b) If the particle placed at O (centroid)
All the forces are equal in magnitude but their directions are different as shown in the figure.
Equal and opposite forces along OM and ON cancel each other.
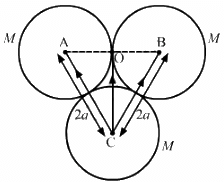
Q.4. Three uniform spheres each having a mass M and radius a are kept in such a way that each touches the other two. Find the magnitude of the gravitational force on any of the spheres due to the other two.
Three spheres are placed with their centres at A, B and C as shown in the figure.
Gravitational force on sphere C due to sphere B is given by
Gravitational force on sphere C due to sphere A is given by
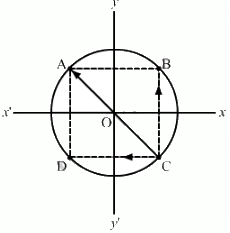
Q.5. Four particles of equal masses M move along a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
Assume that three particles are at points A, B and C on the circumference of a circle.
BC = CD = √2a
The force on the particle at C due to gravitational attraction of the particle at B is
The force on the particle at C due to gravitational attraction of the particle at D is
Now, force on the particle at C due to gravitational attraction of the particle at A is given by
So, the resultant gravitational force on C is
Let v be the velocity with which the particle is moving.
Centripetal force on the particle is given by
Q.6. Find the acceleration due to gravity of the moon at a point 1000 km above the moon's surface. The mass of the moon is 7.4 × 1022 kg and its radius is 1740 km.
The acceleration due to gravity at a point at height h from the surface of the moon is given by
where M is the mass of the moon; r is the distance of point from the centre of the moon and G is universal gravitational constant.
Q.7. Two small bodies of masses 10 kg and 20 kg are kept a distance 1.0 m apart and released. Assuming that only mutual gravitational forces are acting, find the speeds of the particles when the separation decreases to 0.5 m.
Consider a system of two bodies. The initial linear momentum of the system is zero as the bodies were initially at rest when they were released.
Since the gravitational force is an internal force and the net external force on the system is zero, so by the law of conservation of linear momentum, the final momentum of the system will also be zero.
So, 10 x v1 = 20 x v2
⇒ v1 = 2 v2 ...(i)
Applying the law of conservation of energy,We have;
Initial total energy = final total energy ...(ii)
Initial total energy =
= −13.34 × 10−9 J ...(iii)
When the separation is 0.5 m, we have:
Final total energy=
From (iii) and (iv), we have:
⇒ v2 = 2.1 × 10−5 m/s
∴ v1 = 4.2 × 10−5 m/s
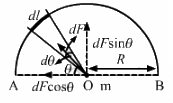
Q.8. A semicircular wire has a length L and mass M. A particle of mass m is placed at the centre of the circle. Find the gravitational attraction on the particle due to the wire.
Consider a small mass element of length dl subtending dθ angle at the centre.
In the semicircle, we can consider a small element dθ.
Then length of the element, dl = R dθ
Mass of the element, dm = (M/L)Rdθ
Force on the mass element is given by
The symmetric components along AB cancel each other.
Now, net gravitational force on the particle at O is given by
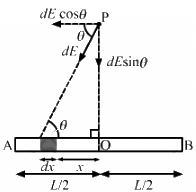
Q.9. Derive an expression for the gravitational field due to a uniform rod of length L and mass M at a point on its perpendicular bisector at a distance d from the centre.
Consider a small mass element of length dx at a distance x from the centre of the rod.
Mass of the mass element, dm = (M/L) × dx
Gravitational field due to this element at point P is given by
The components of the gravitational field due to the symmetrical mass element along the length of the rod cancel each other.
Now, resultant gravitational field = 2dE sin θ
Total gravitational field due to the rod at point P is given by
On integrating the above equation, we get :
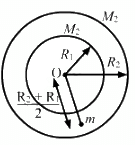
Q.10. Two concentric spherical shells have masses M1, M2 and radii R1, R2 (R1 < R2). What is the force exerted by this system on a particle of mass m1 if it is placed at a distance (R1+ R2)/2 from the centre?
Consider that mass m is at a distance
as shown in the figure.
The gravitational force of m due to the shell of M2 is zero, because the mass is inside the shell.
∴ Gravitational force due to the shell of mass M2 =
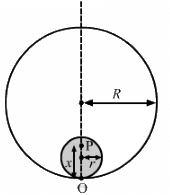
Q.11. A tunnel is dug along a diameter of the earth. Find the force on a particle of mass m placed in the tunnel at a distance x from the centre.
Mass of the Earth,
Consider an imaginary sphere of radius x with centre O as shown in the figure below :
Mass of the imaginary sphere,
From (i) and (ii), we have :
∴ Gravitational force on the particle of mass m is given by F =
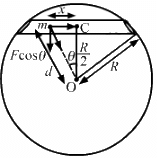
Q.12. A tunnel is dug along a chord of the earth at a perpendicular distance R/2 from the earth's centre. The wall of the tunnel may be assumed to be frictionless. Find the force exerted by the wall on a particle of mass m when it is at a distance x from the centre of the tunnel.
Let d be distance of the particle from the centre of the Earth.
Let M be the mass of the Earth and M' be the mass of the sphere of radius d.
Then we have :
Gravitational force on the particle of mass m is given by
∴ Normal force exerted by the wall, FN = F cos θ
Q.13. A solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in the following figure . A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if (a) r < x < 2r, (b) 2r < x < 2R and (c) x > 2R.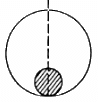
(a) Consider that the particle is placed at a distance x from O.
Here, r < x < 2r
Let us consider a thin solid sphere of radius (x − r).
Mass of the sphere,
Then the gravitational force on the particle due to the solid sphere is given by
Force on the particle due to the shell will be zero because gravitational field intensity inside a shell is zero.
(b) If 2r < x < 2R,
Force on the body due to the shell will again be zero as particle is still inside the shell.
then F is only due to the solid sphere.
(c) If x > 2R, then the gravitational force is due to both the sphere and the shell.
Now, we have :
Gravitational force due to shell,
Gravitational force due to the sphere =
As both the forces are acting along the same line joining the particle with the centre of the sphere and shell so both the forces can be added directly without worrying about their vector nature.
∴ Resultant force =
Q.14. A uniform metal sphere of radius a and mass M is surrounded by a thin uniform spherical shell of equal mass and radius 4a (In the following figure). The centre of the shell falls on the surface of the inner sphere. Find the gravitational field at the points P1 and P2 shown in the figure.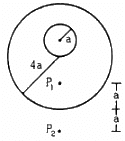
At point P1, the gravitational field due to the sphere and the shell is given by
At point P2, the gravitational field due to the sphere and the shell is given by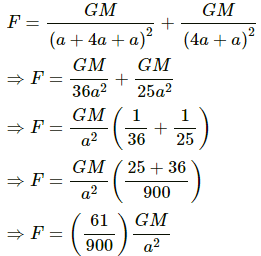
Q.15. A thin spherical shell having uniform density is cut in two parts by a plane and kept separated as shown in the following figure. The point A is the centre of the plane section of the first part and B is the centre of the plane section of the second part. Show that the gravitational field at A due to the first part is equal in magnitude to the gravitational field at B due to the second part.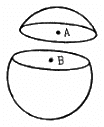
We know that in a thin spherical shell of uniform density, the gravitational field at its internal point is zero. So, at points A and B, the gravitational fields are equal and opposite and, thus, cancel each other. So the net field is zero.
Hence, EA = EB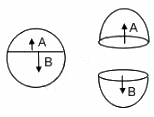
Q.16. Two small bodies of masses 2.00 kg and 4.00 kg are kept at rest at a separation of 2.0 m. Where should a particle of mass 0.10 kg be placed to experience no net gravitational force from these bodies? The particle is placed at this point. What is the gravitational potential energy of the system of three particles with usual reference level?
Let the mass of 0.10 kg be at a distance x from the 2 kg mass and at a distance of (2 − x) from the 4 kg mass.
Force between 0.1 kg mass and 2 kg mass = force between 0.1 kg mass and 4 kg mass
= 0.83 m from the 2 kg mass
Now, gravitation potential energy of the system is given by
Q.17. Three particles of mass m each are placed at the three corners of an equilateral triangle of side a. Find the work which should be done on this system to increase the sides of the triangle to 2a.
The work done in increasing the side of the triangle from a to 2a is equal to the difference of the potential energies of the system.
i.e., work done = final potential energy of the system − initial potential energy of the system
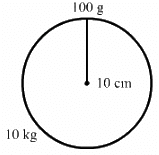
Q.18. A particle of mass 100 g is kept on the surface of a uniform sphere of mass 10 kg and radius 10 cm. Find the work to be done against the gravitational force between them to take the particle away from the sphere.
The work done against the gravitational force to take the particle away from the sphere to infinity is equal to the difference between the potential energy of the particle at infinity and potential energy of the particle at the surface of the sphere.
Q.19. The gravitational field in a region is given by 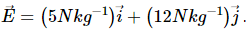 (a) Find the magnitude of the gravitational force acting on a particle of mass 2 kg placed at the origin. (b) Find the potential at the points (12 m, 0) and (0, 5 m) if the potential at the origin is taken to be zero. (c) Find the change in gravitational potential energy if a particle of mass 2 kg is taken from the origin to the point (12 m, 5 m). (d) Find the change in potential energy if the particle is taken from (12 m, 0) to (0, 5 m).
(a) Find the magnitude of the gravitational force acting on a particle of mass 2 kg placed at the origin. (b) Find the potential at the points (12 m, 0) and (0, 5 m) if the potential at the origin is taken to be zero. (c) Find the change in gravitational potential energy if a particle of mass 2 kg is taken from the origin to the point (12 m, 5 m). (d) Find the change in potential energy if the particle is taken from (12 m, 0) to (0, 5 m).
Gravitational field,
Potential at (12 m, 0) = -60J/Kg
Potential at (0, 5 m) = -60J/Kg
(c)
change in potential = final potential -initial potential
initial potential = potential at the origin = 0
final potential = potential at (12,5)
(d)
Q.20. The gravitational potential in a region is given by V = 20 N kg−1 (x + y). (a) Show that the equation is dimensionally correct. (b) Find the gravitational field at the point (x, y). Leave your answer in terms of the unit vectors 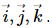 (c) Calculate the magnitude of the gravitational force on a particle of mass 500 g placed at the origin.
(c) Calculate the magnitude of the gravitational force on a particle of mass 500 g placed at the origin.
(b) The gravitational field at the point (x, y) is given by
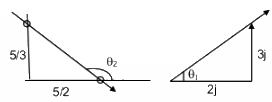
Q.21. The gravitational field in a region is given by 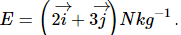 Show that no work is done by the gravitational field when a particle is moved on the line 3y + 2x = 5.
Show that no work is done by the gravitational field when a particle is moved on the line 3y + 2x = 5.
[Hint : If a line y = mx + c makes angle θ with the X-axis, m = tan θ.]
The gravitational field in a region is given by
Slope of the electric field,
The given line is 3y + 2x = 5.
Slope of the line,
We can see that m1m2 = −1
Since the directions of the field and the displacement are perpendicular to earth other, no work is done by the gravitational field when a particle is moved on the given line.
Q.22. Find the height over the Earth's surface at which the weight of a body becomes half of its value at the surface.
Assume that at height h, the weight of the body becomes half.
Weight of the body at the surface = mg
Weight of the body at height h above the Earth's surface = mg', where g' is the acceleration due to gravity at height h
Q.23. What is the acceleration due to gravity on the top of Mount Everest? Mount Everest is the highest mountain peak of the world at the height of 8848 m. The value at sea level is 9.80 m s−2.
Let g' be the acceleration due to gravity on Mount Everest.
Then
∴ The acceleration due to gravity on the top of Mount Everest is 9.77 m/s2.
Q.24. Find the acceleration due to gravity in a mine of depth 640 m if the value at the surface is 9.800 m s−2. The radius of the earth is 6400 km.
Let g' be the acceleration due to gravity in a mine of depth d.
Q.25. A body is weighed by a spring balance to be 1.000 kg at the North Pole. How much will it weigh at the equator? Account for the earth's rotation only.
Let gp be the acceleration due to gravity at the poles.
Let ge be the acceleration due to gravity at the equator.
Now, acceleration due to gravity at the equator is given by ge = gp - ω2r
= 9.81 − (7.3 × 10−5)2 × 6400 × 103
= 9.81 − (53.29 × 10−10) × 64 × 105
= 9.81 − 0.034 = 9.776 m/s2
Now, mge = 1 kg × 9.776 m/s2
= 9.776 N
∴ The body will weigh 9.776 N at the equator.
Q.26. A body stretches a spring by a particular length at the earth's surface at the equator. At what height above the south pole will it stretch the same spring by the same length? Assume the earth to be spherical.
At the equator, g' = g − ω2R ...(i)
Let h be the height above the South Pole where the body stretch the spring by the same length.
The acceleration due to gravity at this point is
Weight of the body at the equator = weight of the body at height h above the South Pole
Q.27. At what rate should the earth rotate so that the apparent g at the equator becomes zero? What will be the length of the day in this situation?
The apparent acceleration due to gravity at the equator becomes zero.
i.e., g' = g − ω2R = 0
⇒ g = ω2R
Q.28. A pendulum having a bob of mass m is hanging in a ship sailing along the equator from east to west. When the ship is stationary with respect to water the tension in the string is T0. (a) Find the speed of the ship due to rotation of the earth about its axis. (b) Find the difference between T0 and the earth's attraction on the bob. (c) If the ship sails at speed v, what is the tension in the string? Angular speed of earth's rotation is ω and radius of the earth is R.
(a) Speed of the ship due to rotation of the Earth is v = ωR, where R is the radius of the Earth and ω is its angular speed.
(b) The tension in the string is given by
T0 = mg − mω2R
∴ T0 − mg = mω2R
(c) Let the ship move with a speed v.
Then the tension in the string is given by
Q.29. The time taken by Mars to revolve round the Sun is 1.88 years. Find the ratio of average distance between Mars and the sun to that between the earth and the sun.
According to Kepler's laws of planetary motion, the time period of revolution of a planet about the Sun is directly proportional to the cube of the distance between their centres.
i.e., T2 ∝ R3
Q.30. The moon takes about 27.3 days to revolve round the earth in a nearly circular orbit of radius 3.84 × 105 km/ Calculate the mass of the earth from these data.
Time period of rotation of the Moon around the Earth is given by
where r is the distance between the centres of the Earth and Moon and m is the mass of the Earth.
∴ The mass of the Earth is found to be 6.02× 1024 kg.
Q.31. A Mars satellite moving in an orbit of radius 9.4 × 103 km takes 27540 s to complete one revolution. Calculate the mass of Mars.
Time period of revolution of the satellite around the Mars is give by
where M is the mass of the Mars and r is the distance of the satellite from the centre of the planet.
Q.32. A satellite of mass 1000 kg is supposed to orbit the earth at a height of 2000 km above the earth's surface. Find (a) its speed in the orbit, (b) is kinetic energy, (c) the potential energy of the earth-satellite system and (d) its time period. Mass of the earth = 6 × 1024kg.
(a) Speed of the satellite in its orbit
(b) Kinetic energy of the satellite
(c) Potential energy of the satellite
(d) Time period of the satellite
Q.33. (a) Find the radius of the circular orbit of a satellite moving with an angular speed equal to the angular speed of earth's rotation. (b) If the satellite is directly above the North Pole at some instant, find the time it takes to come over the equatorial plane. Mass of the earth = 6 × 1024 kg.
(a) The angular speed of the Earth and the satellite will be the same.
(b) Time taken from the North Pole to the equatorial plane is given by
Q.34. What is the true weight of an object in a geostationary satellite that weighed exactly 10.0 N at the north pole?
For a geostationary satellite, we have:
R = 6.4 × 103 km
h = 3.6 × 103 km
Given: mg = 10 N
The true weight of the object in the geostationary satellite is given by
Q.35. The radius of a planet is R1 and a satellite revolves round it in a circle of radius R2. The time period of revolution is T. Find the acceleration due to the gravitation of the planet at its surface.
The time period of revolution of the satellite around a planet in terms of the radius of the planet and radius of the orbit of the satellite is given by
where g is the acceleration due to gravity at the surface of the planet.
∴ Acceleration due to gravity of the planet =
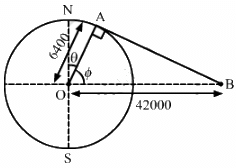
Q.36. Find the minimum colatitude which can directly receive a signal from a geostationary satellite.
Consider that B is the position of the geostationary satellite.
In the given figure, ∅ is the latitude and θ is the colatitude of a place which can directly receive a signal from a geostationary satellite.
In triangle OAB, we have:
Q.37. A particle is fired vertically upward from earth's surface and it goes up to a maximum height of 6400 km. Find the initial speed of particle.
The particle attained a maximum height 6400 km, which is equal to the radius of the Earth.
Total energy of the particle on the Earth's surface is given by
Now, total energy of the particle at the maximum height is given by
From equations (1) and (2), we have:
Q.38. A particle is fired vertically upward with a speed of 15 km s−1. With what speed will it move in interstellar space. Assume only earth's gravitational field.
Initial velocity of the particle, v = 15 km/s
Let its speed be v' in interstellar space.
Applying the law of conservation of energy, we have:
Q.39. A mass of 6 × 1024 kg (equal to the mass of the earth) is to be compressed in a sphere in such a way that the escape velocity from its surface is 3 × 108 ms−1. What should be the radius of the sphere?
Mass of the sphere = 6 × 1024 kg
Escape velocity = 3 × 108 m/s
Escape velocity is given by
= 9 mm
|
134 docs
|
FAQs on HC Verma Questions and Solutions: Chapter 11: Gravitation- 2 - HC Verma Solutions - JEE
| 1. How does the force of gravity affect objects on Earth? |  |
| 2. Can the force of gravity change with distance? |  |
| 3. What is the difference between mass and weight? |  |
| 4. What is the value of acceleration due to gravity on Earth? |  |
| 5. How does the force of gravity vary on different planets? |  |