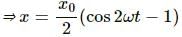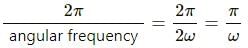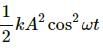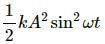Short Answers
Q.1. A person goes to bed at sharp 10.00 pm every day. Is it an example of periodic motion? If yes, what is the time period? If no, why?
No. As motion is a change in position of an object with respect to time or a reference point, it is not an example of periodic motion.
Q.2. A particle executing simple harmonic motion comes to rest at the extreme positions. Is the resultant force on the particle zero at these positions according to Newton's first law?
No. The resultant force on the particle is maximum at the extreme positions.
Q.3. Can simple harmonic motion take place in a non-inertial frame? If yes, should the ratio of the force applied with the displacement be constant?
Yes. Simple harmonic motion can take place in a non-inertial frame. However, the ratio of the force applied to the displacement cannot be constant because a non-inertial frame has some acceleration with respect to the inertial frame. Therefore, a fictitious force should be added to explain the motion.
Q.4. A particle executes simple harmonic motion. If you are told that its velocity at this instant is zero, can you say what is its displacement? If you are told that its velocity at this instant is maximum, can you say what is its displacement?
No, we cannot say anything from the given information. To determine the displacement of the particle using its velocity at any instant, its mean position has to be known.
Q.5. A small creature moves with constant speed in a vertical circle on a bright day. Does its shadow formed by the sun on a horizontal plane move in a sample harmonic motion?
Yes, its shadow on a horizontal plane moves in simple harmonic motion. The projection of a uniform circular motion executes simple harmonic motion along its diameter (which is the shadow on the horizontal plane), with the mean position lying at the centre of the circle.
Q.6. A particle executes simple harmonic motion Let P be a point near the mean position and Q be a point near an extreme. The speed of the particle at P is larger than the speed at Q. Still the particle crosses P and Q equal number of times in a given time interval. Does it make you unhappy?
No. It does not make me unhappy because the number of times a particle crosses the mean and extreme positions does not depend on the speed of the particle.
Q.7. In measuring time period of a pendulum, it is advised to measure the time between consecutive passage through the mean position in the same direction. This is said to result in better accuracy than measuring time between consecutive passage through an extreme position. Explain.
The mean position of a particle executing simple harmonic motion is fixed, whereas its extreme position keeps on changing. Therefore, when we use stop watch to measure the time between consecutive passage, we are certain about the mean position.
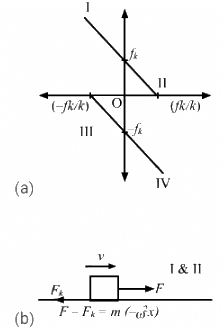
Q.8. It is proposed to move a particle in simple harmonic motion on a rough horizontal surface by applying an external force along the line of motion. Sketch the graph of the applied force against the position of the particle. Note that the applied force has two values for a given position depending on whether the particle is moving in positive or negative direction.
Figure (a) shows the graph of the applied force against the position of the particle.
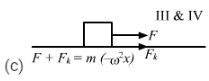
Q.9. Can the potential energy in a simple harmonic motion be negative? Will it be so if we choose zero potential energy at some point other than the mean position?
No. It cannot be negative because the minimum potential energy of a particle executing simple harmonic motion at mean position is zero. The potential energy increases in positive direction at the extreme position.
However, if we choose zero potential energy at some other point, say extreme position, the potential energy can be negative at the mean position.
Q.10. The energy of system in simple harmonic motion is given by 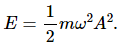 Which of the following two statements is more appropriate?
Which of the following two statements is more appropriate?
(A) The energy is increased because the amplitude is increased.
(B) The amplitude is increased because the energy is increased.
Statement A is more appropriate because the energy of a system in simple harmonic motion is given by 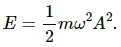
If the mass (m) and angular frequency (ω) are made constant, Energy (E) becomes proportional to the square of amplitude (A2).
i.e. E ∝ A2
Therefore, according to the relation, energy increases as the amplitude increases.
Q.11. A pendulum clock gives correct time at the equator. Will it gain time or loose time as it is taken to the poles?
According to the relation :  The time period (T) of the pendulum becomes proportional to the square root of inverse of g if the length of the pendulum is kept constant.
The time period (T) of the pendulum becomes proportional to the square root of inverse of g if the length of the pendulum is kept constant.
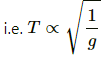
Also, acceleration due to gravity (g) at the poles is more than that at equator. Therefore, the time period decreases and the clock gains time.
Q.12. Can a pendulum clock be used in an earth-satellite?
No. According to the relation :
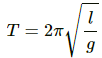
The time period of the pendulum clock depends upon the acceleration due to gravity. As the earth-satellite is a free falling body and its geffective (effective acceleration due to gravity ) is zero at the satellite, the time period of the clock is infinite.
Q.13. A hollow sphere filled with water is used as the bob of a pendulum. Assume that the equation for simple pendulum is valid with the distance between the point of suspension and centre of mass of the bob acting as the effective length of the pendulum. If water slowly leaks out of the bob, how will the time period vary?
The time period of a pendulum depends on the length and is given by the relation, 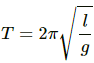
As the effective length of the pendulum first increases and then decreases, the time period first increases and then decreases.
Q.14. A block of known mass is suspended from a fixed support through a light spring. Can you find the time period of vertical oscillation only by measuring the extension of the spring when the block is in equilibrium?
Yes.
Time period of a spring mass system is given by, 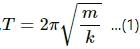 where m is mass of the block, and k is the spring constant Time period is also given by the relation,
where m is mass of the block, and k is the spring constant Time period is also given by the relation, 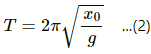
where, x0 is extension of the spring, and g is acceleration due to gravity
From the equations (1) and (2), we have :
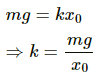
Substituting the value of k in the above equation, we get:
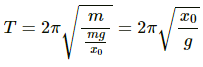
Thus, we can find the time period if the value of extension x0 is known.
Q.15. A platoon of soldiers marches on a road in steps according to the sound of a marching band. The band is stopped and the soldiers are ordered to break the steps while crossing a bridge. Why?
When the frequency of soldiers' feet movement becomes equal to the natural frequency of the bridge, and resonance occurs between soldiers' feet movement and movement of the bridge, maximum transfer of energy occurs from soldiers' feet to the bridge, which increases the amplitude of vibration. A continued increase in the amplitude of vibration, however, may lead to collapsing of the bridge.
Q.16. The force acting on a particle moving along X-axis is F = −k(x − vo t) where k is a positive constant. An observer moving at a constant velocity v0 along the X-axis looks at the particle. What kind of motion does he find for the particle?
As the observer moves with a constant velocity along the same axis, he sees the same force on the particle and finds the motion of the particle is not simple harmonic motion.
Multiple Choice Questions
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:A student says that he had applied a force F = -k√x on a particle and the particle moved in simple harmonic motion. He refuses to tell whether k is a constant or not. Assume that he was worked only with positive x and no other force acted on the particle.
Explanation
A body is said to be in simple harmonic motion only when,
F = −kx ...(1)
where F is force,
k is force constant, and x is displacement of the body from the mean position.
Given:
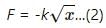
On comparing the equations (1) and (2), it can be said that in order to execute simple harmonic motion, k should be proportional to 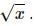
Thus, as x increases k increases.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:The time period of a particle in simple harmonic motion is equal to the time between consecutive appearances of the particle at a particular point in its motion. This point is
Explanation
One oscillation is said to be completed when the particle returns to the extreme position i.e. from where it started.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:The time period of a particle in simple harmonic motion is equal to the smallest time between the particle acquiring a particular velocity 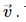 The value of v is
The value of v is
Explanation
Because the time period of a simple harmonic motion is defined as the time taken to complete one oscillation.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:The displacement of a particle in simple harmonic motion in one time period is
Explanation
Displacement is defined as the distance between the starting and the end point through a straight line. In one complete oscillation, the net displacement is zero as the particle returns to its initial position.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:The distance moved by a particle in simple harmonic motion in one time period is
Explanation
In an oscillation, the particle goes from one extreme position to other extreme position that lies on the other side of mean position and then returns back to the initial extreme position. Thus, total distance moved by particle is, 2A + 2A = 4A.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:The average acceleration in one time period in a simple harmonic motion is
Explanation
The acceleration changes its direction (to opposite direction) after every half oscillation. Thus, net acceleration is given as, Aω2 + ( -Aω2) = 0
Report a problem
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:The motion of a particle is given by x = A sin ωt + B cos ωt. The motion of the particle is
Explanation
Report a problem
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:The displacement of a particle is given by 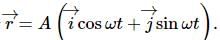 The motion of the particle is
The motion of the particle is
Explanation
We know,
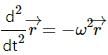
But there is a phase difference of 90o between the x and y components because of which the particle executes a circular motion and hence, the projection of the particle on the diameter executes a simple harmonic motion.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:A particle moves on the X-axis according to the equation x = A + B sin ωt. The motion is simple harmonic with amplitude
Explanation
At t = 0,
Displacement (x0) is given by, x0 = A + sin ω(0) = A
Displacement x will be maximum when sinωt is 1 or, xm = A + B
Amplitude will be: xm − xo = A + B − A = B
Report a problem
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:Figure represents two simple harmonic motions.
The parameter which has different values in the two motions is 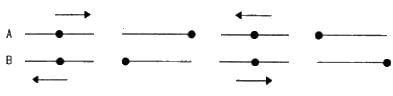
Explanation
Because the direction of motion of particles A and B is just opposite to each other.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:The total mechanical energy of a spring-mass system in simple harmonic motion is 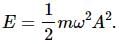 Suppose the oscillating particle is replaced by another particle of double the mass while the amplitude A remains the same. The new mechanical energy will
Suppose the oscillating particle is replaced by another particle of double the mass while the amplitude A remains the same. The new mechanical energy will
Explanation
Report a problem
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:The average energy in one time period in simple harmonic motion is
Explanation
It is the total energy in simple harmonic motion in one time period.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:A particle executes simple harmonic motion with a frequency v. The frequency with which the kinetic energy oscillates is
Explanation
Because in one complete oscillation, the kinetic energy changes its value from zero to maximum, twice.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:A particle executes simple harmonic motion under the restoring force provided by a spring. The time period is T. If the spring is divided in two equal parts and one part is used to continue the simple harmonic motion, the time period will
Explanation
Time period (T) is given by,
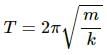
where m is the mass, and k is spring constant.
When the spring is divided into two parts, the new spring constant k1 is given as, k1 = 2k
New time period T1 :
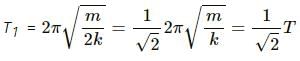
Report a problem
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:Two bodies A and B of equal mass are suspended from two separate massless springs of spring constant k1 and k2 respectively. If the bodies oscillate vertically such that their maximum velocities are equal, the ratio of the amplitude of A to that of B is
Explanation
Maximum velocity, v = Aω
where A is amplitude and ω is the angular frequency.
Further, ω = 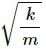
Let A and B be the amplitudes of particles A and B respectively. As the maximum velocity of particles are equal,
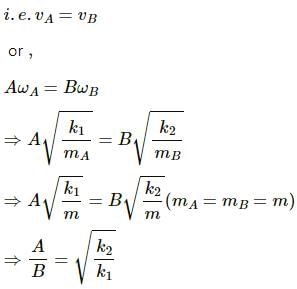
Report a problem
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:A spring-mass system oscillates with a frequency v. If it is taken in an elevator slowly accelerating upward, the frequency will
Explanation
Because the frequency 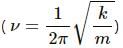 of the system is independent of the acceleration of the system.
of the system is independent of the acceleration of the system.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:A spring-mass system oscillates with a car. If the car accelerates on a horizontal road, the frequency of oscillation will
Explanation
As the frequency of the system is independent of the acceleration of the system.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:A pendulum clock that keeps correct time on the earth is taken to the moon. It will run
Explanation
The acceleration due to gravity at moon is g/6.
Time period of pendulum is given by,
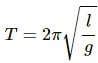
Therefore, on moon, time period will be :
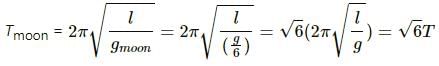
Report a problem
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:A wall clock uses a vertical spring-mass system to measure the time. Each time the mass reaches an extreme position, the clock advances by a second. The clock gives correct time at the equator. If the clock is taken to the poles it will
Explanation
Because the time period of a spring-mass system does not depend on the acceleration due to gravity.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:A pendulum clock keeping correct time is taken to high altitudes,
Explanation
Time period of pendulum,T = 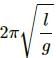
At higher altitudes, the value of acceleration due to gravity decreases. Therefore, the length of the pendulum should be decreased to compensate for the decrease in the value of acceleration due to gravity.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:The free end of a simple pendulum is attached to the ceiling of a box. The box is taken to a height and the pendulum is oscillated. When the bob is at its lowest point, the box is released to fall freely. As seen from the box during this period, the bob will
Explanation
As the acceleration due to gravity acting on the bob of pendulum, due to free fall gives a torque to the pendulum, the bob goes in a circular path.
Report a problem
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:Select the correct statements.
Explanation
A periodic motion need not be necessarily oscillatory. For example, the moon revolving around the earth. Also, an oscillatory motion need not be necessarily periodic. For example, damped harmonic motion.
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:A particle moves in a circular path with a uniform speed. Its motion is
Explanation
Because the particle covers one rotation after a fixed interval of time but does not oscillate around a mean position.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:A particle is fastened at the end of a string and is whirled in a vertical circle with the other end of the string being fixed. The motion of the particle is
Explanation
Because the particle completes one rotation in a fixed interval of time but does not oscillate around a mean position.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:A particle moves in a circular path with a continuously increasing speed. Its motion is
Explanation
As the particle does not complete one rotation in a fixed interval of time, neither does it oscillate around a mean position.
Report a problem
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:The motion of a torsional pendulum is
Explanation
Because it completes one oscillation in a fixed interval of time and the oscillations are in terms of rotation of the body through some angle.
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:Which of the following quantities are always negative in a simple harmonic motion?
Explanation
In S.H.M.,
F = -kx
Therefore,
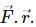 will always be negative. As acceleration has the same direction as the force,
will always be negative. As acceleration has the same direction as the force, 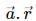 Will also be negative, always.
Will also be negative, always.
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:Which of the following quantities are always positive in a simple harmonic motion?
Explanation
As the direction of force and acceleration are always same,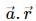 is always positive.
is always positive.
Report a problem
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:Which of the following quantities are always zero in a simple harmonic motion?
Explanation
As 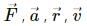 are either parallel or anti-parallel to each other, their cross products will always be zero.
are either parallel or anti-parallel to each other, their cross products will always be zero.
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:Suppose a tunnel is dug along a diameter of the earth. A particle is dropped from a point, a distance h directly above the tunnel. The motion of the particle as seen from the earth is
Explanation
If the particle were dropped from the surface of the earth, the motion of the particle would be SHM. But when it is dropped from a height h, the motion of the particle is not SHM because there is no horizontal velocity imparted. In that case, the motion of the particle would be periodic and in a straight line.
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:For a particle executing simple harmonic motion, the acceleration is proportional to
Explanation
For S.H.M.,
F = -kx
ma = - kx (F = ma)
or,
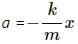
Thus, acceleration is proportional to the displacement from the mean position but in opposite direction.
Report a problem
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:A particle moves in the X-Y plane according to the equation 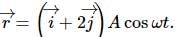 The motion of the particle is
The motion of the particle is
Explanation
The given equation is a solution to the equation of simple harmonic motion. The amplitude is 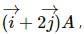 following equation of straight line y = mx + c. Also, a simple harmonic motion is periodic.
following equation of straight line y = mx + c. Also, a simple harmonic motion is periodic.
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:A particle moves on the X-axis according to the equation x = x0 sin2 ωt. The motion is simple harmonic
Explanation
Given equation:
x = xo sin2 ωt
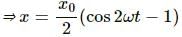
Now, the amplitude of the particle is xo/2 and the angular frequency of the SHM is 2ω.
Thus, time period of the SHM = 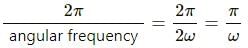
Report a problem
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:In a simple harmonic motion
Explanation
The kinetic energy of the motion is given as,
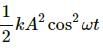
The potential energy is calculated as,
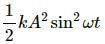
As the average of the cosine and the sine function is equal to each other over the total time period of the functions, the average potential energy in one time period is equal to the average kinetic energy in this period.
Report a problem
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:In a simple harmonic motion
Explanation
In SHM,
maximum kinetic energy = (1/2)kA2
maximum potential energy = (1/2)kA2
The minimum value of both kinetic and potential energy is zero.
Therefore, in a simple harmonic motion the maximum kinetic energy and maximum potential energy are equal. Also, the minimum kinetic energy and the minimum potential energy are equal.
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:An object is released from rest. The time it takes to fall through a distance h and the speed of the object as it falls through this distance are measured with a pendulum clock. The entire apparatus is taken on the moon and the experiment is repeated
Explanation
The effect of gravity on the object as well as on the pendulum clock is same in both cases; the time measured is also same. As the time measured is same, the speeds are same.
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 1
Try yourself:Which of the following will change the time period as they are taken to moon?
Explanation
As the time period of a simple pendulum and a physical pendulum depends on the acceleration due the gravity, the time period of these pendulums changes when they are taken to the moon.
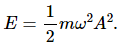 Which of the following two statements is more appropriate?
Which of the following two statements is more appropriate?The time period (T) of the pendulum becomes proportional to the square root of inverse of g if the length of the pendulum is kept constant.
where m is mass of the block, and k is the spring constant Time period is also given by the relation,
 The value of v is
The value of v is
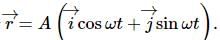 The motion of the particle is
The motion of the particle is

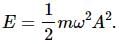 Suppose the oscillating particle is replaced by another particle of double the mass while the amplitude A remains the same. The new mechanical energy will
Suppose the oscillating particle is replaced by another particle of double the mass while the amplitude A remains the same. The new mechanical energy will
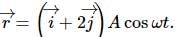 The motion of the particle is
The motion of the particle is







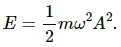
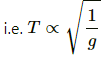
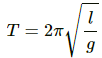
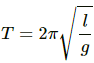
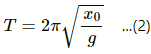
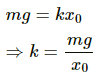
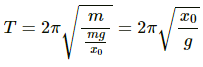
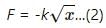
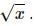
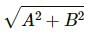
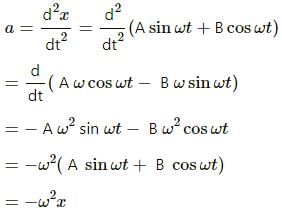
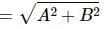
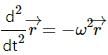
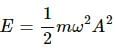
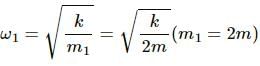
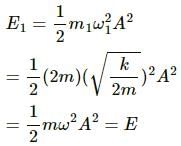
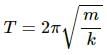
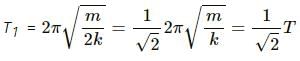
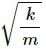
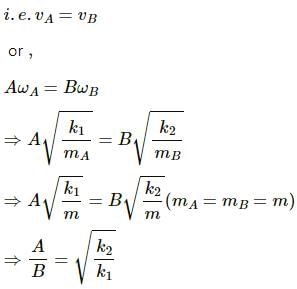
 of the system is independent of the acceleration of the system.
of the system is independent of the acceleration of the system.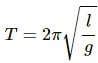
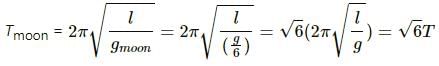
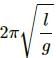
 will always be negative. As acceleration has the same direction as the force,
will always be negative. As acceleration has the same direction as the force, 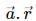 Will also be negative, always.
Will also be negative, always.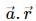 is always positive.
is always positive.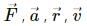 are either parallel or anti-parallel to each other, their cross products will always be zero.
are either parallel or anti-parallel to each other, their cross products will always be zero.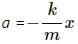
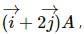 following equation of straight line y = mx + c. Also, a simple harmonic motion is periodic.
following equation of straight line y = mx + c. Also, a simple harmonic motion is periodic.