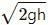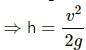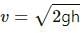Short Answers
Q.1. Is it always true that the molecules of a dense liquid are heavier than the molecules of a lighter liquid?
Density is defined as mass per unit volume. It tells how closely packed are the molecules inside an object. When molecules are tightly packed, we say that the object is dense; when molecules are far apart, we say that the object is light.
The density of a liquid depends on the mass of the molecules that make up the liquid and the closeness of the molecules of the liquid. It is not always true that the molecules of a dense liquid are heavier than the molecules of a lighter liquid.
For example, alcohol is less dense than oil. Alcohol molecules are mostly carbon and hydrogen atoms, so they are similar to oil. But they also contain an oxygen atom, which makes them a little heavy. For this reason, you might think that alcohol is denser than oil. But because of their shape and size, alcohol molecules do not pack as efficiently as oil molecules. This property of molecules makes alcohol less dense than oil.
Q.2. If someone presses a pointed needle against your skin, you are hurt. But if someone presses a rod against your skin with the same force, you easily tolerate. Explain.
We know that pressure is the application of force over a particular area. In mathematical terms, pressure is equal to force divided by area; that is, with more force comes more pressure and with more area comes less pressure. An iron rod has more surface area than the pointed tip of a needle. That is why the pointed needle exerts more pressure than the iron rod (with the same force) when pressed against our skin.
Q.3. In the derivation of P1 − P2 = ρgz, it was assumed that the liquid is incompressible. Why will this equation not be strictly valid for a compressible liquid?
In case of an incompressible liquid, the density is independent of the variations in pressure and always remains constant. But it is not so in case of a compressible liquid. Thus, the given equation will not be strictly valid for a compressible liquid.
Q.4. Suppose the density of air at Madras is ρo and atmospheric pressure is P0. If we go up, the density and the pressure both decrease. Suppose we wish to calculate the pressure at a height 10 km above Madras. If we use the equation Po − P = ρogz, will we get a pressure more than the actual or less than the actual? Neglect the variation in g. Does your answer change if you also consider the variation in g?
Using the equation Po − P = ρogz, we get:
P = Po − ρogz
The pressure calculated by using this equation will be more than the actual pressure because density at a height of 10 km above Madras will be less than ρo.
Yes, the answer will change if we also consider the variation in g. Because g decreases with height, it will have the same effect on pressure as that of density.
Q.5. The free surface of a liquid resting in an inertial frame is horizontal. Does the normal to the free surface pass through the centre of the earth? Think separately if the liquid is (a) at the equator (b) at a pole (c) somewhere else.
Yes, the normal to the free surface of the liquid passes through the centre of the Earth. Because of the gravitational force, the free surface of the liquid takes the shape of the surface of the Earth. Also, because the gravitational force is directed towards the centre of the Earth, the normal to the free surface also passes through the centre of the Earth (in all cases).
Q.6. A barometer tube reads 76 cm of mercury. If the tube is gradually inclined keeping the open end immersed in the mercury reservoir, will the length of mercury column be 76 cm, more than 76 cm or less than 76 cm?
The length of the mercury column will be more than 76 cm. The pressure depends on the height of the highest point of the mercury from the ground and not on the length of the liquid column.
Let:
l = Length of the mercury column
θ = Angle at which the tube is inclined with the vertical
Given : h = 76 cm
l cosθ = h
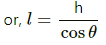
∴ l > h
Or,
l > 76 cm
Q.7. A one meter long glass tube is open at both ends. One end of the tube is dipped into a mercury cup, the tube is kept vertical and the air is pumped out of the tube by connecting the upper end to a suction pump. Can mercury be pulled up into the pump by this process?
No, mercury cannot be pulled up into the pump by this process. The level up to which mercury can rise is 76 cm (to maintain equal pressure at points A and B).
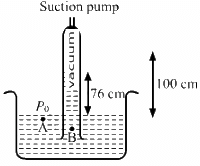
Q.8. A satellite revolves round the earth. Air pressure inside the satellite is maintained at 76 cm of mercury. What will be the height of mercury column in a barometer tube 1 m long placed in the satellite?
Pressure at point A is 76 cm of mercury. Therefore, mercury will rise to full length of the tube, i.e., 1 m, to maintain equal pressure at points A and B. Inside the satellite, geffective = 0, so the pressure due to height of the mercury column will be zero.
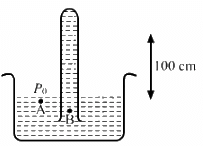
Q.9. Consider the barometer shown in the following figure. If a small hole is made at a point P in the barometer tube, will the mercury come out from this hole?
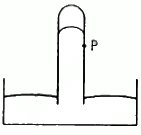
Two pressures are acting upon point P:
(1) Pressure due to mercury level above point P equals to P1 (say)
(2) Atmospheric pressure = P0 (inwards)
And,
P0 > P1
As the inward pressure is more, the mercury will not come out of the hole.
Q.10. Is Archimedes' principle valid in an elevator accelerating up ? In a car accelerating on a level road?
Archimedes' principle is not valid in case of an elevator accelerating upwards, but it is valid for a car accelerating on a level road.
According to Archimedes' principle,
Buoyant force, B = Weight of the substituted liquid
Or,
B = mg
The above principle is satisfied in case of a car accelerating on a level road.
In case of an elevator, the buoyant force will be as below:
B = mg + ma (If the elevator is going upwards with an acceleration a)
Thus, Archimedes' principle is not valid in this case.
Q.11. Why is it easier to swim in sea water than in fresh water?
Whether an object sinks or floats in a liquid depends upon the density of the two. We know that sea water has dissolved salts in it, which increase its density. So, sea water exerts more buoyancy force (in the upward direction) on the swimmer than that exerted by fresh water. This helps the person to swim easily in sea water compared to fresh water.
Q.12. A glass of water has an ice cube floating in water. The water level just touches the rim of the glass. Will the water overflow when the ice melts?
The water of mass equal to the mass of the ice cube will take less volume compared to the ice cube. The water will not overflow when the ice melts because the ice will displace the space it would take if it were in a liquid state.
Q.13. A ferry boat loaded with rocks has to pass under a bridge. The maximum height of the rocks is slightly more than the height of the bridge so that the boat just fails to pass under the bridge. Should some of the rocks be removed or some more rocks be added?
Some rocks should be added to increase the force acting in the downward direction. It will help the boat to pass under the bridge. If some rocks are removed, the upthrust of water on the boat will be greater than the weight of the boat. So, the boat will rise in water and will fail to pass under the bridge.
Q.14. Water is slowly coming out from a vertical pipe. As the water descends after coming out, its area of cross section reduces. Explain this on the basis of the equation of continuity.
Let a be the area of cross section and v be the velocity of water.
According to the equation of continuity,
av = Constant
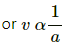
It means the larger the area of cross section, the smaller will be the velocity of liquid and vice versa.
Thus, as the water comes out of the vertical pipe, its velocity increases and area of cross section decreases.
Q.15. While watering a distant plant, a gardener partially closes the exit hole of the pipe by putting his finger on it. Explain why this results in the water stream going to a larger distance.
According to the equation of continuity, if the exit hole of the pipe is partially closed, the water stream comes out with more velocity due to decrease in area. This results in the water stream going to a larger distance.
Q.16. A Gipsy car has a canvass top. When the car runs at high speed, the top bulges out. Explain.
This can be explained through Bernoulli's principle, which states that the higher the air speed, the lower the pressure in that area. Because the air inside the car does not move, the pressure in the car is atmospheric. Because air moves outside the car (directly above it), the pressure is low. The canvas top of the Gipsy car is pushed upwards because the pressure inside the car is greater than the pressure directly above the car.
Multiple Choice Questions
Question for HC Verma Questions and Solutions: Chapter 13: Fluid Mechanics- 1
Try yourself:A liquid can easily change its shape but a solid can not because
Explanation
The forces between the molecules is stronger in solids than in liquids. The forces between the particles of a solid are stronger than those between the particles of a liquid, so the particles cannot move freely but can only vibrate. Thus, a solid has stable, definite shape and volume. A solid can only change its shape by force (when broken or cut), whereas a liquid can easily change its shape because of weak inter-particle forces.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 13: Fluid Mechanics- 1
Try yourself:Consider the equations 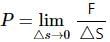 and P1 - P2 = pgz. In an elevator accelerating upward
and P1 - P2 = pgz. In an elevator accelerating upward
Explanation
For a point inside the elevator, pressure can be defined as 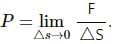 It is independent of the acceleration of the elevator. The modified form of the second equation, which will be valid in the given case, is given by P1 - P2 = ρ(g+a0)z. Here, acceleration a0 (say) due to elevator accelerating upwards is also taken into account.
It is independent of the acceleration of the elevator. The modified form of the second equation, which will be valid in the given case, is given by P1 - P2 = ρ(g+a0)z. Here, acceleration a0 (say) due to elevator accelerating upwards is also taken into account.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 13: Fluid Mechanics- 1
Try yourself:The three vessels shown in the following figure have same base area. Equal volumes of a liquid are poured in the three vessels. The force on the base will be

Explanation
Here, the height of the liquid column is maximum in vessel C. Thus, the force on the base of vessel C, i.e., F = P0 + hρg where P0 is atmospheric pressure, is maximum.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 13: Fluid Mechanics- 1
Try yourself:Equal mass of three liquids are kept in three identical cylindrical vessels A, B and C. The densities are ρA, ρB, ρC with ρA < ρB < ρC. The force on the base will be
Explanation
The force on the base is given by
F = hρg × A
⇒ F = (hAρ)g
⇒ F = (Volume ×Density) × g
⇒ F = mg}
In the question, the masses are equal. So, the force on the base is the same in all cases.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 13: Fluid Mechanics- 1
Try yourself:Shows in the following figure a siphon. The liquid shown is water. The pressure difference PB − PA between the points A and B is
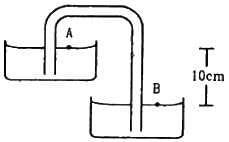
Explanation
At both points A and B, pressure is equal to atmospheric pressure.
Thus, we have :
PA = PB = Patm
⇒ PB - PA = 0
Report a problem
Question for HC Verma Questions and Solutions: Chapter 13: Fluid Mechanics- 1
Try yourself:A beaker containing a liquid is kept inside a big closed jar. If the air inside the jar is continuously pumped out, the pressure in the liquid near the bottom of the liquid will
Explanation
As the air inside the jar is pumped out, the air pressure decreases. Thus, the pressure in the liquid near the bottom of the beaker decreases.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 13: Fluid Mechanics- 1
Try yourself:The pressure in a liquid at two points in the same horizontal plane are equal. Consider an elevator accelerating upward and a car accelerating on a horizontal road. The above statement is correct in
Explanation
The two points in the same horizontal line will not have equal pressure if the liquid is accelerated horizontally. There should be vertical acceleration.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 13: Fluid Mechanics- 1
Try yourself:Suppose the pressure at the surface of mercury in a barometer tube is P1 and the pressure at the surface of mercury in the cup is P2.
Explanation
The upper part of the tube contains vacuum as the mercury goes down and no air is allowed in. Thus, the pressure at the upper end, i.e., at the surface of mercury in a barometer tube is zero (P1 = 0). However, the pressure at the surface of mercury in the cup or any another point at the same horizontal plane is equal to the atmospheric pressure.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 13: Fluid Mechanics- 1
Try yourself:A barometer kept in an elevator reads 76 cm when it is at rest. If the elevator goes up with increasing speed, the reading will be
Explanation
If the elevator goes up at an increasing speed, then the effective value of g increases.
We know:
P = ρgh
So, h will have a lesser value for the same value of P if g increases.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 13: Fluid Mechanics- 1
Try yourself:A barometer kept in an elevator accelerating upward reads 76 cm. The air pressure in the elevator is
Explanation
When the elevator is going upwards with acceleration a, the effective acceleration is a' =(g + a).
Thus, pressure is given by
P = hρ(g + a)
Air pressure in the elevator = P = h'ρg
Because the pressure is the same, h' > h.
∴ Air pressure > 76 cm
Report a problem
Question for HC Verma Questions and Solutions: Chapter 13: Fluid Mechanics- 1
Try yourself:To construct a barometer, a tube of length 1 m is filled completely with mercury and is inverted in a mercury cup. The barometer reading on a particular day is 76 cm. Suppose a 1 m tube is filled with mercury up to 76 cm and then closed by a cork. It is inverted in a mercury cup and the cork is removed. The height of mercury column in the tube over the surface in the cup will be
Explanation
Because of the trapped air, the pressure at the upper end of the mercury column inside the tube is not zero.
In other words, P0 > 0.
Using this relation, we get:
Patm = P0 + ρgh
Here,
ρ = Density of mercury
h = Height of the mercury column
∵ P0 > 0
And,
Patm > ρgh
∴ 76 cm of Hg >ρgh
or, h < 76 cm
Report a problem
Question for HC Verma Questions and Solutions: Chapter 13: Fluid Mechanics- 1
Try yourself:A 20 N metal block is suspended by a spring balance. A beaker containing some water is placed on a weighing machine which reads 40 N. The spring balance is now lowered so that the block gets immersed in the water. The spring balance now reads 16 N. The reading of the weighing machine will be
Explanation
Upthrust exerted by the water on the block = Change in the reading of the spring balance
= (20 − 16) N = 4 N
Downthrust = 4 N
Actual weight of the beaker containing water = 40 N
∴ Effective weight = (40 + 4) N = 44 N
Report a problem
Question for HC Verma Questions and Solutions: Chapter 13: Fluid Mechanics- 1
Try yourself:A piece of wood is floating in water kept in a bottle. The bottle is connected to an air pump. Neglect the compressibility of water. When more air is pushed into the bottle from the pump, the piece of wood will float with
Explanation
When more air is pushed into the bottle from the pump, the pressure of air increases on the wood as well as on the water surface with the same amount. So, the level of water and wood does not change. Thus, the piece of wood floats with the same part in the water.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 13: Fluid Mechanics- 1
Try yourself:A metal cube is placed in an empty vessel. When water is filled in the vessel so that the cube is completely immersed in the water, the force on the bottom of the vessel in contact with the cube
Explanation
In the absence of water, the force acting on the bottom of the vessel is due to the air and the cube. Now, when water is filled in the vessel, the force due to the water and the cube is greater. The extra force is balanced by the buoyant force acting on the cube in the upward direction
Report a problem
Question for HC Verma Questions and Solutions: Chapter 13: Fluid Mechanics- 1
Try yourself:A wooden object floats in water kept in a beaker. The object is near a side of the beaker . Let P1, P2, P3 be the pressures at the three points A, B and C of bottom as shown in the figure.
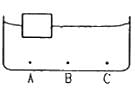
Explanation
If the fluid is in equilibrium, then the pressure is the same at all points in the same horizontal level.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 13: Fluid Mechanics- 1
Try yourself:A closed cubical box is completely filled with water and is accelerated horizontally towards right with an acceleration α. The resultant normal force by the water on the top of the box
Explanation
When the box is accelerated towards right, the water in the box experiences a pseudo force (ma) towards left, where m is the mass of water. So, the resultant normal force by the water on the top of the box passes through a point to the left of the centre.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 13: Fluid Mechanics- 1
Try yourself:Consider the situation of the previous problem. Let the water push the left wall by a force F1 and the right wall by a force F2.
Explanation
When the box is accelerated towards right, the water in the box experiences a pseudo force (ma) towards left, where m is the mass of water. So, the force F1 exerted by the water on the the left wall of the box is greater.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 13: Fluid Mechanics- 1
Try yourself:Water enters through end A with a speed v1 and leaves through end B with a speed v2 of a cylindrical tube AB. The tube is always completely filled with water. In case I the tube is horizontal, in case II it is vertical with the end A upward and in case III it is vertical with the end B upward. We have v1 = v2 for
Explanation
This happens in accordance with the equation of continuity. As the area of the cross section of cylindrical tube AB is constant, the velocity of water will also be the same. The equation is derived from the principle of conservation of mass and it is true for every case, i.e., when the tube is either horizontal or vertical.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 13: Fluid Mechanics- 1
Try yourself:Bernoulli theorem is based on the conservation of
Explanation
Bernoulli’s theorem states that, in a steady flow, the sum of all forms of energy in a fluid along a streamline is the same at all points on that streamline. Thus, energy is conserved in Bernoulli’s theorem.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 13: Fluid Mechanics- 1
Try yourself:Water is flowing through a long horizontal tube. Let PA and PB be the pressures at two points A and B of the tube.
Explanation
According to Bernoulli's theorem, pressures at points A and B of the horizontal tube will be equal if water has the same velocity at these points. Also, according to the equation of continuity, velocity at points A and B will be equal only if the cross-sectional areas at A and B are equal. So, PA = PB only if the cross-sectional areas at A and B are equal.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 13: Fluid Mechanics- 1
Try yourself:Water and mercury are filled in two cylindrical vessels up to same height. Both vessels have a hole in the wall near the bottom. The velocity of water and mercury coming out of the holes are v1 and v2 respectively.
Explanation
The velocity of efflux does not depend on the density of the liquid. It only depends on the height h (given same in the question) and acceleration due to gravity g (constant value here).
v1 = v2 = v = 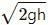
Report a problem
Question for HC Verma Questions and Solutions: Chapter 13: Fluid Mechanics- 1
Try yourself:A large cylindrical tank has a hole of area A at its bottom. Water is poured in the tank by a tube of equal cross-sectional area A ejecting water at the speed v.
Explanation
The water level will rise to a height v2/2g and then stop.
From the principle of continuity and Bernoulli's equation, we have:
v2 = 2gh
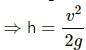
So, h is the maximum height up to which the water level will rise if the water is ejected at a speed v.
Report a problem
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 13: Fluid Mechanics- 1
Try yourself:A solid floats in a liquid in a partially dipped position.
Explanation
Force exerted by any solid on a liquid = F = mg = W = Weight of the solid
According to Archimedes' principle, any object, wholly or partially immersed in a fluid, is buoyed up by a force equal to the weight of the fluid displaced by the object.
Also, any floating object displaces its own weight of fluid. Thus, we can say that the weight of the object is equal to the weight of the fluid displaced.
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 13: Fluid Mechanics- 1
Try yourself:The weight of an empty balloon on a spring balance is W1. The weight becomes W2 when the balloon is filled with air. Let the weight of the air itself be w. Neglect the thickness of the balloon when it is filled with air. Also neglect the difference in the densities of air inside and outside the balloon.
Explanation
According to the question, the density of air inside and outside the balloon is the same. So, the weight w of air inside the balloon is equal to the weight of displaced air. Thus, the spring balance will not register any difference because the balloon will experience buoyant force equal to w that cancels out the weight of the added air.
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 13: Fluid Mechanics- 1
Try yourself:A solid is completely immersed in a liquid. The force exerted by the liquid on the solid will
Explanation
The force exerted by the liquid on the solid is the vertically upward force (buoyant force) that opposes the weight of the immersed solid. As more and more volume of the solid is immersed in the liquid, the buoyant force increases.
Buoyant force depends on the weight of the displaced liquid. So, maximum upward buoyant force acts on the solid when it is completely immersed in the liquid. It decreases if the solid is taken partially out of the liquid. Once the object is immersed in the liquid, then pushing it further in the liquid does not increase the buoyant force.
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 13: Fluid Mechanics- 1
Try yourself:A closed vessel is half filled with water. There is a hole near the top of the vessel and air is pumped out from this hole.
Explanation
As air is pumped out of the hole, there is a decrease in the atmospheric pressure above the water surface in the vessel. Due to this, pressure at the surface of the water decreases. Thus, the force exerted by the water on the bottom of the vessel also decreases.
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 13: Fluid Mechanics- 1
Try yourself:In a streamline flow,
Explanation
In a streamline flow, every fluid particle arriving at a given point has the same velocity v. Thus, the kinetic energies (1/2 mv2) and momenta (mv) of all particles arriving at a given point are the same, as the mass of a particle is constant.
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 13: Fluid Mechanics- 1
Try yourself:Water flows through two identical tubes A and B. A volume V0 of water passes through the tube A and 2 V0 through B in a given time. Which of the following may be correct?
Explanation
In a steady flow, the velocity of liquid particles reaching a particular point is the same at all times, but if the liquid is pushed in the tube at a rapid rate, i.e., if the flow rate increases, then the flow may become turbulent. Here, the flow rate is the volume of fluid per unit time per unit area flowing past a point.
Large volume of water passes through tube B compared to tube A. Thus, the flow rate is greater in tube B than in tube A. So, if the flow is turbulent in A, then the flow in B cannot be steady. Therefore, the first three options are possible
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 13: Fluid Mechanics- 1
Try yourself:Water is flowing in streamline motion through a tube with its axis horizontal. Consider two points A and B in the tube at the same horizontal level.
Explanation
In streamline flow in a tube, every particle of the liquid follows the path of its preceding particle and the velocity of all particles crossing a particular point is the same. However, the velocity of the particles at different points in their path may not necessarily be the same. Thus, by applying Bernoulli's theorem and equation of continuity, we can say that if the tube has a uniform cross section, the pressures will be equal; and if the tube has a non-uniform cross section, the pressures may or may not be equal.
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 13: Fluid Mechanics- 1
Try yourself:There is a small hole near the bottom of an open tank filled with a liquid. The speed of the water ejected does not depend on
Explanation
The emergent speed v of the liquid flowing from the hole in the bottom of the tank is given by 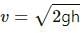
Here, g is acceleration due to gravity and h is height of the liquid from the hole.
Thus, it is clear from the above relation that the speed of the liquid depends on the height of the liquid from the hole and on the acceleration due to gravity. It does not depend on the area of the hole and the density of the liquid.

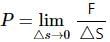 and P1 - P2 = pgz. In an elevator accelerating upward
and P1 - P2 = pgz. In an elevator accelerating upward




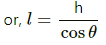


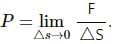 It is independent of the acceleration of the elevator. The modified form of the second equation, which will be valid in the given case, is given by P1 - P2 = ρ(g+a0)z. Here, acceleration a0 (say) due to elevator accelerating upwards is also taken into account.
It is independent of the acceleration of the elevator. The modified form of the second equation, which will be valid in the given case, is given by P1 - P2 = ρ(g+a0)z. Here, acceleration a0 (say) due to elevator accelerating upwards is also taken into account.