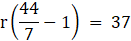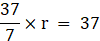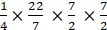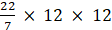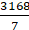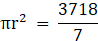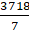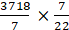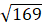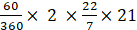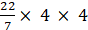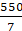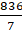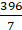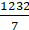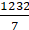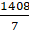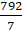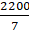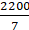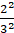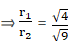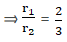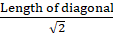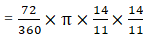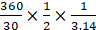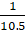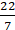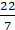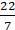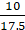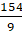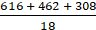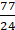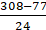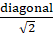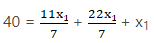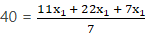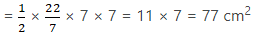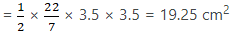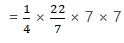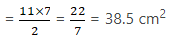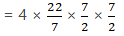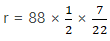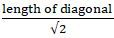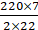RS Aggarwal Solutions: Area of Circle, Sector and Segment- 1 - Class 10 PDF Download
Exercise: 18a
Q.1. The difference between the circumference and radius of a circle is 37 cm. Using π = 22/7, find the circumference of the circle.
Given:
Difference between the circumference and the radius of circle = 37 cm
Let the radius of the circle be ‘r’.
Circumference of the circle = 2πr
So, Difference between the circumference and the radius of the circle = 2πr – r = 37
2πr – r = 37
2 × (22/7) × r – r = 37
(44/7) × r – r = 37
r = 37 × (7/37)
r = 7 cm
∴ Circumference of circle = 2 × (22/7) × 7
= 2 × 22
= 44 cm
Hence the circumference of the circle is 44 cm.
Q.2. The circumference of a circle is 22 cm. Find the area of its quadrant.
Given:
Circumference of circle = 22 cm
Let the radius of the circle be ‘r’.
∵ Circumference of circle = 2πr
∴ 22 = 2 × π × r
⇒ 22 = 2 × (22/7) × r
⇒ 22 × (7/22) × (1/2) = r or = r
or r = (7/2)
∵ Area of circle = πr2
∴ Area of its quadrant = (1/4)πr2
=
= 77/8
Hence the area of the quadrant of the circle is 77/8 cm.
Q.3. What is the diameter of a circle whose area is equal to the sum of the areas of two circles of diameter 10 cm and 24 cm?
Given:
Let the two circles be C1 and C2 with diameters 10 cm and 24 cm respectively.
Area of circle, C = Area of C1 + Area of C2 …… (i)
∵ Diameter = 2 × radius
∴ Radius of C1, r1 = 10/2 = 5cm
and Radius of C2, r2 = 24/2 = 12cm
∵ Area of circle = πr2 …… (ii)
∴ Area of C1 = πr12
= (22/7) 5 x 5
= (22/7) x 25
= 550/7 cm2
Similarly, Area of C2 = πr22
=
= 22/7 × 144
= 3168/7 cm2
∴ Using equation (i), we have
Area of C =+
=cm2
Now, using equation (ii), we have× r2 =
r2 =
r2 = 169
r =
r = 13 cm
⇒ Diameter = 2 × r
= 2 × 13
= 26 cm
Hence, the diameter of the circle is 26 cm.
Q.4. If the area of a circle is numerically equal to twice its circumference, then what is the diameter of the circle?
Given:
Area of circle = 2 × Circumference of circle …… (i)
Let the radius of the circle be ‘r’.
Then, the area of the circle = πr2
and the circumference of the circle = 2πr
Using (i), we have
πr2 = 2 × 2πr
πr2 = 4πr
r = 4 cm
∵ Diameter = 2 × radius
∴ Diameter = 2 × 4
= 8 cm
Hence, the diameter of the circle is 8 cm.
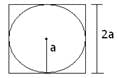
Q.5. What is the perimeter of a square which circumscribes a circle of radius a cm?
Given:
Perimeter of square circumscribes a circle of radius ‘a’.
Side of square = Diameter of circle
Diameter of circle = 2 × radius
= 2a
So, Side of square = 2a
∵ Perimeter of square = 4 × side
∴ Perimeter of square = 4 × 2a
= 8a
Hence, the perimeter of the square is 8a.
Q.6. Find the length of the arc of a circle of diameter 42 cm which subtends an angle of 60° at the centre.
Given:
Diameter of circle = 42 cm
⇒ Radius of circle = 42/2 cm = 21 cm
Angle subtended at the centre = 60°
∵ Length of arc =× 2πr
=
= 22 cm
Hence, the length of the arc is 22 cm.
Q.7. Find the diameter of the circle whose area is equal to the sum of the areas of two circles having radii 4 cm and 3 cm.
Given:
Let the two circles with radii 4 cm and 3 cm be C1 and C2 respectively.
⇒ r1 = 4 cm and r2 = 3 cm
Area of circle, C = Area of C1 + Area of C2 …… (i)
∵ Area of circle = πr2 …… (ii)
∴ Area of C1 = πr12=
=× 16 =
cm2
Similarly, Area of C2 = πr22
=× 3 × 3
=× 9 =
cm2
So, using (i), we have
Area of C =+
=
cm2
Now, using (ii), we have
πr2 = 550/7× r2 =
r2 =×
= 25
r = √25 = 5
r = 5 cm
∵ Diameter = 2 × radius
∴ Diameter = 2 × 5 = 10 cm
Hence, diameter of the circle with area equal to the sum of two circles of radii 4 cm and 3cm is 10 cm.
Q.8. Find the area of a circle whose circumference is 8π.
Given:
Circumference of circle = 8π
∵ Circumference of a circle = 2πr
∴ 8π = 2πr
r = 4
∵ Area of circle = πr2
∴ Area of circle = π × 4 × 4
= 16π
Hence, the area of the circle is 16π.
Q.9. Find the perimeter of a semicircular protractor whose diameter is 14 cm.
Given:
Diameter of the semicircular protractor = 14 cm
Radius of the protractor = 14/2 cm = 7cm
∵ Perimeter of semicircle = πr + d
∴ Perimeter of semicircular protractor = (22/7)× 7 + 14 = 22 + 14
= 36 cm
Hence, the perimeter of the semicircular protractor is 36 cm.
Q.10. Find the radius of a circle whose perimeter and area are numerically equal.
Given:
Perimeter of circle = Area of circle …… (i)
∵ Perimeter of circle = 2πr and Area of circle = πr2
∴ Using (i), we have
2πr = πr2
2 = πr2/2πr
2 = r or r = 2
Hence, the radius of the circle is 2 cm.
Q.11. The radii of two circles are 19 cm and 9 cm. Find the radius of the circle which has circumference equal to the sum of the circumferences of the two circles.
Given:
Radius of one of the circles, C1 = 19 cm = r1
Radius of the other circle, C2 = 9 cm = r2
Let the other circle be C with radius ‘r’.
Circumference of C = Circumference of C1 + Circumference of C2 …………(i)
∵ Circumference of circle = 2πr
∴ Circumference of C1 = 2πr1 = 2 ×× 19 =
and Circumference of C2 = 2πr2 = 2 ×× 9 =
Using (i), we have
2πr =+
=
2 ×× r =
r =×
×
= 28
r = 28 cm
Hence, the radius of the circle is 28 cm.
Q.12. The radii of two circles are 8 cm and 6 cm. Find the radius of the circle having area equal to the sum of the areas of the two circles.
Given:
Radius of one of the circles, C1 = 8 cm = r1
Radius of the other circle, C2 = 6 cm = r2
Let the other circle be C with radius ‘r’.
Area of C = Area of C1 + Area of C2 …… (i)
∵ Area of circle = πr2
∴ Area of C1 = πr12 =× 8 × 8 =
and Area of C2 = πr22 =× 6 × 6 =
Using (i), we have
πr2 =+
=
× r2 =
r2 =×
= 100
r2 = 100
r = √100 = 10 or r = 10
Hence, the radius of the circle is 10 cm.
Q.13. Find the area of the sector of a circle having radius 6 cm and of angle 30°.
Given:
Radius of circle = 6 cm
Angle of the sector = 30°
∵ Area of sector =× πr2
=× 3.14 × 6 × 6
= 3 × 3.14 = 9.42 cm2
Hence, the area of the sector is 9.42 cm2.
Q.14. In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the length of the arc.
Given:
Radius of circle = 21 cm
Angle subtended by the arc = 60°
∵ Length of arc =× 2πr
=× 2 ×
× 21 = 22 cm
Hence, the length of the arc is 22 cm.
Q.15. The circumferences of two circles are in the ratio 2:3. What is the ratio between their areas?
Given:
Ratio of circumferences of two circles = 2:3
Let the two circles be C1 and C2 with radii ‘r1’ and ‘r2’.
∵ Circumference of circle = 2πr
∴ Circumference of C1 = 2πr1
and Circumference of C2 = 2πr2
⇒=
⇒=
Squaring both sides, we get
⇒=
Multiplying both sides by ‘π’, we get
⇒=
∵ Area of circle = πr2
⇒=
Hence, the ratio between the areas of C1 and C2 is 4:9.
Q.16. The areas of two circles are in the ratio 4:9. What is the ratio between their circumferences?
Given:
Ratio of areas of two circles = 2:3
Let the two circles be C1 and C2 with radii ‘r1’ and ‘r2’.
∵ Area of circle = πr2
∴ Area of C1 = πr12
and Area of C2 = πr22
⇒=
⇒=
Taking square root on both sides, we get
Multiplying and dividing L.H.S. by ‘π’, we get
Multiplying and dividing L.H.S. by ‘2’, we get
⇒=
As Circumference of circle = 2πr
⇒=
Hence, the ratio between the circumferences of C1 and C2 is 2:3.
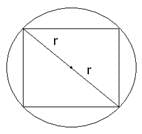
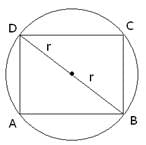
Q.17. A square is inscribed in a circle. Find the ratio of the areas of the circle and the square.
Given:
A square is inscribed in a circle.
Let the radius of circle be ‘r’ and the side of the square be ‘x’.
⇒ The length of the diagonal = 2r
∵ Length of side of square =
∴ Length of side of square == √2r
Area of square = side × side = x × x = √2r × √2r = 2r2
Area of circle = πr2
Ratio of areas of circle and square ==
=
Hence, the ratio of areas of circle and square is π:2.
Q.18. The circumference of a circle is 8 cm. Find the area of the sector whose central angle is 72°.
Given:
Circumference of circle = 8 cm
Central angle = 72°
∵ Circumference of a circle = 2πr
∴ 2πr = 8
2 ×× r = 8
r = 8 ××
r =cm
∵ Area of sector =× πr2
= 1.02 cm2
Q.19. A pendulum swings through an angle of 30° and describes an arc 8.8 cm in length. Find the length of the pendulum.
Given:
Angle made by the pendulum = 30°
Length of the arc made by the pendulum = 8.8 cm
Then the length of the pendulum is equal to the radius of the sector made by the pendulum.
Let the length of the pendulum be ‘r’.
∵ Length of arc =× 2πr
∴ We have,× 2πr = 8.8
(30/360) × 2 × 3.14 × r = 8.8
r = 8.8 ×
r = 16.8 cm
Hence, the length of the pendulum is 16.8 cm.
Q.20. The minute hand of a clock is 15 cm long. Calculate the area swept by it in 20 minutes.
Given:
Length of minute hand = 15 cm
Here, the length of the minute hand is equal to the radius of the sector formed by the minute hand.
Angle made by the minute hand in 1 minute = 360/60 = 6°
Angle made by the minute hand in 20 minutes = 20 × 6 = 120°
Here, the area swept by the minute hand is equal to the area of the corresponding sector made.
∵ Area of sector = (θ/360) x πr2
= (120/360) × 3.14 × 15 × 15 = 235.5 cm2
Hence, the area swept by it in 20 minutes is 235.5 cm2.
Q.21. A sector of 56°, cut out from a circle, contains 17.6 cm2. Find the radius of the circle.
Given:
Angle of the sector = 56°
Area of the sector = 17.6 cm2
Let the radius of the circle be ‘r’.
∵ Area of sector =× πr2
∴ 17.6 =×
× r2
r2 =×
× 17.6
r2 = 36
r = √36
r = 6 cm
Hence, the radius of the circle is 6 cm.
Q.22. The area of the sector of a circle of radius 10.5 cm is 69.3 cm2. Find the central angle of the sector.
Given:
Radius of the circle = 10.5 cm
Area of the sector = 69.3 cm2
∵ Area of the sector =× πr2
∴ 69.3 =×
× 10.5 × 10.5
θ = 69.3 × 360 ××
×
θ = 72°
Hence, the central angle is 72°.
Q.23. The perimeter of a certain sector of a circle of radius 6.5 cm is 31 cm. Find the area of sector.
Given:
Radius of circle = 6.5 cm
Perimeter of sector = 31 cm
Now, Perimeter of sector = 2 × radius + Length of arc
∵ Length of arc =× 2r × 2πr
∴ Perimeter of sector = 2 × r +× 2r × π
= 2r × [1 +× π]
31 = 2 × 6.5 × [1 +×
]
31 = 13 × [1 +×
]
= 1 +
×
- 1 =
×
=
×
θ =× 360 ×
…. (i)
∵ Area of sector =× πr2
∴ using (i), we have
Area =× 360 ×
×
×
× 6.5 × 6.5
= 18 × 3.25 = 58.5 cm2
Hence, the area of the sector is 58.5 cm2.
Q.24. The radius of a circle is 17.5 cm. Find the area of the sector enclosed by two radii and an arc 44 cm in length.
Given:
Radius of circle = 17.5 cm
Length of arc = 44 cm
∵ Length of arc =× 2πr
∴ 44 =× 2 ×
× 17.5
θ = 44 × 360 ××
×
θ == 144°
Now, Area of sector =× πr2
=×
× 17.5 × 17.5 = 385 cm2
Hence, the area of the sector is 385 cm2.
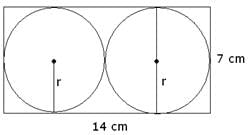
Q.25. Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular cardboard of dimensions 14 cm × 7 cm. Find the area of the remaining cardboard.
Given:
Length of the rectangular cardboard = 14 cm
Breadth of the rectangular cardboard = 7 cm
∵ Area of rectangle = length × breadth
∴ Area of cardboard = 14 × 7 = 98 cm2
Let the two circles with equal radii and maximum area have a radius of ‘r’ cm each.
Then, 2r = 7
r = 7/2 cm
∵ Area of circle = πr2
∴ Area of two circular cut outs = 2 × πr2
= 2 ××
×
= 11 × 7 = 77 cm2
Thus, the area of remaining cardboard = 98 – 77 = 21 cm2
Hence, the area of remaining cardboard is 21 cm2.
Q.26. In the given figure, ABCD is a square of side 4 cm. A quadrant of a circle of radius 1 cm is also drawn. Find the area of the shaded region.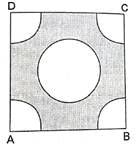
Given:
Side of the square = 4 cm
Radius of the quadrants at the corners = 1 cm
Radius of the circle in the centre = 1 cm
∵ 4 quadrants = 1 circle
∴ There are 2 circles of radius 1 cm
Area of square = side × side
= 4 × 4 = 16 cm2
Area of 2 circles = 2 × πr2
= 2 ×× 1 × 1 =
cm2
∵ Area of shaded region = Area of square – Area of 2 circles
= 16 - (44/7)
==
cm2 = 9.7 cm2
Hence, the area of shaded region is 9.72 cm2.
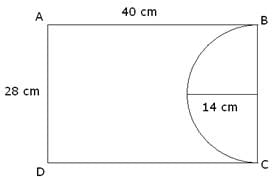
Q.27. From a rectangular sheet of paper ABCD wit AB = cm and AD = 28 cm, a semicircular portion wit BC as diameter is cut off. Find the area of the remaining paper.
Given:
Length of rectangular sheet of paper = 40 cm
Breadth of rectangular sheet of paper = 28 cm
Radius of the semicircular cut out = 14 cm
∵ Area of rectangle = length × breadth
∴ Area of rectangular sheet of paper = 40 × 28
= 1120 cm2
∵ Area of semicircle = (1/2)πr2
∴ Area of semicircular cut out =×
× 14 × 14
= 22 × 14 = 308 cm2
Thus, the area of remaining sheet of paper = Area of rectangular sheet of paper – Area of semicircular cut out
= 1120 – 308 = 812 cm2
Hence, the area of remaining sheet of paper is 812 cm2.
Q.28. In the given figure, OABC is a square of side 7 cm. If COPB is a quadrant of a circle wit centre C find the area of the shaded region.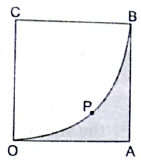
Given:
Side of square = 7 cm
Radius of the quadrant = 7 cm
Area of square = side × side
= 7 × 7 = 49 cm2
∵ Area of circle = πr2
∴ Area of a quadrant = (1/4) πr2
=×
× 7 × 7
= 77/2 = 38.5 cm2
Thus, the area of shaded region = Area of square – Area of quadrant
= 49 – 38.5 = 10.5 cm2
Hence, the area of the shaded region is 10.5 cm2.
Q.29. In the given figure, three sectors of a circle of radius 7 cm, making angles of 60°, 80° and 40° at the centre are shaded. Find the area of the shaded region.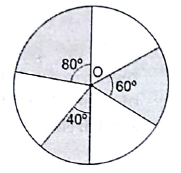
Given:
Radius of circle = 7 cm
Let the sectors with central angles 80°, 60° and 40° be S1, S2, and S3 respectively.
Then, the area of shaded region = Area of S1 + Area of S2 + Area of S3 ... (i)
∵ Area of sector = (θ/360) × πr2
∴ Area of S1 =×
× 7 × 7
= (308/9) cm2
Similarly, Area of S2 =×
× 7 × 7
= 154/6 cm2
and Area of S3 =×
× 7 × 7
= 154/9 cm2
Thus, using (i), we have
Area of shaded region =+
+
=
= 1386/18 = 77cm2
Hence, the area of shaded region is 77 cm2.
Q.30. In the given figure, PQ and AB are respectively the arcs of two concentric circles of radii 7 cm and 3.5 cm with centre O. If ∠POQ = 30°, find the area of the shaded region.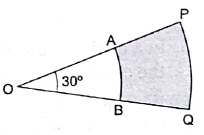
Given:
Radius of inner circle = 3.5 cm
Radius of outer circle = 7 cm
∠POQ = 30°
Let the sector made by the arcs PQ and AB be S1 and S2 respectively.
Then, Area of shaded region = Area of S1 – Area of S2 ….(i)
∵ Area of sector = (θ/360) x πr2
∴ Area of S1 =×
× 7 × 7
= 71/6 cm2
Similarly, Area of S2 =×
× 3.5 × 3.5
= 77/24 cm2
Thus, using (i), we have
Area of shaded region =-
=
==
cm2
Hence, the area of shaded region is 77/8 cm2.
Q.31. In the given figure, find the area of the shaded region, if ABCD is a square of side 14 cm and APD and BPC are semicircle.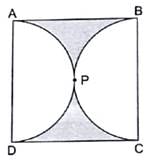
Given:
Side of square = 14 cm
Diameter of each semicircle = 14 cm
Radius of each semicircle = 14/2 = 7 cm
∵ Both the semicircles have same radius.
∴ We consider one circle of radius 7 cm.
Area of shaded region = Area of square – Area of circle …. (i)
Area of square = side × side
= 14 × 14 = 196 cm2
Area of circle = πr2
= 22/7 × 7 × 7 = 22 × 7 = 154 cm2
Thus, using (i), we have
Area of shaded region = 196 – 154 = 42 cm2
Hence, the area of shaded region is 42 cm2.
Q.32. In the given figure, the shape of the top of a table is that of a sector of circle with centre O and ∠AOB = 90°. If AO = OB = 42 cm, then find the perimeter of the top of the table.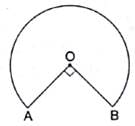
Give:
Radius of the circle = 42 cm
Central angle of the sector = ∠AOB = 90°
Perimeter of the top of the table = Length of the major arc AB + 2 × radius ……. (i)
Length of major arc AB =× 2πr
=× 2 ×
× 42
= (270/360) × 2 × 22 × 6
= 3/4 × 264 = 3 × 66 = 198 cm
Thus, using (i), we have
Perimeter of the top of the table = 198 + 2 × 42
= 198 + 84 = 282 cm
Hence, the perimeter of the top of the table is 282 cm.
Q.33. In the given figure, ABCD is a square of side 7 cm, DPBA and DQBC are quadrants of circles each of the radius 7 cm. Find the area of shaded region.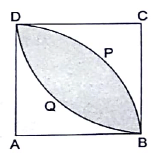
Given:
Side of square = 7 cm
Radius of each quadrant = 7 cm
Area of square = side × side = 7 × 7 = 49 cm2
∵ Area of quadrant = 1/4 πr2
∴ Area of 2 quadrants = 2 × 1/4 × πr2
=×
× 7 × 7
= 77 cm2
Area of shaded region = Area of 2 quadrants – Area of square
= 77 – 49 = 28 cm2
Hence, the area of shaded region is 28 cm2.
Q.34. In the given figure, OABC is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the shaded region.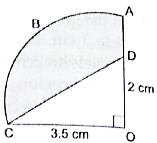
Given:
Radius of Circle = 3.5 cm
OD = 2 cm
∵ Area of Quadrant = 1/4 πr2
∴ Area of Quadrant OABC = 1/4 × 22/7 × 3.5 × 3.5
= 9.625 cm2
∵ Area of Triangle = 1/2 × Base × Height
∴ Area of Δ COD = 1/2 × 3.5 × 2
= 3.5 cm2
Area of Shaded Region = Area of Quadrant OABC – Area of ΔCOD
= 38.5 – 3.5 = 35 cm2
Hence, the area of shaded region is 35 cm2.
Q.35. Find the perimeter of shaded region in the figure, if ABCD is a square of side 14 cm and APB and CPD are semicircles.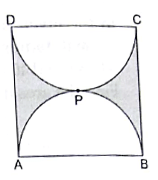
Given:
Side of square = 14 cm
Diameter of semi circle = 14 cm
⇒ Radius of semi circle = 14/2 = 7 cm
∵ There are 2 semi circles of same radius.
∴ We consider it as one circle with radius 7 cm.
So,
Perimeter of 2 semicircles = Perimeter of circle = 2πr
= 2 × (22/7) × 7
= 2 × 22 = 44 cm
Perimeter of shaded region = Perimeter of 2 semicircles + 2 × Side of Square = 44 + 2 × 14 = 44 + 28 = 72 cm
Hence, the area of the shaded region is 72 cm.
Q.36. In a circle of radius 7 cm, a square ABCD is inscribed. Find the area of the circle which is outside the square.
Given:
Radius of the circle = 7 cm
Diameter of the circle = 14 cm
Here, diagonal of square = 14 cm
∵ Side of a square =
⇒ Side = 14/√2 = 7√2 cm
⇒ Area of square = side × side
= 7√2 × 7√2
= 49 × 2 = 98 cm2
Area of circle = πr2
= 22/7 × 7 × 7 = 22 × 7 = 154 cm2
Thus, the area of the circle outside the square
= Area of circle – Area of square = 154 – 98 = 56 cm2
Hence, the area of the required region is 56 cm2.
Q.37. In the given figure, APB and CQD are semicircle of diameter 7 cm each, while ARC and BSD are semicircles of diameter 14 cm each. Find the (i) perimeter, (ii) area of the shaded region.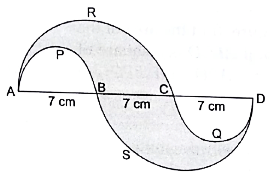
(i) Given:
Diameter of semicircles APB and CQD = 7 cm
⇒ Radius of semicircles APB and CQD = 7/2cm = r1
Diameter of semicircles ARC and BSD = 14 cm
⇒ Radius of semicircles ARC and BSD = 14/2 cm = 7 cm = r2
Perimeter of APB = Perimeter of CQD
Area of APB = Area of CQD ………….. (i)
Perimeter of ARC = Perimeter of BSD
Area of ARC = Area of BSD ………….. (ii)
∵ Perimeter of semicircle = πr …………… (iii)
∴ Perimeter of APB = πr1
=×
= 11 cm
Then, using (i), we have
Perimeter of CQD = 11 cm
Now, using (iii), we have
Perimeter of ARC = πr2
= (22/7) × 7 = 22 cm
Then, using (ii), we have
Perimeter of BSD = 22 cm
Perimeter of shaded region
= (Perimeter of ARC + Perimeter of APB) + (Perimeter of BSD + Perimeter of CQD)
= (22 + 11) + (22 + 11) = 33 + 33 = 66 cm
Hence, the perimeter of the shaded region is 66 cm.
(ii) Now,
∵ Area of semicircle = (1/2) πr2 …. (iv)
∴ Area of APB = (1/2) πr12
=×
×
×
=
cm2
Then, using (i), we have
Area of CQD = 77/4 cm2
Now, using (iv), we have
Area of ARC = 1/2 πr22
=×
× 7 × 7 = 11 × 7 = 77 cm2
Then, by using (ii), we have
Area of BSD = 77 cm2
Area of shaded region
= (Area of ARC-Area of APB) + (Area of BSD- Area of CQD)
= (77 -) + (77 -
)
= () + (
) =
+
=
= 115.5 cm2
Hence, the area of the shaded region is 115.5 cm2.
Q.38. In the given figure, PSR, RTQ and PAQ are three semicircles of diameter 10 cm, 3 cm and 7 cm respectively. Find the perimeter of shaded region.
Given:
Diameter of semicircle PSR = 10 cm
⇒ Radius of semicircle PSR = 10/2 = 5 cm = r1
Diameter of semicircle RTQ = 3 cm
⇒ Radius of semicircle RTQ = 3/2 = 1.5 cm = r2
Diameter of semicircle PAQ = 7 cm
⇒ Radius of semicircle PAQ = 7/2 = 3.5 cm = r3
∵ Perimeter of semicircle = πr
∴ Perimeter of semicircle PSR = πr1
= 3.14 × 5 = 15.7 cm
Similarly, Perimeter of semicircle RTQ = πr2
= 3.14 × 1.5 = 4.71 cm
and Perimeter of semicircle PAQ = πr3
= 3.14 × 3.5 = 10.99 cm
Perimeter of shaded region = Perimeter of semicircle PSR
+ Perimeter of semicircle RTQ
+ Perimeter of semicircle PAQ
= 15.7 + 4.71 + 10.99 = 31.4 cm
Hence, the perimeter of the shaded region is 31.4 cm.
Q.39. In the given figure, a square OABC is inscribed in a quadrant OPBQ of a circle. IF OA = 20 cm, find the area of the shaded region. [Use π = 3.14]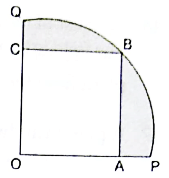
Given:
OA = Side of square OABC = 20 cm
∵ Area of square = Side × Side
∴ Area of square OABC = 20 × 20 = 400 cm2
Now,
∵ Length of diagonal of square = √2 × Side of Square
∴ Length of diagonal of square OABC = √2 × 20 = 20√2 cm
⇒ Radius of the quadrant = 20√2 cm
∵ Area of quadrant = 1/4πr2
∴ Area of quadrant OPBQ = (1/4) × 3.14 × 20√2 × 20√2
= 3.14/4 × 400 × 2
= 3.14 × 200 = 628 cm2
Area of shaded region = Area of quadrant OPBQ – Area of square OABC = 628 – 400 = 228 cm2
Hence, the area of the shaded region is 228 cm2.
Q.40. In the given figure, APB and AQO are semicircles and AO = OB. If the perimeter of the figure is 40 cm, find the area of the shaded region.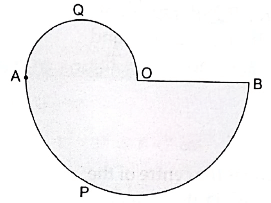
Given:
AO = OB
Perimeter of the figure = 40 cm………….. (i)
Let the diameters of semicircles AQO and APB be ‘x1’ and ‘x2’ respectively.
Then, using (1), we have
AO = OB
Also, AB = AO + OB = AO + AO = 2AO
⇒ x2 = 2x1
So, diameter of APB = 2x1
and diameter of AQO = x1
Radius of APB = x1
and Radius of AQO =x1/2 ….. (ii)
Perimeter of shaded region = perimeter of AQO + perimeter APB + diameter of APB …… (iii)
∵ Perimeter of semicircle = πr
∴ Perimeter of semicircle AQO =×
=
cm
Perimeter of semicircle APB =× x1 =
cm
Now, using (iii), we have
40 × 7 = 40x1
280 = 40x1
x1 = 280/40 = 7 cm∴ using (ii), we have
Radius of APB = 7 cm = r1
And Radius of AQO = 7/2 cm = 3.5 cm = r2
Now,
∵ Area of semicircle = 1/2 πr2
∴ Area of semicircle APB = 1/2 πr12
Similarly,
Area of semicircle APB = 1/2 πr22
Thus, Area of shaded region = Area of APB + Area of AQO
= 77 + 19.25 = 96.25 cm2
Hence, the area of the shaded region is 96.25 cm2.
Q.41. Find the area of a quadrant of a circle whose circumference is 44 cm.
Given:
Circumference of circle = 44 cm
Let the radius of the circle be ‘r’ cm
∵ Circumference of circle = 2πr
∴ 44 = 2πr=
× r
r = 22 × (7/22) = 7 cm
Now, Area of quadrant = 1/4 × πr2
Hence, the area of the quadrant is 38.5 cm2.
Q.42. In the given figure, find the area of the shaded region, where ABCD is a square of side 14 cm and all circles are of the same diameter.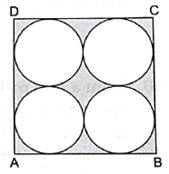
Given:
Side of square = 14 cm
Let the radius of each circle be ‘r’ cm
Then, 2r + 2r = 14 cm
4r = 14 cm
r = 14/4
= 7/2
Area of square = side × side
= 14 × 14
= 196 cm2
∵ Area of circle = πr2
∴ Area of 4 circles = 4 × πr2
= 22 × 7= 154 cm2
Area of shaded region = Area of the square – Area of 4 circles
= 196 -154
= 42 cm2
Hence, the area of the shaded region is 42 cm2.
Q.43. Find the area of the shaded region in the given figure, if ABCD is a rectangle wit sides 8 cm and 6 cm ad O is the centre of the circle.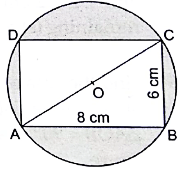
Given:
Length of rectangle = 8 cm
Breadth of rectangle = 6 cm
Area of rectangle = length × breadth
= 8 × 6 = 48 cm2
Consider Δ ABC,
By Pythagoras theorem,
AC2 = AB2 + BC2
= 82 + 62 = 64 + 36 = 100
AC = √100 = 10 cm
⇒ Diameter of circle = 10 cm
Thus, radius of circle = 10/2 = 5 cm
Let the radius of circle be r = 5 cm
Then, Area of circle = πr2
=× 5 × 5 =
=
= 78.57 cm2
Area of shaded region = Area of circle – Area of rectangle
= 78.57 - 48
= 30.57 cm2
Hence, the area of shaded region is 30.57 cm2.
Q.44. A wire is bent to form a square enclosing an area of 484 m2. Using the same wire, a circle is formed. Find the area of the circle.
Given:
Perimeter of square = Circumference of circle ……. (i)
Area of Square = 484m2
Let the side of square be ‘x’ cm.
∵ Area of Square = side × side
∴ 484 = x × x
x2 = 484
x = √484 = 22cm
∵ Perimeter of square = 4 × side
= 4 × 22 = 88 cm
∴ Using (i), we have
Circumference of circle = 88 cm
Also, Circumference of Circle = 2πr
2πr = 88
2 × 22/7 × r = 88
r = 2 × 7 = 14 cm
Area of Circle = πr2 = 22/7 × 14 × 14
= 22 × 2 × 14 = 616 cm2
Hence, the area of Circle is 616 cm2.
Q.45. A square ABCD is inscribed in a circle of radius ‘r’. Find the area of the square.
Given: Radius of circle = r
Diagonal of Square = 2r
∵ Side of Square =
∴ Side == √2r
Area of Square = Side × Side
= √2r × √2r
= 2r2
Hence, the area of square is ‘2r2’ square units.
Q.46. The cost of fencing a circular field at the rate of Rs. 25 per meter is Rs. 5500. The field is to be ploughed at the rate of 50 paise per m2. Find the cost of ploughing the field. [Take π = 22/7]
Given:
Rate of fencing a circular field = Rs. 25/m
Cost of fencing a circular field = Rs. 5500
Rate of ploughing the field = 50p/m2 = Rs. 0.5/m2
Let the radius of circular field be ‘r’ and the length of the field fenced be ‘x’ m.
Then, 25 × x = 5500
x = 5500/25 = 220 m
∵ Circumference of circular field = 2πr
∴ 220 = 2πr
220 = 2 × 22/7 × r
r =
r = 35 m
Area of the circular field = πr2
= 22/7 × 35 × 35
= 22 × 5 × 35
= 3850m2
Now, cost of ploughing the field = Rate of ploughing the field × Area of the field = 0.5 × 3850
= Rs. 1925
Hence, the cost of Ploughing the field is Rs. 1925.
Q.47. A park is in the form of a rectangle 120 m by 90 m. At the centre of the park, there is a circular lawn as shown in the figure. The area of the park excluding the lawn is 2950 m2. Find the radius of the circular lawn. [Given, π = 3.14]
Given:
Length of the rectangular park = 120 m
Breadth of the rectangular park = 90 m
Area of the park excluding the circular lawn = 2950m2
Area of the rectangular park = length × breadth
= 120 × 90 = 10800m2
Area of circular lawn = Area of rectangular park – Area of park excluding the lawn
= 10800 – 2950
= 7850m2
∵ Area of circle = πr2
∴ 7850 = 3.14 × r2
r2 = 7850/3.14 = 2500
r = √2500 = 50 m
Hence, the radius of the circular lawn is 50m.
Q.48. In the given figure PQSR represents a flower be. If OP = 21 m and OR = 14 m, find the area of the flower bed.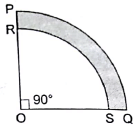
Given:
OP = 21 m = r1
OR = 14 m = r2
Let the quadrants made by outer and inner circles be Q1 and Q2, with radius r1 and r2 respectively.
Then, Area of flower bed = Area of Q1 – Area of Q2
∵ Area of Quadrant = 1/4 πr2
∴ Area of Q1 = 1/4 πr12
= 1/4 × 22/7 × 21 × 21= 693/2 m2
Similarly, Area of Q2 = 1/4 πr22
= 1/4 × 22/7 × 14 × 14
= 308/2 m2
Thus, Area of flower bed = 693/2 - 308/2
= 385/2 = 192.5 m2
Hence, the area of the flower bed is 192.5 m2.
Q.49. In the given figure, O is the centre of the bigger circle, and AC is its diameter. Another circle with AB as diameter is drawn. If AC = 54 cm and BC = 10 cm, find the area of the shaded region.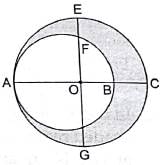
Given:
AC = 54 cm
BC = 10 cm
⇒ AB = AC-BC = 54-10 = 44 cm
Radius of bigger circle = AC/2 = 54/2 = 27 cm = r1
Radius of Smaller circle = AB/2 = 44/2 = 22 cm = r2
∵ Area of Circle = πr2
∴ Area of Bigger Circle = πr12
= (22/7) × 27 × 27
= 16038/7 cm2
Similarly, Area of Smaller Circle = πr22
= (22/7) × 22 × 22
= 10648/7 cm2
Area of shaded region = Area of Bigger Circle – Area of Smaller Circle = 16038/7 - 10648/7 = 5390/7 = 770 cm2
Hence, Area of Shaded Region is 770 cm2.
Q.50. From a thin metallic piece in the shape of a trapezium ABCD in which AB ∥ CD and ∠BCD = 90°, a quarter circle BFEC is removed. Given, AB = BC = 3.5 cm and DE = 2 cm, calculate the area of remaining (shaded) part of metal sheet.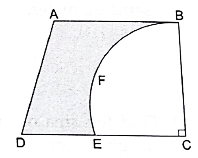
Given:
AB ∥ CD
∠BCD = 90°
AB = BC = 3.5 cm = EC
DE = 2 cm
DC = DE + EC = 2 + 3.5 = 5.5 cm
Area of Trapezium = 1/2 × Sum of Parallel Sides × h
= 1/2 × (AB + DC) × BC
= 1/2 × (3.5 + 5.5) × 3.5
= 1/2 × 9 × 3.5
= 15.75 cm2
Area of Quadrant BFEC = 1/4 × πr2 = 1/4 × 22/7 × 3.5 × 3.5
= 9.625 cm2
Thus, Area of remaining part of metal sheet
= Area of Trapezium – Area of Quadrant BFEC
= 15.75 – 9.625 = 6.125 cm2
Hence, the area of the remaining part of metal sheet is 6.125 cm2.
Q.51. Find the area of the major segment APB of a circle of radius 35 cm and ∠AOB = 90°, as shown in the given figure.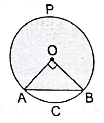
Given:
Radius of Circle = 35 cm
∠AOB = 90°
∵ Area of Sector =× πr2
=×
× 35 × 35
= 1925/2 cm2
∵ ∆ AOB is right-angled triangle.
∴ Area of ∆ AOB = 1/2 × OA × OB
= 1/2 × 35 × 35
= 1225/2 cm2
Now, Area of Minor Segment ACB
= Area of Sector – Area of ∆AOB
= 1925/2 - 1225/2 = 700/2 = 350 cm2
Area of Circle = πr2
= 22/7 × 35 × 35
= 22 × 5 × 35
= 3850 cm2
Thus, Area of Major Segment = Area of Circle – Area of Minor Segment = 3850 – 350 = 3500 cm2
Hence, the area of the major segment is 3500 cm2.