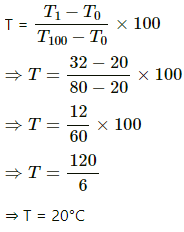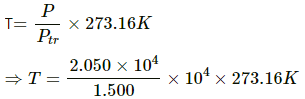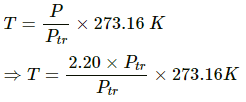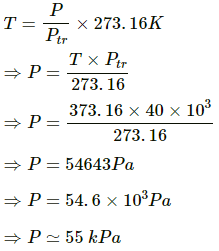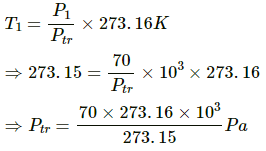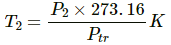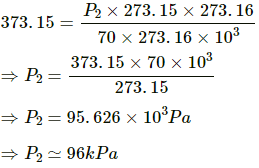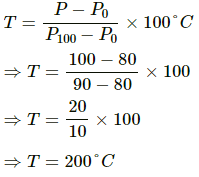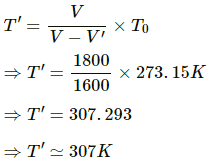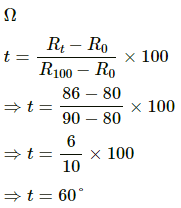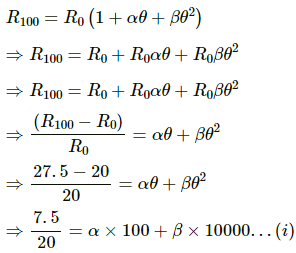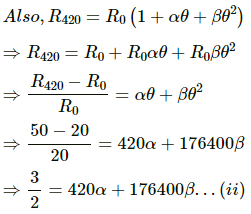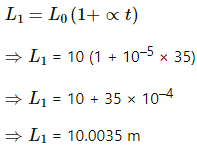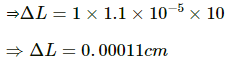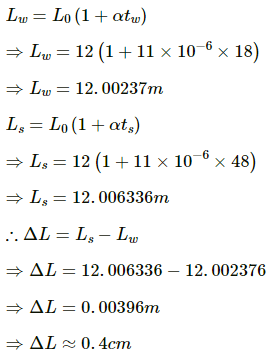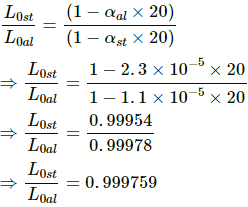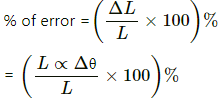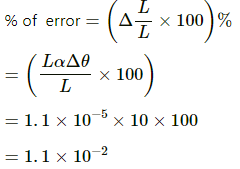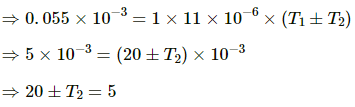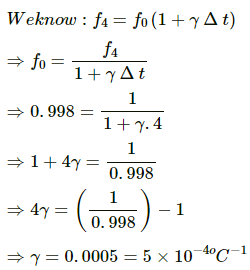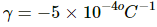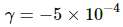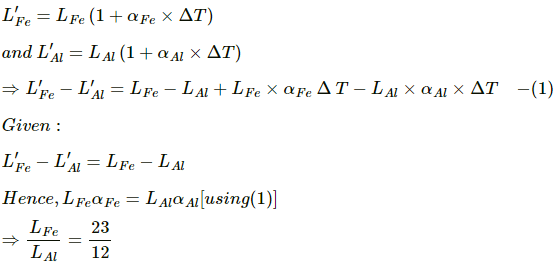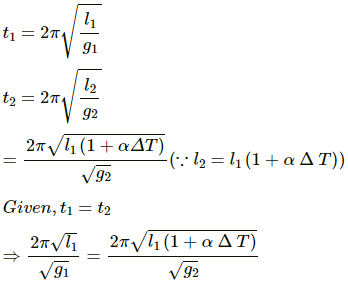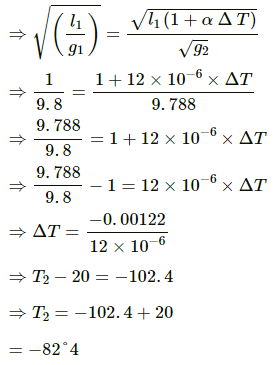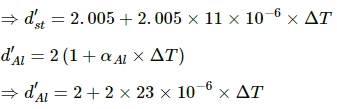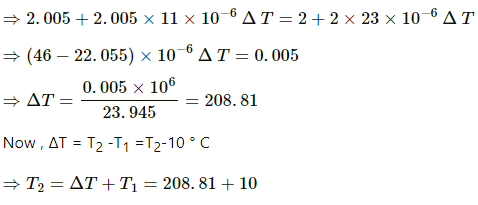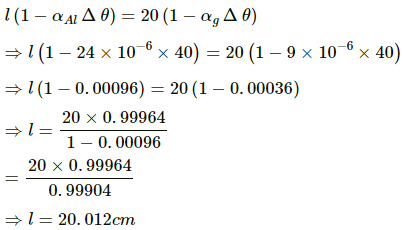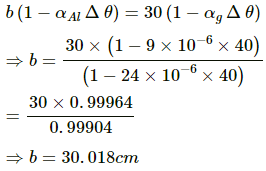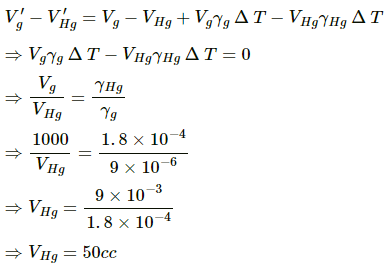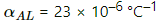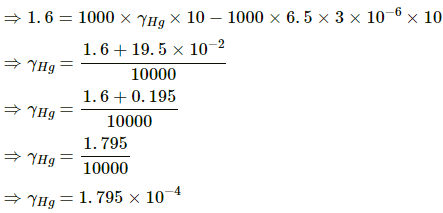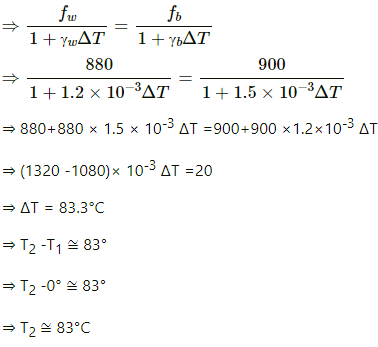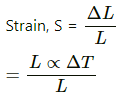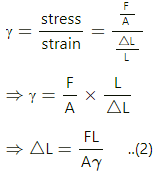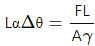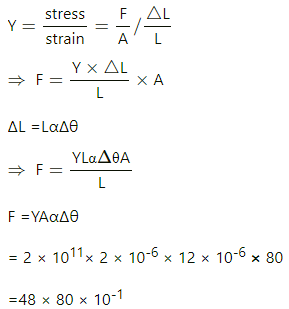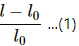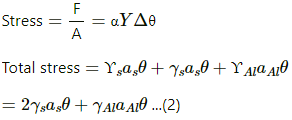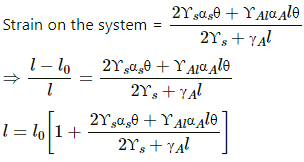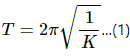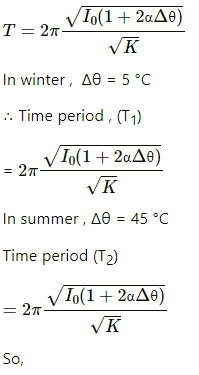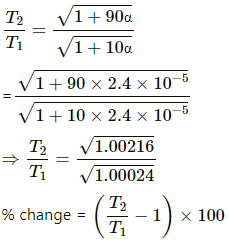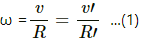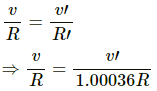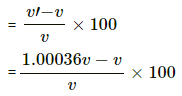HC Verma Questions and Solutions: Chapter 23: Heat and Temperature- 2 | HC Verma Solutions - JEE PDF Download

Q.1. The steam point and the ice point of a mercury thermometer are marked as 80° and 20°. What will be the temperature on a centigrade mercury scale when this thermometer reads 32°?

Given:
Ice point of a mercury thermometer, T0 = 20° C
Steam point of a mercury thermometer, T100 = 80° C
Temperature on thermometer that is to be calculated in centigrade scale, T1 = 32° C
Temperature on a centigrade mercury scale, T, is given as:

Therefore, the temperature on a centigrade mercury scale will be 20°C.

Q.2. A constant-volume thermometer registers a pressure of 1.500 × 10⁴ Pa at the triple point of water and a pressure of 2.050 × 10⁴ Pa at the normal boiling point. What is the temperature at the normal boiling point?

Given:
Pressure registered by a constant-volume thermometer at the triple point, P_tr = 1.500 × 10⁴  Pa
Pressure registered by the thermometer at the normal boiling point, P = 2.050 × 10⁴ Pa
We know that for a constant-volume gas thermometer, temperature (T) at the normal boiling point is given as:

⇒ T = 373.31 K
Therefore, the temperature at the normal point (T) is 373.31 K.

Q.3. A gas thermometer measures the temperature from the variation of pressure of a sample of gas. If the pressure measured at the melting point of lead is 2.20 times the pressure measured at the triple point of water, find the melting point of lead.

Given:
In a gas thermometer, the pressure measured at the melting point of lead, P = 2.20 × Pressure at triple point(P_tr)
So the melting point of lead, (T) is given as:

⇒ T =2.20 × 273.16 K
⇒  T = 600.952 K
⇒ T ≅  601 K
Therefore, the melting point of lead is 601 K.

Q.4. The pressure measured by a constant volume gas thermometer is 40 kPa at the triple point of water. What will be the pressure measured at the boiling point of water (100°C)?

Given:
Pressure measured by a constant volume gas thermometer at the triple point of water, P_tr = 40 kPa = 40 × 10³ Pa
Boiling point of water, T = 100°C = 373.16 K
Let the pressure measured at the boiling point of water be P.
For a constant volume gas thermometer, temperature-pressure relation is given below:

Therefore, the pressure measured at the boiling point of water is 55 kPa.

Q.5. The pressure of the gas in a constant volume gas thermometer is 70 kPa at the ice point.  Find the pressure at the steam point.

Given:
Temperature of ice point, T₁ = 273.15 K
Temperature of steam point, T₂ = 373.15 K
Pressure of the gas in a constant volume thermometer at the ice point, P₁ = 70 kPa,        
Let Ptr be the pressure at the triple point and P₂ be the pressure at the steam point.
The temperature-pressure relations for ice point and steam point are given below:
For ice point,

For steam point,

On substituting the value of P_tr, we get:

Therefore, the pressure at steam point is 96 kPa.

Q.6. The pressures of the gas in a constant volume gas thermometer are 80 cm, 90 cm and 100 cm of mercury at the ice point, the steam point and in a heated wax bath, respectively. Find the temperature of the wax bath.

Given:
In a constant volume gas thermometer,
Pressure of the gas at the ice point, P₀ = 80 cm of Hg
Pressure of the gas at the steam point, P₁₀₀ = 90 cm of Hg
Pressure of the gas in a heated wax bath, P = 100 cm of Hg
The temperature of the wax bath
(T) is given by:

Therefore, the temperature of the wax bath is 200°C.

Q.7. In a Callender's compensated  constant pressure air thermometer, the volume of the bulb is 1800 cc. When the bulb is kept immersed in a vessel, 200 cc of mercury has to be poured out. Calculate the temperature of the vessel.

Given:
Volume of the bulb in a Callender's compensated constant pressure air thermometer, (V) = 1800 cc
Volume of mercury that has to be poured out, V' = 200 cc
Temperature of ice bath, To = 273.15 K
So the temperature of the vessel(T') is given by:

Therefore, the temperature of the vessel is 307 K.

Q.8. A platinum resistance thermometer reads 0° when its resistance is 80 Ω and 100° when its resistance is 90 Ω. Find the temperature at the platinum scale at which the resistance is 86 Ω.

Given:
Resistance at 0oC, R0 = 80Ω
Resistance at 100oC, R100 = 90Ω
Let t be the temperature at which the resistance (Rt) is 86

Therefore, the resistance is 86Ω at 60°C.

Q.9. A resistance thermometer reads R = 20.0 Ω, 27.5 Ω, and 50.0 Ω at the ice point (0°C), the steam point (100°C) and the zinc point (420°C), respectively. Assuming that the resistance varies with temperature as R_θ = R₀ (1 + αθ + βθ²), find the values of R₀, α and β. Here θ represents the temperature on the Celsius scale.

Given:
Reading on resistance thermometer at ice point, R₀ = 20 Ω
Reading on resistance thermometer at steam point, R₁₀₀ = 27.5 Ω
Reading on resistance thermometer at zinc point, R₄₂₀ = 50 Ω
The variation of resistance with temperature in Celsius scale,θ, is given as:


Solving (i) and (ii), we get:
α = 3.8 ×10^–3°C^-1
β = –5.6 ×10^–7°C^-1
Therefore, resistance R₀ is 20 Ω and the value of α is 3.8 ×10^–3°C^-1  and that of β is –5.6 ×10^–7°C^-1.

Q.10. A concrete slab has a length of 10 m on a winter night when the temperature is 0°C. Find the length of the slab on a summer day when the temperature is 35­°C. The coefficient of linear expansion of concrete is 1.0 × 10^–5 °C^–1.

Given:
Length of the slab when the temperature is 0°C,  L₀ = 10 m
Temperature on the summer day, t = 35­ °C
Let L₁ be the length of the slab on a summer day when the temperature is 35°C.
The coefficient of linear expansion of concrete, α = 1 ×10^–5 °C^-1

So, the length of the slab on summer day when the temperature is 35°C is 10.0035 m.

Q.11. A metre scale made of steel is calibrated at 20°C to give correct reading. Find the distance between the 50 cm mark and the 51 cm mark if the scale is used at 10°C. Coefficient of linear expansion of steel is 1.1 × 10^–5 °C^–1.

Given:
Temperature at which the steel metre scale is calibrated, t₁ = 20°C
Temperature at which the scale is used, t₂ = 10°C
So, the change in temperature,
Δt = 20°−10°) C
The distance to be measured by the metre scale, L_o = 51-50) = 1 cm = 0.01 m
Coefficient of linear expansion of steel,
α_steel= 1.1 × 10^–5 °C^–1
Let the new length measured by the scale due to expansion of steel be L₂, Change in length is given by,
ΔL = L₁ ∝_steel Δt

As the temperature is decreasing, therefore length will decrease by ΔL
Therefore, the new length measured by the scale due to expansion of steel (L₂) will be, L₂ = 1 cm
− 0.00011 cm = 0.99989 cm

Q.12. A railway track (made of iron) is laid in winter when the average temperature is 18°C. The track consists of sections of 12.0 m placed one after the other. How much gap should be left between two such sections, so that there is no compression during summer when the maximum temperature rises to 48°C? Coefficient of linear expansion of iron = 11 × 10^–6 °C^–1.

Given:
Length of the iron sections when there's no effect of temperature on them, L_o  = 12.0 m
Temperature at which the iron track is laid in winter, t_w = 18°C
Maximum temperature during summers, t_s = 48°C
Coefficient of linear expansion of iron,
α = 11 × 10^–6  °C^–1
Let the new lengths attained by each section due to expansion of iron in winter and summer be L_w and L_s, respectively, which can be calculated as follows:

Therefore, the gap (ΔL) that should be left between two iron sections, so that there is no compression during summer, is 0.4 cm.

Q.13. A circular hole of diameter 2.00 cm is made in an aluminium plate at 0°C. What will be the diameter at 100°C? α for aluminium = 2.3 ×  10^–5 °C^–1.

Given:
Diameter of a circular hole in an aluminium plate at 0°C, d₁ = 2 cm = 2 × 10^–2 m        
Initial temperature, t₁ = 0 °C
Final temperature, t₂ = 100 °C
So, the change in temperature, (Δt) = 100°C - 0°C = 100°C
The linear expansion coefficient of aluminium, αal = 2.3 × 10^–5 °C^–1 
Let the diameter of the circular hole in the plate at 100°C be d₂ , which can be written as
d₂ = d₁(1+αΔt)
⇒ d₂ =2 × 10^-2(1+2.3×10^-5×10²)
⇒ d₂ = 2×10^-2(1+2.3×10^-3)
⇒ d₂ = 2×10^-2+2.3×2×10^-5
⇒ d₂ = 0.02 +0.000046
⇒ d² =0.020046 m
⇒ d² ≈ 2.0046 cm
Therefore, the diameter of the circular hole in the aluminium plate at 100°C is 2.0046 cm.

Q.14. Two metre scales, one of steel and the other of aluminium, agree at 20°C. Calculate the ratio aluminium-centimetre/steel-centimetre at (a) 0°C, (b) 40°C and (c) 100°C. α for steel = 1.1 × 10^–5 °C^–1 and for aluminium = 2.3 × 10^–5°C^–1.

Given:
At 20°C, length of the metre scale made up of steel, Lst= length of the metre scale made up of aluminium, L_al
Coefficient of linear expansion for aluminium, α_al = 2.3 × 10^–5 °C^-1
Coefficient of linear expansion for steel, α_st = 1.1 × 10^–5 °C^-1
Let the length of the aluminium scale at 0°C, 40°C and 100°C be L0al, L_40al and L_100al.
And let the length of the steel scale at 0°C, 40°C and 100°C be L_0st, L_40st and L_100st.
(a) So, L_0st(1 – α_st × 20) = L_0al(1 – α_al × 20)

Q.15. A metre scale is made up of steel and measures correct length at 16°C. What will be the percentage error if this scale is used (a) on a summer day when the temperature is 46°C and (b) on a winter day when the temperature is 6°C? Coefficient of linear expansion of steel = 11 × 10^–6 °C^–1.

(a) Let the correct length measured by a metre scale made up of steel 16 °C be L.
Initial temperature, t₁ = 16 °C      
Temperature on a hot summer day, t₂ = 46 °C
So, change in temperature, Δθ = t₂
−t₁  = 30 °C
Coefficient of linear expansion of steel,
α = 1.1 × 10^–5 °C^-1
Therefore, change in length,
ΔL = L αΔθ = L × 1.1 × 10^–5 × 30

=[1.1 × 10^-5 × 30 ×100]%
=3.3 × 10^-2 %
(b) Temperature on a winter day, t₂ = 6 °C
So, change in temperature, Δθ = t₁
−t₂ = 10 °C
ΔL = L₂
− L₁ = L αΔθ = L × 1.1 × 10^–5 × 10

Q.16. A metre scale made of steel reads accurately at 20°C. In a sensitive experiment, distances accurate up to 0.055 mm in 1 m are required. Find the range of temperature in which the experiment can be performed with this metre scale. Coefficient of linear expansion of steel  = 11 × 10^–6 °C^–1.

Given:
Temperature at which a metre scale gives an accurate reading, T₁ = 20 °C
The value of variation admissible, ΔL = 0.055 mm = 0.055 × 10^–3 m, in the length, L₀ = 1 m
Coefficient of linear expansion of steel, α  = 11 × 10^–6  °C^–1
Let the range of temperature in which the experiment can be performed be T₂.
We know:  ΔL = L₀ αΔT

Either T₂ = 20 + 5 = 25°C
or T₂= 20 - 5 = 15°C
Hence, the experiment can be performed in the temperature range of 15 °C.

Q.17. The density of water at 0°C is 0.998 g cm^–3 and at 4°C is 1.000 g cm^–1. Calculate the average coefficient of volume expansion of water in the temperature range of 0 to 4°C.

Given:
Density of water at 0°C, ( f₀)= 0.998 g cm^-3
Density of water at 4°C,  (f₄) = 1.000 g cm^-3
Change in temperature, (Δt) = 4°C
Let the average coefficient of volume expansion of water in the temperature range of 0 to 4°C be γ.

As the density decreases,

Therefore, the average coefficient of volume expansion of water in the temperature range of 0 to 4°C will be

Q.18. Find the ratio of the lengths of an iron rod  and an aluminium rod for which the difference in the lengths is independent of temperature. Coefficients of linear expansion of iron and aluminium are 12 × 10^–6 °C^–1 and 23 × 10^–6 °C^–1 respectively.

Let the original length of iron rod be LFe and L'Fe be its length when temperature is increased by ΔT.
Let the original length of aluminium rod be LAl and L'Al be its length when temperature is increased by ΔT.
Coefficient of linear expansion of iron,
...(1)
Coefficient of linear expansion of aluminium, α_Al = 23 × 10^–6 °C ...(1)
Since the difference in length is independent of temperature, the difference is always constant.

The ratio of the lengths of the iron to the aluminium rod is 23:12.

Q.19. A pendulum clock shows correct time at 20°C at a place where g = 9.800 m s^–2. The pendulum consists of a light steel rod connected to a heavy ball. It is taken to a different place where g = 9.788 m s^–1. At what temperature will the clock show correct time? Coefficient of linear expansion of steel = 12 × 10^–6 °C^–1.

Given:
The temperature at which the pendulum shows the correct time, T₁ = 20 °C
Coefficient of linear expansion of steel, 

α = 12 × 10^–6 °C^–1
Let T₂ be the temperature at which the value of g is 9.788 ms^–2 and
ΔT be  the change in temperature.
So, the time periods of pendulum at different values of g will be t₁ and t₂ , such that


⇒ T₂ ≈ -82° C
Therefore, for a pendulum clock to give correct time, the temperature at which the value of g is 9.788 ms^–2 should be −82°C.

Q.20. An aluminium plate fixed in a horizontal position has a hole of diameter 2.000 cm. A steel sphere of diameter 2.005 cm rests on this hole. All the lengths refer to a temperature of 10 °C. The temperature of the entire system is slowly increased. At what temperature will the ball fall down? Coefficient of linear expansion of aluminium is 23 × 10^–6 °C^–1 and that of steel is 11 × 10^–6 °C^–1.

Given:
Diameter of the steel sphere at temperature (T1 = 10 °C) , dst = 2.005 cm
Diameter of the aluminium sphere, dAl = 2.000 cm
Coefficient of linear expansion of steel, αst  = 11 × 10
-6°C
-1
Coefficient of linear expansion of aluminium, α_Al  = 23 × 10
−6 °C
-1
Let the temperature at which the ball will fall be T₂ , so that change in temperature be ΔT.
d'_st = 2.005(1 + α_st ΔT)

The steel ball will fall when both the diameters become equal.
So, d'_st = d'_Al

⇒ T₂ = 218.8 ≅ 219°C
Therefore, the temperature at which the ball will fall is 219 °C.

Q.21. A glass window is to be fit in an aluminium frame. The temperature on the working day is 40°C and the glass window measures exactly 20 cm × 30 cm. What should be the size of the aluminium frame so that there is no stress on the glass in winter even if the temperature drops to 0°C? Coefficients of linear  expansion for glass  and aluminium are 9.0 × 10^–6 °C^–1 and 24 ×100^–6°C^–1 , respectively.

Given:
At 40oC, the length and breadth of the glass window are 20 cm and 30 cm, respectively.
Coefficient of linear expansion of glass,
α_g =  9.0 × 10^–6 °C^–1
Coefficient of linear expansion for aluminium,

α_Al = 24 ×100^–6 °C^–1
The final length of aluminium should be equal to the final length of glass so that there is no stress on the glass in winter, even if the temperature drops to 0 °C.
Change in temperature,
Δθ  = 40 °C
Let the initial length of aluminium be l.

Let the initial breadth of aluminium be b.

Therefore, the size of the aluminium frame should be 20.012 cm × 30.018 cm.

Q.22. The volume of a glass vessel is 1000 cc at 20°C. What volume of mercury should be poured into it at this temperature so that the volume of the remaining space does not change with temperature? Coefficients of cubical expansion of mercury and glass are 1.8 × 10^–6 °C^–1 and 9.0 × 10^–6 °C^–1 , respectively.

At T = 20°C, the volume of the glass vessel,  V_g = 1000 cc.
Let the volume of  mercury be V_Hg .
Coefficient of cubical expansion of mercury, γ_Hg = 1.8 × 10^–4 /°C
Coefficient of cubical expansion of glass, γ_g = 9 × 10^–6 /°C
Change in temperature, ΔT, is same for glass and mercury.
Let the volume of glass and mercury after rise in temperature be V'_g and V'_Hg respectively.
Volume of remaining space after change in temperature,(V'_g – V'_Hg) = Volume of the remaining space (initial),(V_g – V_Hg)
We know:  V'_g = V_g (1 + γ_g ΔT)  ...(1)
V'_Hg = V_Hg (1 + γ_Hg ΔT)  ...(2)
Subtracting (2) from (1), we get:

Therefore, the volume of mercury that should be poured into the glass vessel is 50 cc.

Q.23. An aluminium can of cylindrical shape contains 500 cm³ of water. The area of the inner cross section of the can is 125 cm². All measurements refer to 10°C.
Find the rise in the water level if the temperature increases to 80°C. The coefficient of linear expansion of aluminium is 23 × 10^–6 °C^–1 and the average coefficient of the volume expansion of water is 3.2 × 10^–4 °C^–1.

Given:
Volume of water contained in the aluminium can, V₀ = 500 cm³
Area of inner cross-section of the can, A = 125 cm²
Coefficient of volume expansion of water, γ = 3.2 × 10^–4 °C^–1 
Coefficient of linear expansion of aluminium,

If  ∆θ  is the change in temperature, then final volume of water (V) due to expansion,
V = V₀(1 + γΔθ)
= 500 [1 + 3.2 × 10^–4 × (80 – 10)]
= 500 [1 + 3.2 × 10^–4 × 70]
= 511.2 cm³
The aluminium vessel expands in its length only.
So, area of expansion of the base can be neglected.
Increase in volume of water = 11.2 cm³ 
Consider a cylinder of volume 11.2 cm³
∴ Increase in height of the water
=11.2/125 = 0.0896
= 0.089 cm

Q.24. A glass vessel measures exactly 10 cm × 10 cm × 10 cm at 0°C. It is filled completely with mercury at this temperature. When the temperature is raised to 10°C, 1.6 cm³ of mercury overflows. Calculate the coefficient of volume expansion of mercury. Coefficient of linear expansion of glass = 6.5 × 10^–1 °C^–1.

Given: At 0°C, volume of glass vessel, V_g = 10 × 10 × 10 = 1000 cc = volume of mercury, V_Hg
Let the volume of mercury at 10°C be V'_Hg and that of glass be V'_g.
At 10°C, the additional volume of mercury than glass, due to heating, V'_Hg – V'_g = 1.6 cm³
So change in temperature, ΔT = 10°C
Coefficient of linear expansion of glass, α_g = 6.5 × 10^–6 °C^–1
Therefore, the coefficient of volume expansion of glass, γ_g = 3 × 6.5 × 10^–6°C^–1 
 Let the coefficient of volume expansion of mercury be γHg.
 We know that
V'_Hg = V_Hg (1 + γ_Hg ΔT)         ...(1)
V'_g = V_g (1 + γ_g ΔT)              ...(2)
Subtracting (2) from (1) we get,
V'_Hg – V'_g = V_Hg – V_g + V_Hg γ_Hg ΔT – V_g γ_g ΔT (as V_Hg = V_g)

⇒ γ_Hg ≅ 1.8 × 10^-4°C^-1
Therefore, the coefficient of volume expansion of mercury is 1.8× 10^–4 °C^–1.

Q.25. The densities of wood  and benzene at 0°C are 880 kg m³ and 900 kg m^–3 , respectively. The coefficients of volume expansion are 1.2 × 10^–3°C^–1 for wood and 1.5 × 10^–3°C^–1 for benzene. At what temperature will a piece of wood just sink in benzene?

Given:
Density of wood at 0 °C, f_w = 880 kgm^-3
Density of benzene at 0 °C, f_b = 900 kgm^-3
Coefficient of volume expansion for wood, γ_w = Coefficient of volume expansion for benzene, γ_b = 1.5 × 10^–3 °C^–1
So, initial temperature, T₁ = 0 °C
Let T2 be the temperature at which the piece of wood will just sink in benzene and ΔT = T₂-T₁.
The piece of wood begins to sink when its weight is equal to the weight of the benzene displaced.
Mass = volume × density
Therefore, Vf_wg = Vf_bg

Therefore, the piece of wood will just sink in benzene at 83 °C.

Q.26. A steel rod of length 1 m rests on a smooth horizontal base. If it is heated from 0°C to 100°C, what is the longitudinal strain developed?

The steel rod is resting on a horizontal base at 0 °C. When the temperature is increased to 100 °C, it will lead to an increase in the length of the steel due to expansion on heating. Since, there is no opposition in expansion of length, no longitudinal strain will be developed.

Q.27. A steel rod is clamped at its two ends and rests on a fixed horizontal base. The rod is unstrained at 20°C.
Find the longitudinal strain developed in the rod if the temperature rises to 50°C. Coefficient of linear expansion of steel = 1.2 × 10^–5 °C^–1.

Given:
Temperature at which rod is resting on a fixed horizontal base without any strain, T₁=20 °C. Then the rod is heated to temperature, T₂ = 50 °C
So change in temperature,ΔT =T₂-T₁=30°C
Coefficient of linear expansion of steel, α = 1.2 × 10^–5 °C^-1 
Let L be the length of the rod without heating and L' be the length of the rod on heating.
Let longitudinal strain developed in the rod be S.
We know that
L' =L(1+∝ΔT)
⇒ ΔL =L∝ΔT

=αΔT
⇒ S =1.2 × 10^-5 ×(50-20)
=1.2 × 10^-5 ×30
=1.2 × 10^-5 × 30
=36 × 10^-5 
S = 3.6 × 10^-4
The strain of 3.6 × 10^-4 will be opposite to the direction of expansion.

Q.28. A steel wire of cross-sectional area 0.5 mm² is held between two fixed supports. If the wire is just taut at 20°C, determine the tension when the temperature falls to 0°C. Coefficient of linear expansion of steel is 1.2 × 10^–5 °C^–1 and its Young's modulus is 2.0 × 10^–11 Nm^–2.

Given:
Cross-sectional area of the steel wire, A = 0.5 mm² = 0.5 × 10^–6 m²
The wire is taut at a temperature, T₁ = 20 °C,
After this, the temperature is reduced to T₂ = 0 °C
So, the change in temperature, Δθ = T₁-T₂ = 20 °C
Coefficient of linear expansion of steel, α = 1.2 ×10^–5 °C^-1
Young's modulus, γ = 2 ×10¹¹ Nm^-2
Let L be the initial length of the steel wire and L' be the length of the steel wire when temperature is reduced to 0°C.
Decrease in length due to compression, ΔL =L' - L = LαΔθ ...(1)
Let the tension applied be F.

Change in length due to tension produced is given by (1) and (2).
So, on equating (1) and (2), we get:

⇒ F = αΔθAγ
= 1.2 × 10^-5 × (20-0) × 0.5 ×10^-6 × 2 ×10¹¹
= 1.2 × 20
⇒ F = 24 N
Therefore, the tension produced when the temperature falls to 0°C.

Q.29. A steel rod is rigidly clamped at its two ends. The rod is under zero tension at 20°C. If the temperature rises to 100°C, what force will the rod exert on one of the clamps? Area of cross-section of the rod is 2.00 mm². Coefficient of linear expansion of steel is 12.0 × 10^–6 °C^–1 and Young's modulus of steel is 2.00 × 10¹¹ Nm^–2.

Given:
Temperature of the rod at zero tension, T₁ = 20 °C
Final temperature, T₂ = 100 °C
Change in temperature, Δθ =80°C
Cross-sectional area of the rod, A = 2 mm² = 2 × 10^-6m²
Coefficient of linear expansion of steel, α = 12 ×10^–6 °C^-1
Young's modulus of steel, Y = 2 × 10¹¹ Nm^-2
Let L be the length of the steel rod at 20 °C and L' be the length of steel rod at 100 °C.
Change of length of the rod, ΔL =L' - L
If F be the force exerted by the rod on one of the clamps due to rise in temperature, then

So, F = 384 N
Therefore, the rod will exert a force of 384 N on one of the clamps.

Q.30. Two steel rods and an aluminium rod of equal length l0 and equal cross-section are joined rigidly at their ends, as shown in the figure below. All the rods are in a state of zero tension at 0°C. Find the length of the system when the temperature is raised to θ. Coefficient of linear expansion of aluminium and steel are α_a and α_s, respectively. Young's modulus of aluminium is Y_a and of steel is Y_s.

Given:-
Initial length of the system (two identical steel rods + an aluminium rod) at 0 °C = l₀
Coefficient of linear expansion of steel and aluminium are α_s and α_Al, respectively.
Temperature is raised by θ.
So, the change in temperature, Δθ = θ - 0 ° C = θ
Young's modulus of steel and aluminium are γ_s and γ_Al, respectively.
If l be the final length of the system at temperature θ, strain on the system =
Young's modulus = Stress/Strain
Therefore, the total strain on the system = Total stress on the system/Total Young's modulus of the system
Now, total stress = stress due to the two steel rods + stress due to  the aluminium rod

Young's modulus of the system,
Y = ϒ_s +ϒ_s+ϒ_Al = 2ϒ_s + ϒ_Al  ...(3)
Using (1), (2) and (3), we get:

Therefore, the final length of the system will be l₀ where l₀ is its  initial length.

Q.31. A steel ball that is initially at a pressure of 1.0 × 10⁵ Pa is heated from 20°C to 120°C, keeping its volume constant.
Find the pressure inside the ball. Coefficient of linear expansion of steel = 12 × 10^–6 °C^–1 and bulk modulus of steel = 1.6 × 10¹¹ Nm^–2.

Given:
Initial pressure on the steel ball = 1.0 × 10⁵ Pa
The ball is heated from 20 °C to 120 °C.
So, change in temperature, Δθ = 100°C.
Coefficient of linear expansion of steel, α = 12 ×10^-6°C^-1
Bulk modulus of steel ,B = 1.6 × 10¹¹ Nm^–2
Pressure is given as,
⇒ P = B × γ Δθ
⇒ P =B × 3 αΔθ  (∵ γ = 3 α )
⇒ P = 1.6 × 10¹¹ ×3 × 12 × 10^-6 ×(120-20)
=1.6 ×  3 × 12 ×10¹¹ ×10^-6 ×10²
= 57.6 × 10⁷ 
⇒ P =5.8 × 10⁸ Pa
Therefore, the pressure inside the ball is 5.8 × 10⁸ Pa.

Q.32. Show that the moment of inertia of a solid body of any shape changes with temperature as I = I₀ (1 + 2αθ), where I₀ is the moment of inertia at 0°C and α is the coefficient of linear expansion of the solid.

Given:

Coefficient of linear expansion of solid = α 

Moment of inertia at 0 °C = I₀

If temperature changes to θ from 0 °C, then change in temperature, (ΔT) =θ

Let I be the new moment of inertia attained due to rise in temperature.

Let R₀ be the radius of gyration at 0 °C.

We know that on heating, radius of gyration will change as

 R = R₀(1 + αθ)

Here, R is the radius of gyration after heating.

 I0 = MR₀² , where M = mass of the body

Now, I = MR² = MR₀²(1 + αθ)² 

Expanding binomially and neglecting the higher terms of order (αθ) that will be very small, we get

I = MR₀²(1 + 2 αθ)

So, I = I₀(1 + 2 αθ)

Hence, proved.

Q.33. A torsional pendulum consists of a solid  disc connected to a thin wire (α = 2.4 × 10^–5°C^–1) at its centre. Find the percentage change in the time period between peak winter (5°C) and peak summer (45°C).

Given:
Coefficient of linear expansion of the wire, α = 2.4 × 10^–5 °C^–1
Let I₀ be the moment of inertia of the torsional pendulum at 0 °C.
If K is the torsional constant of the wire, then time period of torsional pendulum (T):

Here, I = moment of inertia after change in temperature
When the temperature is changed by Δθ, moment of inertia (I),
l = l₀(1+2αΔθ)
On substituting the value of I  in equation(1), we get:


= 0.0959 %
⇒ % change in time period ≈ 9.6 ×  10^-2 %
Therefore, the percentage change in time period of a torsional pendulum between peak winters and peak summers is 9.6 × 10^–2 %.

Q.34. A circular disc made of iron is rotated about its axis at a constant velocity ω. Calculate the percentage change in the linear speed of a particle of the rim as the disc is slowly heated from 20°C to 50°C, keeping the angular velocity constant. Coefficient of linear expansion of iron = 1.2 × 10^–5 °C^–1.

Let initial radius of the circular disc at 20 °C = r₂₀
Let final radius of the circular disc at 50°C = r₅₀
Coefficient of linear expansion of iron, α = 1.2 × 10^–5 °C^–1.
change in temperature,ΔT = 30°C
Let R' and R be the radius of the paricle at 50°C and 20°C respectively.
If v and v' be the linear speed of the particle at 50 °C and 20 °C respectively, as the angular velocity remains (ω) constant.
Therefore,

Now,
R' = R (1+αΔT)
⇒ R' =R +R × 1.2 ×10^-5 ° C^-1 × Δ T
⇒ R' = 1.00036R
Using equation(1) we have,

⇒ v' = 1.00036v
Percentage change in linear speed will be,

= 3.6 × 10^-2