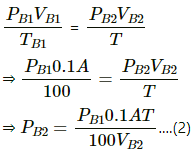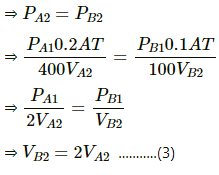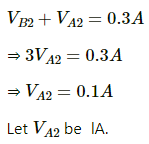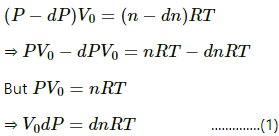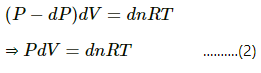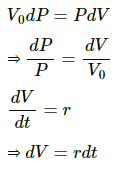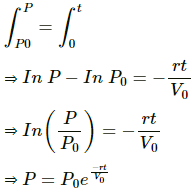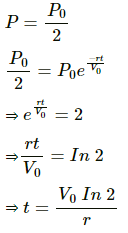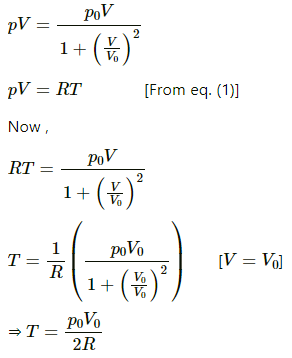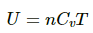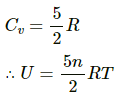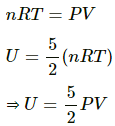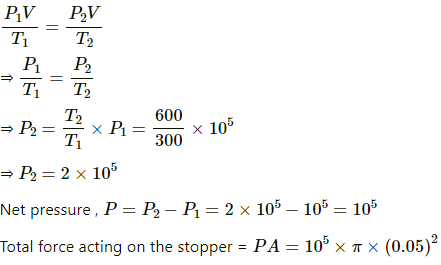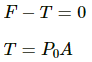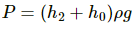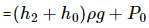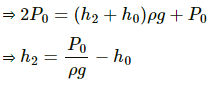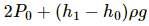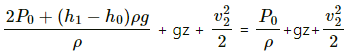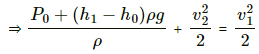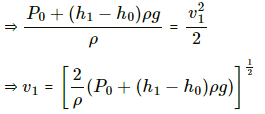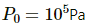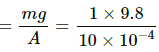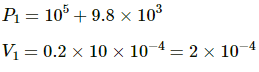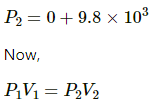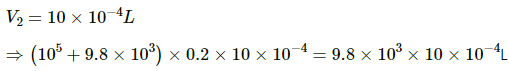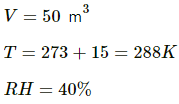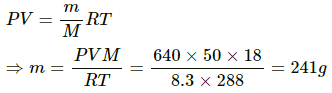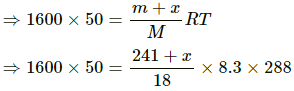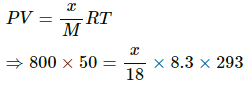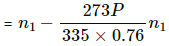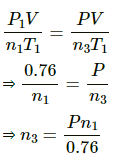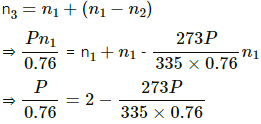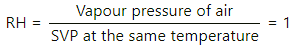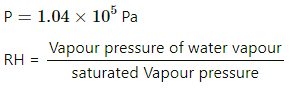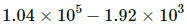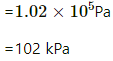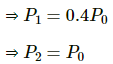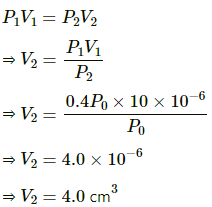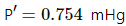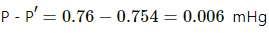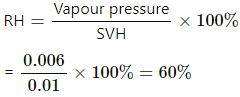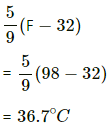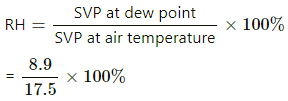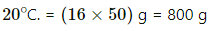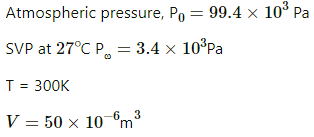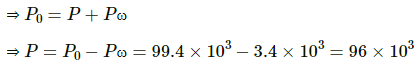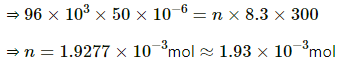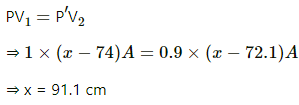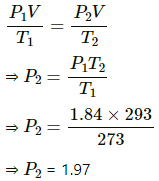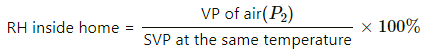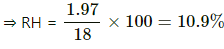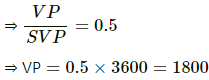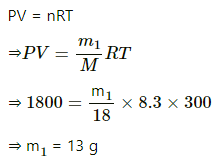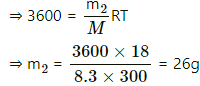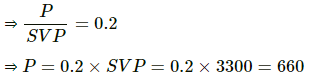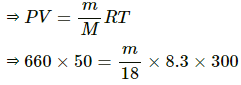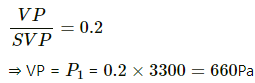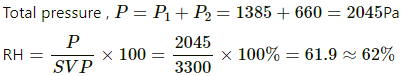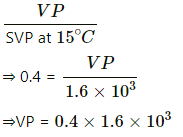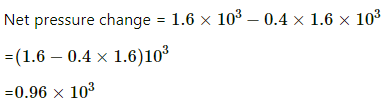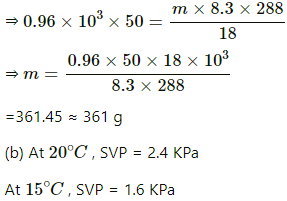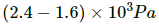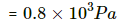HC Verma Questions and Solutions: Chapter 24: Kinetic Theory of Gases- 3 | HC Verma Solutions - JEE PDF Download
Q.36. Figure shows a cylindrical tube of length 30 cm which is partitioned by a tight-fitting separator. The separator is very weakly conducting and can freely slide along the tube. Ideal gases are filled in the two parts of the vessel. In the beginning, the temperatures in the parts A and B are 400 K and 100 K respectively. The separator slides to a momentary equilibrium position shown in the figure. Find the final equilibrium position of the separator, reached after a long time.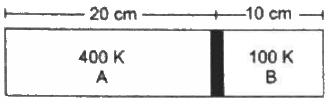
Let the initial pressure of the chambers A and B be PA1 and PB1 , respectively .
Let the final pressure of chambers A and B be PA2 and PB2 , respectively .
Let the CSA be A.
VA1 = 0.20 A
TA1 = 400 K
VB1 = 0.1 A
TB1 = 100 K
At first equilibrium , both side pressures will be the same .
⇒ PA1 = PB1
Let the final temperature at equilibrium be T .then ,
For Second chamber :
At Second equilibrium , pressures on both sides will be the same .
Now ,
⇒ l = 0.1 m
⇒ l = 10 cm
Q.37. A vessel of volume V0 contains an ideal gas at pressure p0 and temperature T. Gas is continuously pumped out of this vessel at a constant volume-rate dV/dt = r keeping the temperature constant. The pressure of the gas being taken out equals the pressure inside the vessel. Find (a) the pressure of the gas as a function of time, (b) the time taken before half the original gas is pumped out.
Use R = 8.3 J K-1 mol-1.
Let P be the pressure and n be the number of moles of gas inside the vessel at any given time t .
Suppose a small amount of gas of dn moles is pumped out and the decrease in pressure is dP .
Applying equation of state to the gas inside the vessel , we get
The pressure of the gas taken out is equal to the inner pressure .
Applying equation of state , we get
From eq. (1) and eq. (2) , we get........(3) [Since pressures decreases , rate is negative]
Now,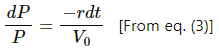
(a) Integrating the equation P = P0 to P = P and time t = 0 to t = t , we get
(b)
Q.38. One mole of an ideal gas undergoes a process 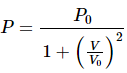 where p0 and V0 are constants. Find the temperature of the gas when V = V0.
where p0 and V0 are constants. Find the temperature of the gas when V = V0.
Given :
Multiplying both sides by V, we get
Q.39. Show that the internal energy of the air (treated as an ideal gas) contained in a room remains constant as the temperature changes between day and night. Assume that the atmospheric pressure around remains constant and the air in the room maintains this pressure by communicating with the surrounding through the windows, doors, etc.
Use R = 8.314 J K-1 mol-1.
We Know internal energy at a particular temperature
Air in home is are chiefly diatomic molecules , so
Now by eqn. of state
Now pressure P is Constant also V of the room = constant
Thus, U = Constant.
Q.40. Figure shows a cylindrical tube of radius 5 cm and length 20 cm. It is closed by a tight-fitting cork. The friction coefficient between the cork and the tube is 0.20. The tube contains an ideal gas at a pressure of 1 atm and a temperature of 300 K. The tube is slowly heated and it is found that the cork pops out when the temperature reaches 600 K. Let dN denote the magnitude of the normal contact force exerted by a small length dlof the cork along the periphery (see the figure). Assuming that the temperature of the gas is uniform at any instant, calculate dN/dt.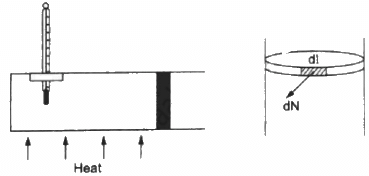
Here,
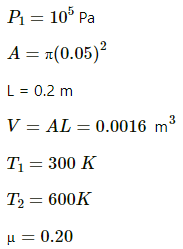
Applying 5 variable equation of state , we get
Applying law of friction , we get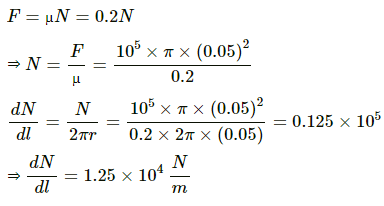
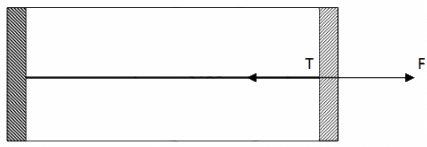
Q.41. Figure shows a cylindrical tube of cross-sectional area A fitted with two frictionless pistons. The pistons are connected to each other by a metallic wire. Initially, the temperature of the gas is T0 and its pressure is p0 which equals the atmospheric pressure. (a) What is the tension in the wire? (b) What will be the tension if the temperature is increased to 2T0 ?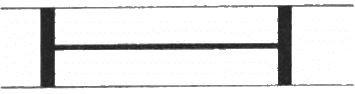
(a)
Since pressure from outside and inside the cylinder is the same, there is no net pressure acting on the pistons. So, tension will be zero.
(b)
Let the Pistons be L distance apart .
V = AL
Applying five variable gas equation , we get
By the free body diagram , we get
Q.42. Figure shows a large closed cylindrical tank containing water. Initially the air trapped above the water surface has a height h0 and pressure 2p0 where p0 is the atmospheric pressure. There is a hole in the wall of the tank at a depth h1 below the top from which water comes out. A long vertical tube is connected as shown. (a) Find the height h2 of the water in the long tube above the top initially. (b) Find the speed with which water comes out of the hole. (c) Find the height of the water in the long tube above the top when the water stops coming out of the hole.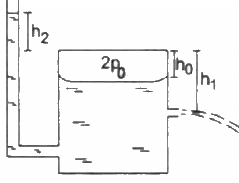
(a) Pressure of water above the water level of the bigger tank is given by
Let the atmospheric pressure above the tube be P0.
Total pressure above the tube = P0 + P
This pressure initially is balanced by pressure above the tank 2P0.
(b) Velocity of the efflux out of the outlet depends upon the total pressure above the outlet.Total pressure above the outlet =
Applying Bernouli's law, we get
Let the velocity of efflux be v1 and the velocity with which the level of the tank falls be v2 . pressure above the outlet is P0. Then,
Now , let the reference point of the liquid be the level of the outlet . Thus, z = 0
Again , the speed with which the water level of the tank goes down is very less compared to the velocity of the efflux . Thus, v2 = 0
(c) Water maintains its own level , so height of the water of the tank will be h1 when water will stop flowing
Thus height of water in the tube below the tank height will be = h1
Hence height of the water above the tank height will be = -h1.
Q.43. An ideal gas is kept in a long cylindrical vessel fitted with a frictionless piston of cross-sectional area 10 cm2 and weight 1 kg in figure. The vessel itself is kept in a big chamber containing air at atmospheric pressure 100 kPa. The length of the gas column is 20 cm. If the chamber is now completely evacuated by an exhaust pump, what will be the length of the gas column? Assume the temperature to remain constant throughout the process.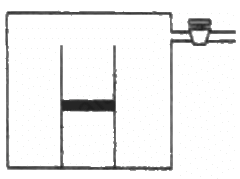
Atmospheric pressure inside the cylinderical vessel,
A = 10 cm2 = 10 × 10-4 m2
Pressure due to the weight of the piston
After evacution , external pressure above the piston = 0
Let L be the final length of the gas column . Then,
L = 2.2 m
Q.44. An ideal gas is kept in a long cylindrical vessel fitted with a frictionless piston of cross-sectional area 10 cm2 and weight 1 kg. The length of the gas column in the vessel is 20 cm. The atmospheric pressure is 100 kPa. The vessel is now taken into a spaceship revolving round the earth as a satellite. The air pressure in the spaceship is maintained at 100 kPa. Find the length of the gas column in the cylinder.
Use R = 8.3 J K-1 mol-1.
Here,
(a) Let x be the amount of water that evaporates.
P = RH × SVP
⇒ P = 0.4 × 1600 = 640
water will evaporate until VP becomes equal to SVP.
⇒ x ≈ 361 g
b) T = 288 + 5 = 293K
SVP = 2400 Pa
Difference in presssure = 2400 - 1600 = 800 Pa
Let x be the amount of water that evaporates.
⇒ x ≈ 296 g.
Q.45. Two glass bulbs of equal volume are connected by a narrow tube and are filled with a gas at 0°C at a pressure of 76 cm of mercury. One of the bulbs is then placed in melting ice and the other is placed in a water bath maintained at 62°C. What is the new value of the pressure inside the bulbs? The volume of the connecting tube is negligible.
Here,
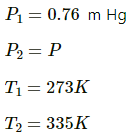
Let each of the bulbs have n1 moles initially.
Let the number of moles left in second bulb after its pressure reached P be n2.
Applying equation of state , we get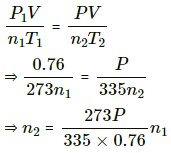
Number of moles left in the second bulb after the temperature rose = n1 - n2
Let n3 moles be left when pressure reached P . Applying equation of state in the first bulb , we get
n3 = its own n1 moles + the it received from the first
⇒ P = 0.8375
⇒ P = 84 cm of Hg
Q.46. The weather report reads, "Temperature 20°C : Relative humidity 100%". What is the dew point?
Here,
Relative humidity = 100%
⇒ Vapour pressure of air = SVP at the same temperature
So , the air is saturated at 20°C. So , dew point is 20°C.
Q.47. The condition of air in a closed room is described as follows. Temperature = 25°C, relative humidity = 60%, pressure = 104 kPa. If all the water vapour is removed from the room without changing the temperature, what will be the new pressure? The saturation vapour pressure at 25°C − 3.2 kPa.
Here,
T = 298 K
RH = 60%
= 0.6
Saturated vapour pressure
⇒ vapour pressure of water vapour
If the water vapour is completely removed from the air , then net pressure =
Q.48. The temperature and the dew point in an open room are 20°C and 10°C. If the room temperature drops to 15°C, what will be the new dew point?
Here,
Temperature = 20°C
Dew Point = 10°C
Air becomes saturated at 10°C. But if the room temperature is lowered to 15°C, the Dew point will still be at 10°C.
Q.49. Pure water vapour is trapped in a vessel of volume 10 cm3. The relative humidity is 40%. The vapour is compressed slowly and isothermally. Find the volume of the vapour at which it will start condensing.
Here,
RH = 40%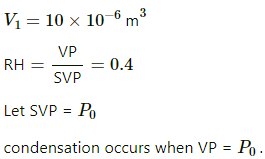
Since the process is isothermal , applying Boyle's law we get
Thus water vapour condenses at volume 4.0cm3.
Q.50. A barometer tube is 80 cm long (above the mercury reservoir). It reads 76 cm on a particular day. A small amount of water is introduced in the tube and the reading drops to 75.4 cm. Find the relative humidity in the space above the mercury column if the saturation vapour pressure at the room temperature is 1.0 cm.
Here ,
Atmospheric pressure , P = 0.76 m Hg
pressure due to water vapour inside ,
Vapour pressure =
SVH = 0.01 mHg
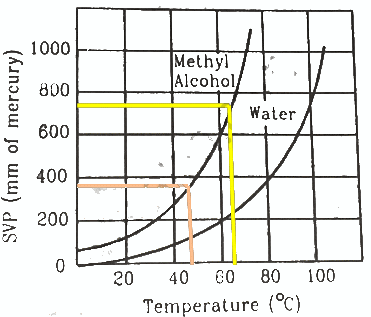
Q.51. Using figure, find the boiling point of methyl alcohol at 1 atm (760 mm of mercury) and at 0.5 atm.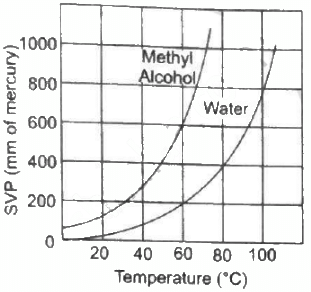
We drop a perpendicular on x-axis corresponding to the saturated vapour pressure 760 mm. This gives the boiling point 65° of methyl alcohol.
For 0.5 atm pressure, corresponding pressure in mm Hg will be 375 mm. We drop a perpendicular on x-axis corresponding to the saturated vapour pressure 375 mm. This gives the boiling point 48° of methyl alcohol.
Q.52. The human body has an average temperature of 98°F. Assume that the vapour pressure of the blood in the veins behaves like that of pure water. Find the minimum atmospheric pressure which is necessary to prevent the blood from boiling. Use figure for the vapour pressures.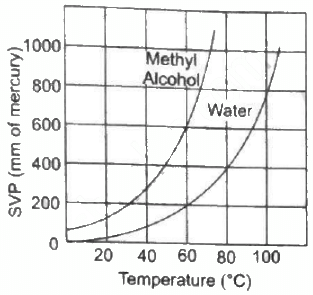
Here ,
T = 98°F
When we convert the temperature to °C , we get
We drop perpendicular corresponding to a temperature of 36.7°C on Y-axis from the curve of pure water. This gives the boiling point of blood 50 mm of Hg.
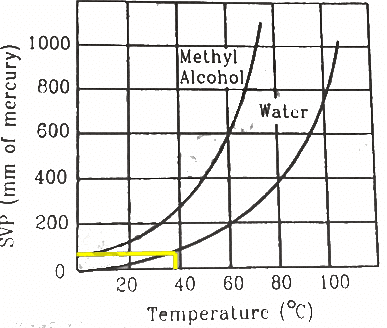
Q.53. A glass contains some water at room temperature 20°C. Refrigerated water is added to it slowly. when the temperature of the glass reaches 10°C, small droplets condense on the outer surface. Calculate the relative humidity in the room. The boiling point of water at a pressure of 17.5 mm of mercury is 20°C and at 8.9 mm of mercury it is 10°C.
Here,
Dew point = 10° C [∵ Dew appears at 10° C]
At boiling point, SVP equals atmospheric pressure.
At 20° C SVP = 17.5 mmHg
At dew point , SVP = 8.9 mmHg
= 51%.
Q.54. 50 m3 of saturated vapour is cooled down from 30°C to 20°C. Find the mass of the water condensed. The absolute humidity of saturated water vapour is 30 g m−3 at 30°C and 16 g m−3 at 20°C.
We Know that 1m3 of air contains 30 g of water vapour at 30°C.
So, amount of water vapour in 50 m3 of air at 30°C = (30 x 50)g = 1500g
Also , 1 m3 of air contains 16 g of water vapour at 20°C.
Amount of water vapour in 50m3 of air at
Amount of water vapour condensed = (1500 - 800) g = 700 g.
Q.55. A barometer correctly reads the atmospheric pressure as 76 cm of mercury. Water droplets are slowly introduced into the barometer tube by a dropper. The height of the mercury column first decreases and then becomes constant. If the saturation vapour pressure at the atmospheric temperature is 0.80 cm of mercury, find the height of the mercury column when it reaches its minimum value.
Atmospheric pressure = 76 cm Hg
SVP = 0.80 cm Hg
When water is introduced into the barometer, water evaporates.
Thus, it exerts its vapour pressure over the mercury meniscus.
As more and more water evaporates, the vapour pressure increases that forces down the mercury level further.
Finally, when the volume is saturated with the vapour at the atmospheric temperature, the highest vapour pressure, i.e. SVP is observed and the fall of mercury level reaches its minimum. Thus,
Net pressure acting on the column = 76 - 0.80 cmHg
Net length of Hg column at SVG = 75.2 cm
Q.56. 50 cc of oxygen is collected in an inverted gas jar over water. The atmospheric pressure is 99.4 kPa and the room temperature is 27°C. The water level in the jar is same as the level outside. The saturation vapour pressure at 27°C is 3.4 kPa. Calculate the number of moles of oxygen collected in the jar.
Here ,
Now,
Pressure inside the jar = Pressure outside the jar [∵ Level of water is same inside and outside of the jar]
Pressure outside the jar = Atmospheric pressure
Pressure inside the jar = VP of oxygen + SVP of water at 27°C
Applying equation of state , we get
PV = nRT
Q.57. A faulty barometer contains certain amount of air and saturated water vapour. It reads 74.0 cm when the atmospheric pressure is 76.0 cm of mercury and reads 72.10 cm when the atmospheric pressure is 74.0 cm of mercury. Saturation vapour pressure at the air temperature = 1.0 cm of mercury. Find the length of the barometer tube above the mercury level in the reservoir.
Given :
Let the CSA be A.
case 1 :
V1 = (x - 74)A
SVP = 1 cm Hg
Atmospheric pressure, P0 = 76 cm HgMercury column height = 74.0 cm
Let P be the air pressure above the barometer. Then,
Atmospheric pressure = SVP + Air pressure above the barometer mercury level + Mercury column height
⇒ 1+P+74 = 76
⇒ P = 1 cm
case 2 :
Atmospheric pressure, P0, = 74.0 cm Hg
Let P' be the air pressure. Then,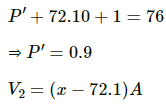
Applying Boyle's law, we get
Length of the tube = 91.1 cm.
Q.58. On a winter day, the outside temperature is 0°C and relative humidity 40%. The air from outside comes into a room and is heated to 20°C. What is the relative humidity in the room? The saturation vapour pressure at 0°C is 4.6 mm of mercury and at 20°C it is 18 mm of mercury.
Given :
SVP at 0°C = 4.6 mm Hg
RH = 40%
Here, V is constant .
Applying equation of state, we get
SVP at the same temperature = 18 mmHg
Q.59. The temperature and humidity of air are 27°C and 50% on a particular day. Calculate the amount of vapour that should be added to 1 cubic metre of air to saturate it. The saturation vapour pressure at 27°C = 3600 Pa.
Use R = 8.3 J K-1 mol-1.
Here ,
SVP = 3600 Pa
T = 273 + 27 = 300K
V = 1m3
M = 18 g for water
RH = 50%
Let m1 be the mass of water present in the 50% humid air.
Required pressure for saturation = 3600 Pa
Let m2 be the amount of water required for saturation .
Total excess water vapour that has to be added = m2 - m1
⇒ 36 - 13 = 13 g
Q.60. The temperature and relative humidity in a room are 300 K and 20% respectively. The volume of the room is 50 m3. The saturation vapour pressure at 300 K 3.3 kPa. Calculate the mass of the water vapour present in the room.
Use R = 8.3 J K-1 mol-1.
Here,
T = 300K
SVP = 3300 Pa at 300K
RH = 20%
V = 50 m3
M = 18 g
Now,
PV = nRT
⇒ m = 238.55 g≈238 g
Q.61. The temperature and the relative humidity are 300 K and 20% in a room of volume 50 m3. The floor is washed with water, 500 g of water sticking on the floor. Assuming no communication with the surrounding, find the relative humidity when the floor dries. The changes in temperature and pressure may be neglected. Saturation vapour pressure at 300 K = 3.3 kPa.
Use R = 8.31 J K-1 mol-1.
Here,
M = 18g for water
m = 500g
V = 50 m3
T = 300K
SVP = 3300 Pa
RH = 20%
Partial pressure P2 For evaporated water is given by
Q.62. A bucket full of water is placed in a room at 15°C with initial relative humidity 40%. The volume of the room is 50 m3. (a) How much water will evaporate? (b) If the room temperature is increased by 5°C, how much more water will evaporate? The saturation vapour pressure of water at 15°C and 20°C are 1.6 kPa and 2.4 kPa respectively.
Use R = 8.3 J K-1 mol-1.
(a) Relative humidity is given by
Evaporation occurs as long as the atmosphere is not saturated.
Let the mass of water evaporated be m. Then,
Net pressure change =
Mass of water evaporated is given by
= 296.06 ≈ 296 g
|
134 docs
|