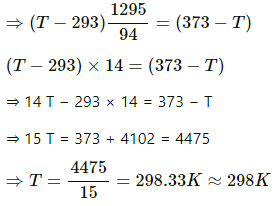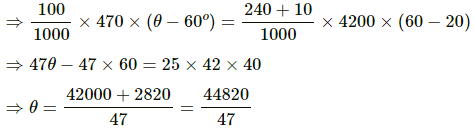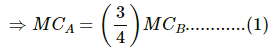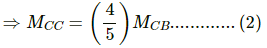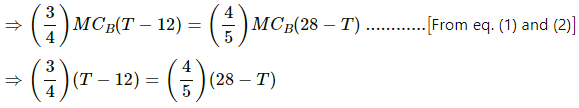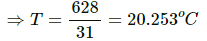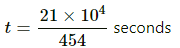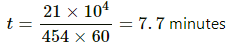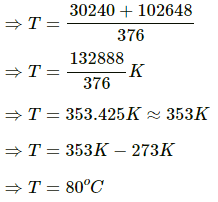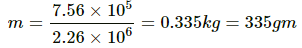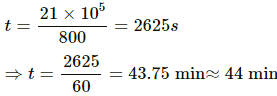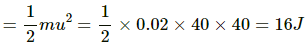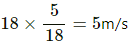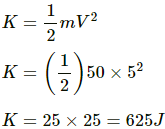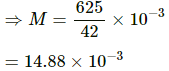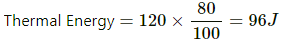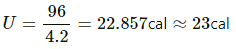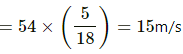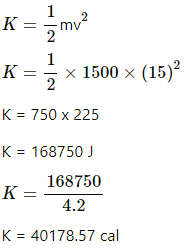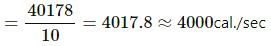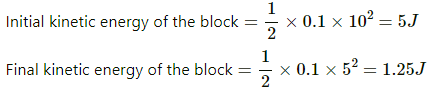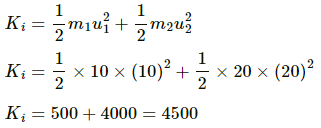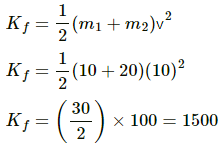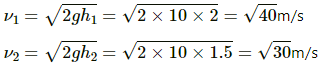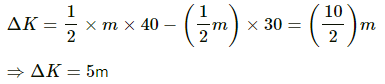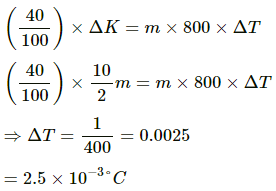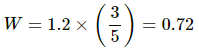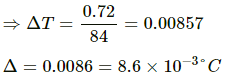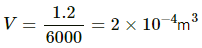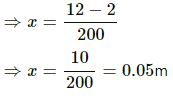HC Verma Questions and Solutions: Chapter 25: Calorimetry- 2 | HC Verma Solutions - JEE PDF Download
Exercises
Q.1. An aluminium vessel of mass 0.5 kg contains 0.2 kg of water at 20°C. A block of iron of mass 0.2 kg at 100°C is gently put into the water. Find the equilibrium temperature of the mixture. Specific heat capacities of aluminium, iron and water are 910 J kg−1 K−1, 470 J kg−1 K−1 and 4200 J kg−1 K−1 respectively.
Given:-
Mass of aluminium = 0.5 kg
Mass of water = 0.2 kg
Mass of iron = 0.2 kg
Specific heat of aluminium = 910 J kg−1 K−1
Specific heat of iron = 470 J kg−1 K−1
Specific heat of water = 4200 J kg−1 K−1
Let the equilibrium temperature of the mixture be T.
Temperature of aluminium and water = 20°C = 273+20 = 293 K
Temperature of iron = 100°C = 273 + 100 = 373 K
Heat lost by iron, H1 = 0.2 × 470 × (373 − T)
Heat gained by water = 0.2 × 4200 × (T − 293)
Heat gained by iron = 0.5 × 910 × (T−293)
Total heat gained by water and iron, H2 = 0.5 × 910 (T−293) + 0.2 × 4200 × (T − 293)
H2 = (T − 293) [0.5 × 910 + 0.2 × 4200]
We know,
Heat gain = Heat lost
⇒ (T − 293) [0.5 × 910 + 0.2 × 4200] = 0.2 × 470 × (373 −T)
⇒ (T − 293) (455 + 840) = 94 (373 − T)
∴ T = (298 − 273)°C = 25°C
∴ Final temperature = 25° C
Q.2. A piece of iron of mass 100 g is kept inside a furnace for a long time and then put in a calorimeter of water equivalent 10 g containing 240 g of water at 20°C. The mixture attains and equilibrium temperature of 60°C. Find the temperature of the furnace. Specific heat capacity of iron = 470 J kg−1 °C−1.
Given:-
Mass of iron = 100 g
Water equivalent of calorimeter = 10 g
Mass of water = 240 gm
Let the temperature of surface be θ°C.
Specific heat capacity of iron = 470 J kg−1 °C−1
Total heat gained = Total heat lost
= 953.61°C
Q.3. The temperatures of equal masses of three different liquids A, B and C are 12°C, 19°C and 28°C respectively. The temperature when A and B are mixed is 16°C, and when B and C are mixed, it is 23°C. What will be the temperature when A and C are mixed?
Given:
Temperature of A = 12°C
Temperature of B = 19°C
Temperature of C = 28°C
Temperature of mixture of A and B = 16°C
Temperature of mixture of B and C = 23°C
Let the mass of the mixtures be M and the specific heat capacities of the liquids A, B and C be CA, CB, and CC, respectively.
According to the principle of calorimetry, when A and B are mixed, we get
Heat gained by Liquid A = Heat lost by liquid B
⇒ MCA (16 − 12) = MCB (19 − 16)
⇒ 4MCA = 3 MCB
When B and C are mixed:
Heat gained by liquid B = Heat lost by liquid C
⇒ MCB (23 − 19) = MCC (28 − 23)
⇒ 4MCB = 5 MCC
When A and C are mixed:
Let the temperature of the mixture be T. Then,
Heat gained by liquid A = Heat lost by liquid C
⇒ MCA (T − 12) = MCC (28 − T)
Using the values of MCA and MCC, we get
⇒ (3×5) (T−12) = (4×4) (28−T)
⇒ 15T−180 = 448−16T
⇒ 31T = 628
⇒T = 20.3°C
Q.4. Four 2 cm × 2 cm × 2 cm cubes of ice are taken out from a refrigerator and are put in 200 ml of a drink at 10°C. (a) Find the temperature of the drink when thermal equilibrium is attained in it. (b) If the ice cubes do not melt completely, find the amount melted. Assume that no heat is lost to the outside of the drink and that the container has negligible heat capacity. Density of ice = 900 kg m−3, density of the drink = 1000 kg m−3, specific heat capacity of the drink = 4200 J kg−1 K−1, latent heat of fusion of ice = 3.4 × 105 J kg−1.
(a)
Given:-
Number of ice cubes = 4
Volume of each ice cube = (2 × 2 × 2) = 8 cm3
Density of ice = 900 kg m−3
Total mass of ice, mi = (4 × 8 ×10−6 ×900) = 288×10−4 kg
Latent heat of fusion of ice, Li = 3.4 × 105 J kg−1
Density of the drink = 1000 kg m−3
Volume of the drink = 200 ml
Mass of the drink = (200×10−6)×1000 kg
Let us first check the heat released when temperature of 200 ml changes from 10oC to 0oC.
Hw = (200×10−6)×1000×4200×(10−0) = 8400 J
Heat required to change four 8 cm3 ice cubes into water (Hi) = miLi = (288×10−4)×(3.4×105) = 9792 J
Since the heat required for melting the four cubes of the ice is greater than the heat released by water ( Hi > Hw ), some ice will remain solid and there will be equilibrium between ice and water. Thus, the thermal equilibrium will be attained at 0°C.
(b)
Equilibrium temperature of the cube and the drink = 0°C
Let M be the mass of melted ice.
Heat released when temperature of 200 ml changes from 10°C to 0°C is given by
Hw = (200×10−6)×1000×4200×(10−0) = 8400 J
Thus,
M×(3.4×105) = 8400 J
Therefore,
M = 0.0247 Kg = 25 g.
Q.5. Indian style of cooling drinking water is to keep it in a pitcher having porous walls. Water comes to the outer surface very slowly and evaporates. Most of energy needed for evaporation is taken from the water itself and the water is cooled down. Assume that a pitcher contains 10 kg of water and 0.2 g of water comes out per second. Assuming no backward heat transfer from the atmosphere to the water, calculate the time in which the temperature decrease by 5°C. Specific heat capacity of water = 4200 J kg−1 °C−1 and latent heat of vaporization of water = 2.27 × 106 J kg−1.
Given:-
Specific heat of water ,S = 4200 J kg−1 °C−1
Latent heat of vapourisation of water ,L = 2.27 × 106 J kg−1
Mass, M = 0.2 g = 0.0002 kg
Let us first calculate the amount of energy required to decrease the temperature of 10 kg of water by 5°C.
U1 = 10 × 4200 J/kg°C × 5°C
U1 = 210,000 = 21 × 104 J
Let the time in which the temperature is decreased by 5°C be t.
Energy required per second for evaporation of water (at the rate of 0.2 g/sec) is given by
U2 = ML
U2 = (2 × 10−4 )× (2.27 × 106) = 454 J
Total energy required to decrease the temperature of the water = 454 × t
= 21 × 104 J
Now,
The time taken in minutes is given by
∴ The time required to decrease the temperature by 5°C is 7.7 minutes.
Q.6. A cube of iron (density = 8000 kg m−3, specific heat capacity = 470 J kg−1 K−1) is heated to a high temperature and is placed on a large block of ice at 0°C. The cube melts the ice below it, displaces the water and sinks. In the final equilibrium position, its upper surface just goes inside the ice. Calculate the initial temperature of the cube. Neglect any loss of heat outside the ice and the cube. The density of ice = 900 kg m−3 and the latent heat of fusion of ice = 3.36 × 105 J kg−1.
Given:-
Density of the iron cube = 8000 kg m-3
Density of the ice cube = 900 kg m-3
Specific heat capacity, S = 470 J kg−1 K−1
Latent heat of fusion of ice, L = 3.36 × 105 J kg−1
Let the volume of the cube be V.
Volume of water displaced = V
Mass of cube, m = 8000 V kg
Mass of the ice melted, M = 900 V
Let the initial temperature of the iron cube be T K.
Then,
Heat gained by the ice = Heat lost by the iron cube
m × S × (T − 273) = M × L
⇒ 8000 V × 470 × (T − 273) = 900 V×( 3.36 × 105)
⇒ 376 × 104 × (T − 273) = 3024 × 105
Q.7. 1 kg of ice at 0°C is mixed with 1 kg of steam at 100°C. What will be the composition of the system when thermal equilibrium is reached? Latent heat of fusion of ice = 3.36 × 103 J kg−1 and latent heat of vaporization of water = 2.26 × 106 J kg−1.
Given:-
Amount of ice at 0oC = 1 kg
Amount of steam at 100oC = 1 kg
Latent heat of fusion of ice = 3.36 × 103 J kg−1
Latent heat of vapourisation of water = 2.26 × 106 J kg−1
We can observe that the latent heat of fusion of ice (3.36 × 105 J kg−1) is smaller that latent heat of vapouisation of water (2.26 × 106 ). Therefore, ice will first change into water as less heat is required for this and there will be equilibrium between steam and water.
Heat absorbed by the ice when it changes into water (Q1) = 1×(3.36 × 105) J
Heat absorbed by the water formed to change its temperature from 0°C to 100°C (Q2) = 1 × 4200 × 100 = 4.2 × 105 J
Total heat absorbed by the ice to raise the temperature to 100°C, Q = Q1+Q2 = 3.36 × 105+ 4.2 × 105 = (3.36 + 4.2) × 105 = 7.56 × 105 J
The heat required to change ice into water at 100°C is supplied by the steam. This heat will be released by the steam and will then change into water.
If all the steam gets converted into water, heat released by steam, Q' = 1 ×( 2.26 × 106) J = 2.26 × 106 J
Amount of heat released is more than that required by the ice to get converted into water at 100oC. Thus,
Extra heat = Q − Q'
= (2.26 − 0.756) × 106
= 1.506 × 106
Let the mass of steam that is condensed into water be m. Thus,
Total amount of water at 100°C = 1000 + 335 = 1335 g =1.335 g
Steam left = 1− 0.335 = 0.665 kg = 665 gm
Q.8. Calculate the time required to heat 20 kg of water from 10°C to 35°C using an immersion heater rated 1000 W. Assume that 80% of the power input is used to heat the water. Specific heat capacity of water = 42000 J kg−1 K−1.
Given:-
Power rating of the immersion rod, P = 1000 W
Specific heat of water, S = 4200 J kg−1 K−1
Mass of water, M = 20 kg
Change in temperature, ΔT = 25 °C
Total heat required to raise the temperature of 20 kg of water from 10°C to 35°C is given by
Q = M × S × ΔT
Q = 20 × 4200 × 25
Q = 20 × 4200 × 25 = 21 × 105 J
Let the time taken to heat 20 kg of water from 10°C to 35°C be t. Only 80% of the immersion rod's heat is useful for heating water. Thus,
Energy of the immersion rod utilised for heating the water = t × (0.80) × 1000 J
t × (0.80) × 1000 J = 21 × 105 J
Q.9. On a winter day the temperature of the tap water is 20°C whereas the room temperature is 5°C. Water is stored in a tank of capacity 0.5 m3 for household use. If it were possible to use the heat liberated by the water to lift a 10 kg mass vertically, how high can it be lifted as the water comes to the room temperature? Take g = 10 m s−2.
Given:-
Initial temperature of the water, Ti = 20°C
Final temperature of the water (room temperature), Tf = 5°C
Change in temeprature, ΔT = 20°C − 5°C = 15°C
Volume of water = 0.5 m3
Density of water, d = 1000 kg/m3
Mass of the water, M = (0.5 × 1000) kg = 500 kg
Heat liberated as the temperature of water changes from 20°C to 5°C is given by
Q = M×S×ΔT
Q = (500 × 4200 × 15) J
Q = (500 × 4200 × 15) J
Q = (75 × 420 × 1000) J
Q = 31500 × 1000 J = 315×105 J
Let the height to which the mass is lifted be h.
The energy required to lift the block = mgh = 10 × 10 × h = 100 h
Acording to the question,
Q = mgh
⇒ 100 h = 315×105 J
⇒ h = 315×103 m = 315 km
Q.10. A bullet of mass 20 g enters into a fixed wooden block with a speed of 40 m s−1 and stops in it. Find the change in internal energy during the process.
Given:-
Mass of bullet, m = 20g = 0.02 kg
Initial velocity of the bullet, u = 40 m/s
Final velocity of the bullet = 0 m/s
Initial kinetic energy of the bullet
Final kinetic energy of the bullet = 0
Change in energy of the bullet = 16 J
It is given that the bullet enters the block and stops inside it. The total change in its kinetic energy is responsible for the change in the internal energy of the block.
∴ Change in internal energy of the block = Change in energy of the bullet = 16 J
Q.11. A 50 kg man is running at a speed of 18 km h−1. If all the kinetic energy of the man can be used to increase the temperature of water from 20°C to 30°C, how much water can be heated with this energy?
Given:-
Mass of the man, m = 50 kg
Speed of the man, v = 18 km/h =
Kinetic energy of the man is given by
Specific heat of the water, s = 4200 J/Kg-K
Let the mass of the water heated be M.
The amount of heat required to raise the temperature of water from 20°C to 30°C is given by
Q = msΔT = M × 4200 × (30 − 20)
Q = 42000 M
According to the question,
Q = K
42000 M = 625
=15 kg
Q.12. A brick weighing 4.0 kg is dropped into a 1.0 m deep river from a height of 2.0 m. Assuming that 80% of the gravitational potential energy is finally converted into thermal energy, find this thermal energy is calorie.
Given:-
Mass of the brick, m = 4 kg
Total vertical distance travelled by the brick, h = 3 m
Percentage of gravitational potential energy converted to thermal energy = 80
Total change in potential energy of the brick = mgh = 4 × 10 × 3 = 120 J
Thermal energy in calories is given by
Q.13. A van of mass 1500 kg travelling at a speed of 54 km h−1 is stopped in 10 s. Assuming that all the mechanical energy lost appears as thermal energy in the brake mechanism, find the average rate of production of thermal energy is cal s−1.
Given:-
Mass of van, m = 1500 kg
Speed of van, v = 54 km/h
Total kinetic energy of the van is given by
Loss in total energy of the van = 40178 cal
Loss in energy per second
∴ Average rate of production of thermal energy ≈ 4000 cal/sec
Q.14. A block of mass 100 g slides on a rough horizontal surface. If the speed of the block decreases from 10 m s−1 to 5 m s−1, find the thermal energy developed in the process.
Given:-
Mass of the block = 100 g = 0.1 kg
Initial speed of the block = 10 m/s
Final speed of the block = 5 m/s
Change in kinetic energy of the block = 5 - 1.25 = 3.75 J
Thermal energy developed is equal to the change in kinetic energy of the block. Thus,
Thermal energy developed in the process = 3.75 J
Q.15. The blocks of masses 10 kg and 20 kg moving at speeds of 10 m s−1 and 20 m s−1 respectively in opposite directions, approach each other and collide. If the collision is completely inelastic, find the thermal energy developed in the process.
Given:-
Mass of the first block, m1 = 10 kg
Mass of the second block, m2 = 20 kg
Initial velocity of the first block, u1 = 10 m/s
Initial velocity of the second block, u2 = 20 m/s
Let the velocity of the blocks after collision be v.
Applying conservation of momentum, we get
m2u2 − m1u1 = (m1 + m2)v
⇒ 20 × 20 − 10 × 10 = (10 + 20)v
⇒ 400 − 100 = 30 v
⇒ 300 = 30 v
⇒ v = 10 m/s
Initial kinetic energy is given by
Final kinetic energy is given by
∴ Total change in KE = 4500 J − 1500 J = 3000 J
Thermal energy developed in the process = 3000 J
Q.16. A ball is dropped on a floor from a height of 2.0 m. After the collision it rises up to a height of 1.5 m. Assume that 40% of the mechanical energy lost goes as thermal energy into the ball. Calculate the rise in the temperature of the ball in the collision. Heat capacity of the ball is 800 J K−1.
Height of the floor from which ball is dropped, h1 = 2.0 m
Height to which the ball rises after collision, h2 = 1.5 m
Let the mass of ball be m kg.
Let the speed of the ball when it falls from h1 and h2 be v1 and v2, respectively.
Change in kinetic energy is given by
If the position of the ball is considered just before hitting the ground and after its first collision, then 40% of the change in its KE will give the change in thermal energy of the ball. At these positions, the PE of the ball is same. Thus,
Loss in PE = 0
The change in kinetic energy is utilised in increasing the temperature of the ball.
Let the change in temperature be ΔT. Then,
Q.17. A copper cube of mass 200 g slides down on a rough inclined plane of inclination 37° at a constant speed. Assume that any loss in mechanical energy goes into the copper block as thermal energy. Find the increase in the temperature of the block as it slides down through 60 cm. Specific heat capacity of copper = 420 J kg−1 K−1.
Mass of copper cube, m = 200 g = 0.2 kg
Length through which the block has slided, l = 60 cm = 0.6 m
Since the block is moving with constant velocity, the net force on it is zero. Thus,
Force of friction, f = mg
Also, since the object is moving with a constant velocity, change in its K.E will be zero.As the object slides down, its PE decreases at the cost of increase in thermal energy of copper.
The loss in mechanical energy of the copper block = Work done by the frictional force on the copper block to a distance of 60 cm
W = mg l sin θ
W = 0.2 × 10 × 0.6 sin 37°
Let the change in temperature of the block be ∆T.
Thermal energy gained by block = ms ∆T = 0.2 × 420×∆T = 84∆T
But 84∆T = 0.72
Q.18. A metal block of density 600 kg m−3 and mass 1.2 kg is suspended through a spring of spring constant 200 N m−1. The spring-block system is dipped in water kept in a vessel. The water has a mass of 260 g and the bloc is at a height 40 cm above the bottom of the vessel. If the support of the spring is broken, what will be the rise in the temperature of the water. Specific heat capacity of the block is 250 J kg−3 K−1 and that of water is 4200 J kg−1 K−1. Heat capacities of the vessel and the spring are negligible.
Given:-
Density of metal block, d = 600 kg m−3
Mass of metal block, m = 1.2 kg
Spring constant of the spring, k = 200 N m−1
Volume of the block,
When the mass is dipped in water, it experiences a buoyant force and in the spring there is potential energy stored in it.
If the net force on the block is zero before breaking of the support of the spring, then
kx + Vρg = mg
200x + (2 × 10−4)× (1000) × (10) = 12
The mechanical energy of the block is transferred to both block and water. Let the rise in temperature of the block and the water be ΔT.
Applying conservation of energy, we get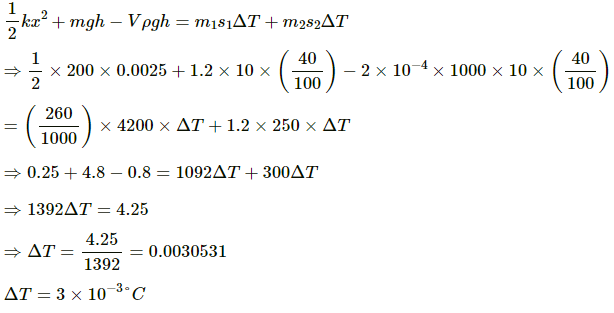
|
134 docs
|
FAQs on HC Verma Questions and Solutions: Chapter 25: Calorimetry- 2 - HC Verma Solutions - JEE
| 1. What is calorimetry? |  |
| 2. How does a calorimeter work? |  |
| 3. What is the principle of constant pressure calorimetry? |  |
| 4. How is the heat capacity of a calorimeter determined? |  |
| 5. What are some applications of calorimetry? |  |