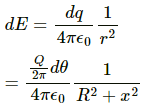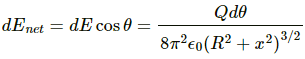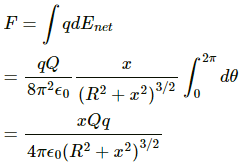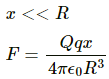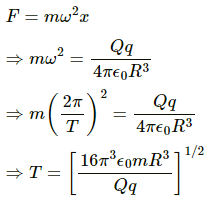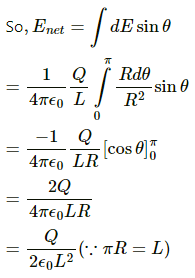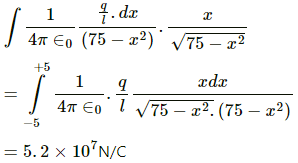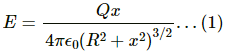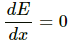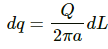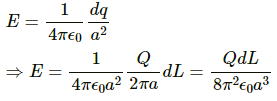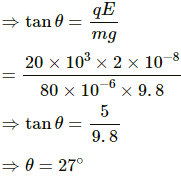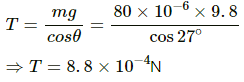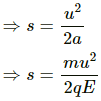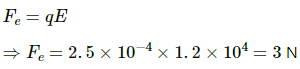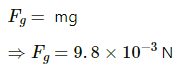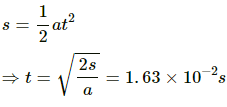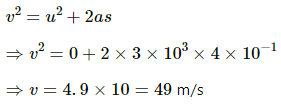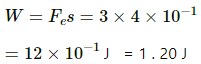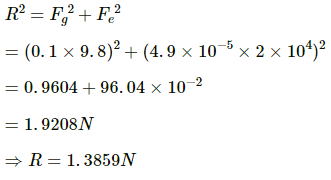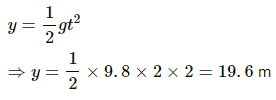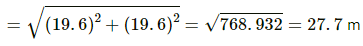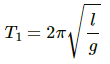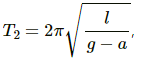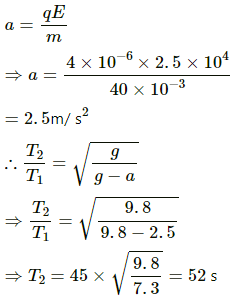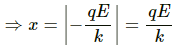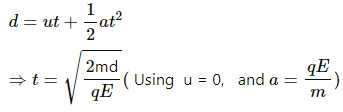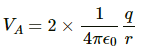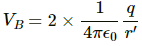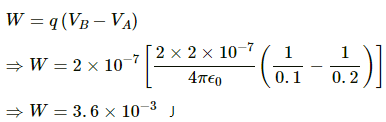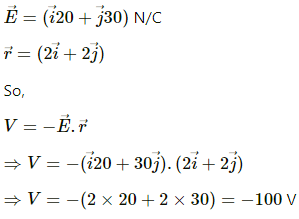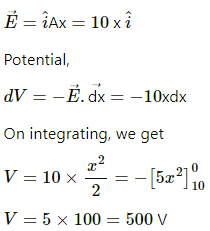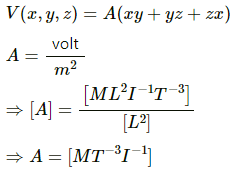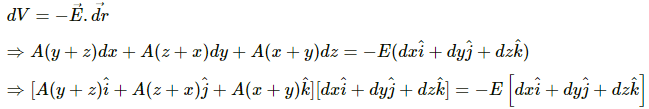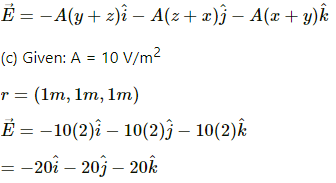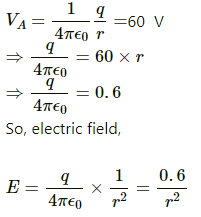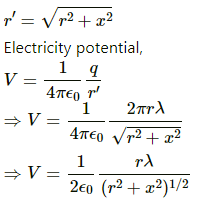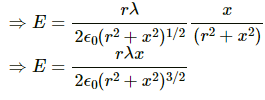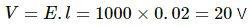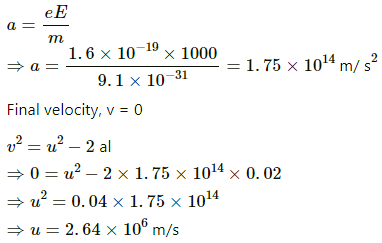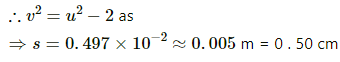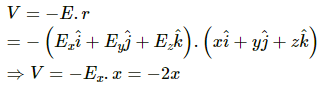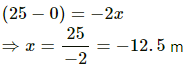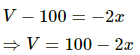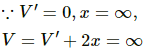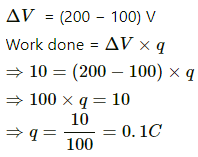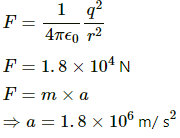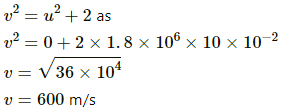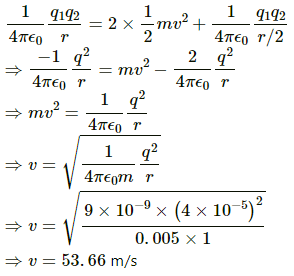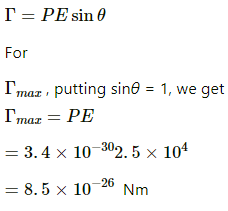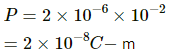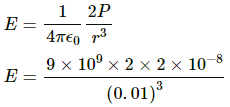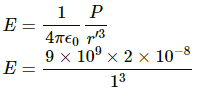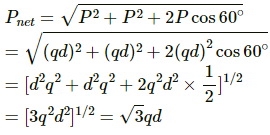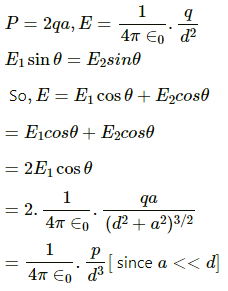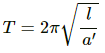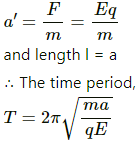HC Verma Questions and Solutions: Chapter 29: Electric Field & Potential- 3 | HC Verma Solutions - JEE PDF Download
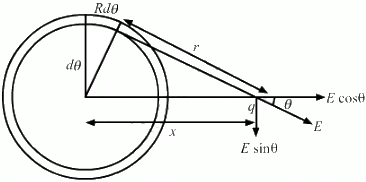
Q.39. A positive charge Q is distributed uniformly over a circular ring of radius R. A particle of mass m, and a negative charge q, is placed on its axis at a distance x from the centre. Find the force on the particle. Assuming x << R, find the time period of oscillation of the particle if it is released from there .
Consider an element of angular width dθ at a distance r from the charge q on the circular ring, as shown in the figure.
So, charge on the element,
Electric field due to this charged element,
By the symmetry, the E sinθ component of all such elements on the ring will vanish.
So, net electric field,
Total force on the charged particle,
According to the question,
Comparing this with the condition of simple harmonic motion, we get
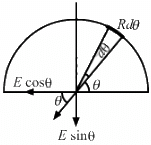
Q.40. A rod of length L has a total charge Q distributed uniformly along its length. It is bent in the shape of a semicircle. Find the magnitude of the electric field at the centre of curvature of the semicircle.
Consider an element of angular width dθ, as shown in the figure.
The net electric field has a vertical component only.
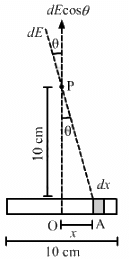
Q.41. A 10-cm long rod carries a charge of +50 μC distributed uniformly along its length. Find the magnitude of the electric field at a point 10 cm from both ends of the rod.
Net electric field = ∫dE cos θ
Q.42. Consider a uniformly charged ring of radius R. Find the point on the axis where the electric field is maximum.
Let the total charge of the ring be Q.
Radius of the ring = R
The electric field at distance x from the centre of ring,
For maximum value of electric field,
From equation (1),
Q.43. A wire is bent in the form of a regular hexagon and a total charge q is distributed uniformly on it. What is the electric field at the centre? You may answer this part without making any numerical calculations.
As the wire is bent to form a regular hexagon, it forms an equipotential surface, as shown in the figure.
Hence, the charge at each point is equal and the net electric field at the centre is 0.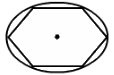
Q.44. A circular wire-loop of radius a carries a total charge Q distributed uniformly over its length. A small length dL of the wire is cut off. Find the electric field at the centre due to the remaining wire.
We know that the electric field is zero at the centre of a uniformly charged circular wire.
That is, the electric field due to a small element dl of wire + electric field due to the remaining wire = 0
Let the charge on the small element dl be dq. So,
Electric field due to a small element at the centre,
So, the electric field at the centre due to the remaining wire =(Opposite the direction of the electric field due to the small element)
Q.45. A positive charge q is placed in front of a conducting solid cube at a distance d from its centre. Find the electric field at the centre of the cube to the charges appearing on its surface.
Electric field at a point due to a given charge, E =
where q is the charge and R the distance between the point and the charge.
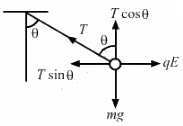
Q.46. A pendulum bob of mass 80 mg and carrying a charge of 2 × 10−8 C is at rest in a uniform, horizontal electric field of 20 kVm−1. Find the tension in the thread.
Given:
Magnitude of the charge, q = 2.0 × 10−8 C
Mass of the bob, m = 80 mg = 80 × 10−6 kg
Electric field, E = 20 kVm−1 = 20 × 103 Vm−1
Let the direction of the electric field be from the left to right. Tension in the string is T.
From the figure,
Tcosθ = mg ...(1)
Tsinθ = qE ...(2)
From equation (1),
Q.47. A particle of mass m and charge q is thrown at a speed u against a uniform electric field E. How much distance will it travel before coming to momentary rest ?
Given:
Charge of the particle = q
Velocity of projection = u
Electric field intensity = E
Mass of the particle = m
We know that the force experience by a charged particle in an electric field is qE.
Acceleration produced, a = qE/m (Negative because the particle is thrown against the electric field)
Let the distance covered by the particle be s.
Then v2 = u2 + 2as
[Here, a = deceleration, v = final velocity]
Here, 0 = u2 − 2as
Q.48.1. A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. Find the electric force and the force of gravity acting on this particle. Can one of these forces be neglected in comparison with the other for approximate analysis?
Given:
Charge of the particle, q = 2.5 × 10−4 C
Initial velocity, u = 0
Electric field intensity, E = 1.2 × 104 N/C
Mass of the particle, m = 1 g = 10−3 kg
Distance travelled, s = 40 cm = 4 × 10−1 m
Electric force,
Force of gravity,
Q.48.2. A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. How long will it take for the particle to travel a distance of 40 cm?
Given:
Charge of the particle, q = 2.5 × 10−4 C
Initial velocity, u = 0
Electric field intensity, E = 1.2 × 104 N/C
Mass of the particle, m = 1 g = 10−3 kg
Distance travelled, s = 40 cm = 4 × 10−1 m
Acceleration of the particle,
Let t be the time taken by the particle to cover the distance s = 40 cm. Then,
Q.48.3. A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. What will be the speed of the particle after travelling this distance?
Given:
Charge of the particle, q = 2.5 × 10−4 C
Initial velocity, u = 0
Electric field intensity, E = 1.2 × 104 N/C
Mass of the particle, m = 1 g = 10−3 kg
Distance travelled, s = 40 cm = 4 × 10−1 m
Using the third equation of motion, we get
Q.48.4. A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. How much is the work done by the electric force on the particle during this period?
Given:
Charge of the particle, q = 2.5 × 10−4 C
Initial velocity, u = 0
Electric field intensity, E = 1.2 × 104 N/C
Mass of the particle, m = 1 g = 10−3 kg
Distance travelled, s = 40 cm = 4 × 10−1 m
Work done by the electric force,
Q.49. A ball of mass 100 g and with a charge of 4.9 × 10−5 C is released from rest in a region where a horizontal electric field of 2.0 × 104 N C−1 exists. (a) Find the resultant force acting on the ball. (b) What will be the path of the ball? (c) Where will the ball be at the end of 2 s?
Given:
Charge of the ball, q = 4.9 × 10−5 C
Electrical field intensity, E = 2 × 104 N/C
Mass of the ball, m = 100 gm
Force of gravity, Fg = mg
Electrical force, Fe = Eq
The particle moves due to the resultant force of Fg and Fe.
Fg = Fe
⇒ tanθ = 1
⇒ θ = 45°
θ is the angle made by the horizontal with the resultant.
Hence, the path of the ball is straight and is along the resultant force at an angle of 45° with the horizontal
Vertical displacement in t = 2 s,
Both the forces are same.
So, vertical displacement in 2 s = Horizontal displacement in 2 s
Net displacement
Q.50. The bob of a simple pendulum has a mass of 40 g and a positive charge of 4.0 × 10−6 C. It makes 20 oscillations in 45 s. A vertical electric field pointing upward and of magnitude 2.5 × 104 NC−1 is switched on. How much time will it now take to complete 20 oscillations?
Given:
Charge of the particle, q = 4.0 × 10−6 C
Electrical field intensity, E = 2.5 × 104 NC−1
Mass of the particle, m = 40 g = 0.04 kg
When no electrical field is applied, time period,
When upward electrical field is applied, time period,
where a is the upward acceleration due to electrical field, which is given by
Q.51. A block of mass m with a charge q is placed on a smooth horizontal table and is connected to a wall through an unstressed spring of spring constant k, as shown in the figure. A horizontal electric field E, parallel to the spring, is switched on. Find the amplitude of the resulting SHM of the block.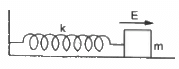
Given:
Charge of the block = q
Electrical field intensity = E
Mass of the block = m
Spring constant = k
Electric force, F = qE
Spring force, F = − kx (where x is the amplitude)
Therefore, qE = − kx
Q.52. A block of mass containing a net positive charge q is placed on a smooth horizontal table which terminates in a vertical wall as shown in the figure. The distance of the block from the wall is d. A horizontal electric field E towards the right is switched on. Assuming elastic collisions (if any), find the time period of the resulting oscillatory motion. Is it a simple harmonic motion?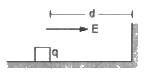
For motion to be simple harmonic,acceleration should be proportional to the displacement and should be directed in a direction opposite to the displacement.
When the block is moving towards the wall, the acceleration is along displacement.
So, the block does not undergo SHM.
Time taken to reach the wall is given by
Since it is an elastic collision, the time taken by the block to move towards the wall is the time taken to move away from it till the velocity is zero.
Total time, T = 2t
Q.53. A uniform electric field of 10 N C−1 exists in the vertically downward direction. Find the increase in the electric potential as one goes up through a height of 50 cm.
Electric field intensity, E = 10 N/C,
Change in height, ds = 50 cm = 1/2 m
Change in electric potential, dV = E.ds = 10 × 1/2 = 5V
Q.54. 12 J of work has to be done against an existing electric field to take a charge of 0.01 C from A to B. How much is the potential difference VB − VA?
Given:
Charge, q = 0.01 C,
Work done, W = 12 J
Now, work done = potential difference × charge
W = (VB − VA) × q
VB − VA = 12/0.01 = 1200 V
Q.55. Two equal charges, 2.0 × 10−7 C each, are held fixed at a separation of 20 cm. A third charge of equal magnitude is placed midway between the two charges. It is now moved to a point 20 cm from both the charges. How much work is done by the electric field during the process?
Let the third charge be moved from point A to point B.
Magnitude of the charges, q = 2.0 × 10−7 C
Distance of both the charges from point A, r = 10 cm =0.1 m
Distance of both the charges from point B, r' = 20 cm =0.2 m
Potential at A,
Potential at B,
Work done,
Q.56. An electric field of 20 NC−1 exists along the x-axis in space. Calculate the potential difference VB − VA where the points A and B are
(a) A = (0, 0); B = (4 m, 2m)
(b) A = (4 m, 2 m); B = (6 m, 5 m)
(c) A = (0, 0); B = (6 m, 5 m)
Do you find any relation between the answers of parts (a), (b) and (c)?
Given:
Electric field intensity, E = 20 N/C
The electric field is along the x-axis. So, while calculating the potential difference between points B and A using the formula VB − VA = E.ds, we will use the difference of the x-coordinates of these point as ds.
(a) A = (0, 0) B = (4 m, 2 m).
So, VB − VA = E.ds = 20 × (0 − 4 m) = − 80 V
(b) A = (4 m, 2 m), B = (6 m, 5 m)
⇒ VB − VA = E.ds = 20 × (4 − 6) = − 40 V.
(c) A = (0, 0), B = (6 m, 5 m)
⇒ VB − VA = E.ds = 20 × (0 − 6) = − 120 V.
Potential difference between points (0, 0) and (6 m, 5 m) = Potential difference between points (0, 0) and (4 m, 2 m) + Potential difference between points (4 m, 2 m) and (6 m, 5 m)
Q.57. Consider the situation of the previous problem. A charge of −2.0 × 10−4 C is moved from point A to point B. Find the change in electrical potential energy UB − UA for the cases (a), (b) and (c).
Given:
Magnitude of charge, q = −2.0 × 10−4 C
(a) The electric field is along the x direction.
Thus, potential difference between (0, 0) and (4, 2),
dV = −E.dx = −20 × 4 = −80 V
Potential energy (UB − UA) between the points = dV × q
⇒ UB − UA = (−80) × (−2.0 × 10−4)
⇒ UB − UA = 160 × 10−4 = 0.016 J
(b) A = (4 m, 2m), B = (6 m, 5 m)
dV = −E.dx = − 20 × 2 = −40 V
Potential energy (UB − UA) between the points = dV × q
⇒ UB − UA = (−40) × (−2 × 10−4)
⇒ UB − UA = 80 × 10−4 = 0.008 J
(c) A = (0, 0) B = (6m, 5m)
dV = −E.dx = −20 × 6 = −120 V
Potential energy (UB − UA) between the points A and B = dV × q
⇒ UB − UA = (−120) × (−2 × 10−4)
⇒ UB − UA = 240 × 10−4 = 0.024 J
Q.58. An electric field 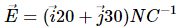 exists in space. If the potential at the origin is taken to be zero, find the potential at (2 m, 2 m).
exists in space. If the potential at the origin is taken to be zero, find the potential at (2 m, 2 m).
Given:
Q.59. An electric field 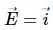 Ax exists in space, where A = 10 V m−2. Take the potential at (10 m, 20 m) to be zero. Find the potential at the origin.
Ax exists in space, where A = 10 V m−2. Take the potential at (10 m, 20 m) to be zero. Find the potential at the origin.
Given:
Electric field intensity,
So, at the origin, the potential is 500 V.
Q.60. The electric potential existing in space is 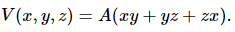 (a) Write the dimensional formula of A. (b) Find the expression for the electric field. (c) If A is 10 SI units, find the magnitude of the electric field at (1 m, 1 m, 1 m).
(a) Write the dimensional formula of A. (b) Find the expression for the electric field. (c) If A is 10 SI units, find the magnitude of the electric field at (1 m, 1 m, 1 m).
Given:
Electric potential,
(b) Let E be the electric field.
Equating now, we get
Magnitude of electric field,
Q.61. Two charged particles, with equal charges of 2.0 × 10−5 C, are brought from infinity to within a separation of 10 cm. Find the increase in the electric potential energy during the process
Magnitude of charges, q1 = q2 = 2 × 10−5 C
Initial potential energy = 0
Each is brought from infinity to within a separation of 10 cm.
That is, r = 10 × 10−2 m
So, increase in potential energy = final potential energy − initial potential energy.
That is, increase in potential energy,
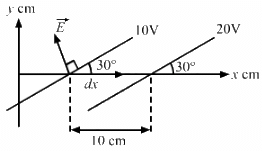
Q.62. Some equipotential surface is shown in the figure. What can you say about the magnitude and the direction of the electric field?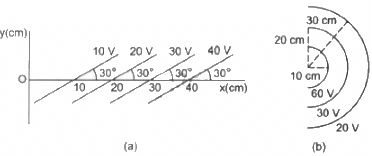
(a) The electric field is always perpendicular to the equipotential surface. (As shown in the figure)
So, the angle between
Change in potential in the first and second equipotential surfaces, dV = 10 V
so,
The electric field is making an angle of 120° with the x axis.
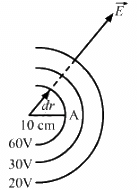
(b) The electric field is always perpendicular to the equipotential surface.
So, the angle between
Potential at point A,
The electric field is radially outward, decreasing with increasing distance.
Q.63. Consider a circular ring of radius r, uniformly charged with linear charge density λ. Find the electric potential at a point on the axis at a distance x from the centre of the ring. Using this expression for the potential, find the electric field at this point.
Given:
Radius of the ring = r
So, circumference = 2πr
Charge density = λ,
Total charge, q = 2πr × λ
Distance of the point from the centre of the ring = x
Distance of the point from the surface of the ring,
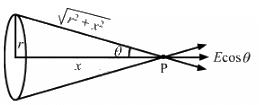
Due to symmetry at point P, vertical component of electric field vanishes.
So, net electric field = Ecosθ
Q.64. An electric field of magnitude 1000 NC−1 is produced between two parallel plates with a separation of 2.0 cm, as shown in the figure. (a) What is the potential difference between the plates? (b) With what minimum speed should an electron be projected from the lower place in the direction of the field, so that it may reach the upper plate? (c) Suppose the electron is projected from the lower place with the speed calculated in part (b). The direction of projection makes an angle of 60° with the field. Find the maximum height reached by the electron.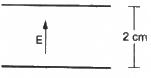
Given :
Electric field intensity, E = 1000 N/C
Separation between the plates, l = 2 cm = 0.02 m
(a) The potential difference between the plates,
(b) The acceleration of an electron,
(c) Now, u = ucos60° Final velocity, v = 0
Let the maximum height reached be s.
Q.65. A uniform field of 2.0 NC−1 exists in space in the x-direction. (a) Taking the potential at the origin to be zero, write an expression for the potential at a general point (x, y, z). (b) At which point, the potential is 25 V? (c) If the potential at the origin is taken to be 100 V, what will be the expression for the potential at a general point? (d) What will be the potential at the origin if the potential at infinity is taken to be zero? Is it practical to choose the potential at infinity to be zero?
(a) Given:
Electric field intensity, E = 2 N/C in the x-direction
(a) Potential at the origin = 0
(b) From the above expression for V, we have
(c) If potential at the origin is 100 V, then potential at a general point is given by
(d) Potential at infinity is given by V' - V = -2x,
where V is the potential at the origin.
It is not practical to take the potential at infinity to be zero because in that case, we have to take the potential at origin to be infinity and the calculations will become practically impossible.
Q.66. How much work has to be done in assembling three charged particles at the vertices of an equilateral triangle, as shown in the figure?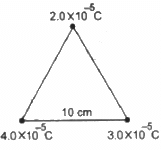
Let
Side of the equilateral triangle = l
As
Work done in assembling the charges = Net potential energy of the system
Q.67. The kinetic energy of a charged particle decreases by 10 J as it moves from a point at potential 100 V to a point at potential 200 V. Find the charge on the particle.
By work-energy theorem,
Change in K.E. = Amount of work done
Change in K.E. = 10 J
Let the charge on the particle be q.
Change in potential,
Q.68. Two identical particles, each with a charge of 2.0 × 10−4 C and mass of 10 g, are kept at a separation of 10 cm and then released. What would be the speed of the particles when the separation becomes large?
Given:
Magnitude of charges, q = 2.0 × 10−4 C
Mass of particles, m = 10 g = 0.01 kg
Separation between the charges, r = 10 cm = 0.1 m
Force of repulsion,
Now,
Q.69. Two particles of masses 5.0 g each and opposite charges of +4.0 × 10−5 C and −4.0 × 10−5 C are released from rest with a separation of 1.0 m between them. Find the speeds of the particles when the separation is reduced to 50 cm.
Given:
Magnitude of charges, q = 4.0 × 10−5 C
Initial separation between charges, r = 1 m
Initial speed = 0; so, initial K.E. = 0
Mass of the particles, m = 5.0 g =0.005 kg
Let the required velocity of each particle be v.
By the law of conservation of energy,
Initial P.E. + Initial K.E. = Final P.E. + Final K.E.
Q.70. A sample of HCI gas is placed in an electric field of 2.5 × 104 NC−1. The dipole moment of each HCI molecule is 3.4 × 10−30 Cm. Find the maximum torque that can act on a molecule.
Given:
Electric field intensity, E = 2.5 × 104 NC−1
Dipole moment of an HCl molecule, P = 3.4 × 10−30 Cm
Torque on the molecule,
Q.71.1. Two particles A and B, of opposite charges 2.0 × 10−6 C and −2.0 × 10−6 C, are placed at a separation of 1.0 cm. Two particles A and B, of opposite charges 2.0 × 10−6 C and −2.0 × 10−6 C, are placed at a separation of 1.0 cm.
Given:
Magnitude of charge, q = 2.0 × 10−6 C
Separation between the charges, l = 1.0 cm
Dipole moment, P = q × l
Q.71.2. Two particles A and B, of opposite charges 2.0 × 10−6 C and −2.0 × 10−6 C, are placed at a separation of 1.0 cm. Calculate the electric field at a point on the axis of the dipole 1.0 cm away from the centre.
Given:
Magnitude of charge, q = 2.0 × 10−6 C
Separation between the charges, l = 1.0 cm
Electric field at the axial point of the dipole,
E = 36 × 107 N/C
Q.71.3. Two particles A and B, of opposite charges 2.0 × 10−6 C and −2.0 × 10−6 C, are placed at a separation of 1.0 cm. Calculate the electric field at a point on the perpendicular bisector of the dipole and 1.0 m away from the centre.
Given:
Magnitude of charge, q = 2.0 × 10−6 C
Separation between the charges, l = 1.0 cm
Electric field at at a point on the perpendicular bisector of the dipole,
E = 180 N/C
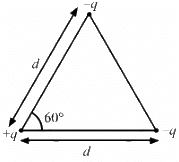
Q.72. Three charges are arranged on the vertices of an equilateral triangle, as shown in the figure. Find the dipole moment of the combination.
The system can be considered as a combination of two dipoles making an angle of 60∘ with each other.
Length of each dipole = d
So, the dipole moment, P = q × d
So, the resultant dipole moment,
The net dipole moment is along the bisector of the angle at +q, away from the triangle.
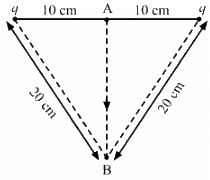
Q.73. Find the magnitude of the electric field at the point P in the configuration shown in the figure for d >> a.
Taking
Q.74. Two particles, carrying charges −q and +q and and of mass m each, are fixed at the ends of a light rod of length a to form a dipole. The rod is clamped at an end and is placed in a uniform electric field E with the axis of the dipole along the electric field. The rod is slightly tilted and then released. Neglecting gravity, find the time period of small oscillations.
Consider the rod to be a simple pendulum
Time period of a simple pendulum,
(where l = length and a' = acceleration)
Now
Q.75. Assume that each atom in a copper wire contributes one free electron. Estimate the number of free electrons in a copper wire of mass 6.4 g (take the atomic weight of copper to be 64 g mol−1).
Atomic weight of copper = 64 grams
No. of moles in 64 g of copper = 1
∴ No. of moles in 6.4 g of copper = 0.1
No. of atoms in 1 mole of copper = 6 × 10−23 = Avogadro's Number
No. of atoms in 0.1 mole = (6 × 10−23 × 0.1) = 6 × 1022
1 atom contributes 1 free electron.
∴ 6 × 1022 atoms contribute 6 × 1022 free electrons.
|
134 docs
|
FAQs on HC Verma Questions and Solutions: Chapter 29: Electric Field & Potential- 3 - HC Verma Solutions - JEE
| 1. What is the electric field? |  |
| 2. How is electric field strength measured? |  |
| 3. What is the difference between electric field and electric potential? |  |
| 4. How is the electric field calculated due to a point charge? |  |
| 5. What is the relationship between electric field and electric potential energy? |  |