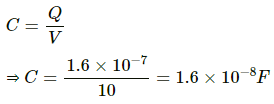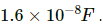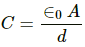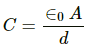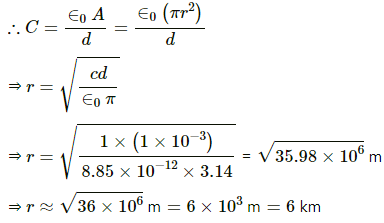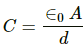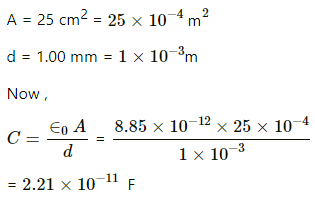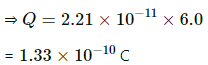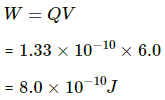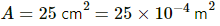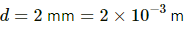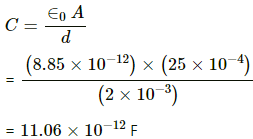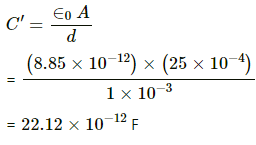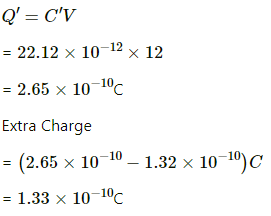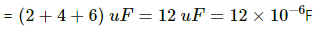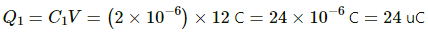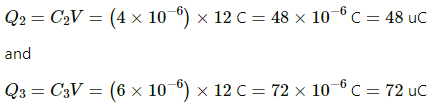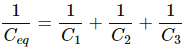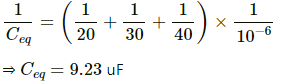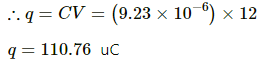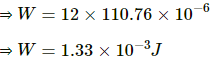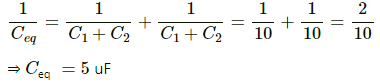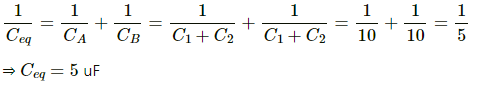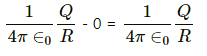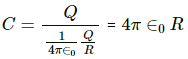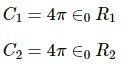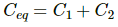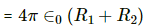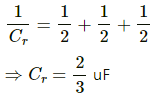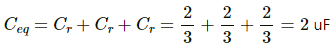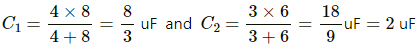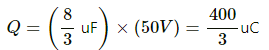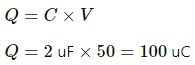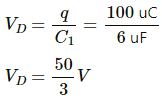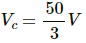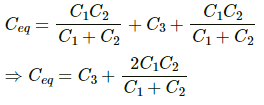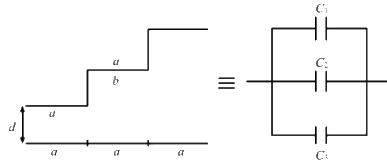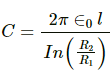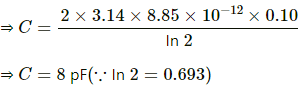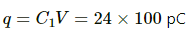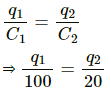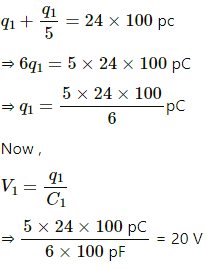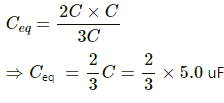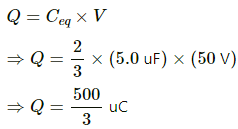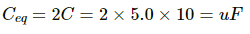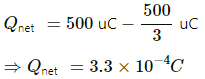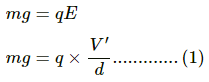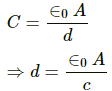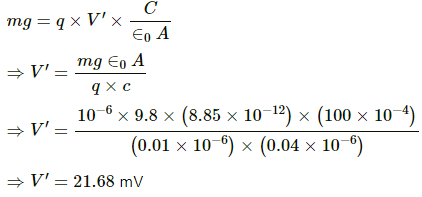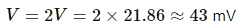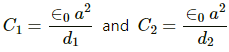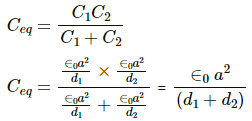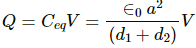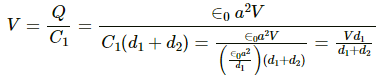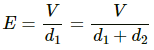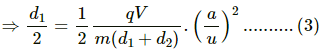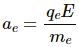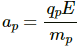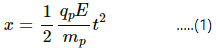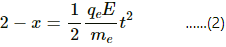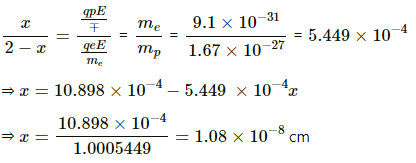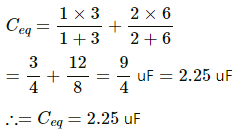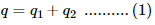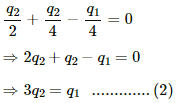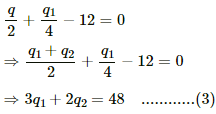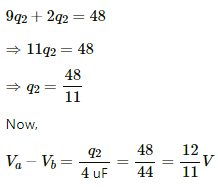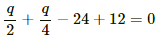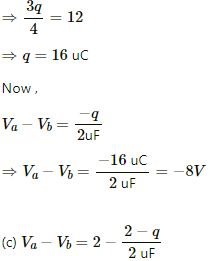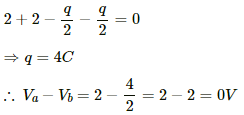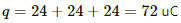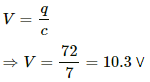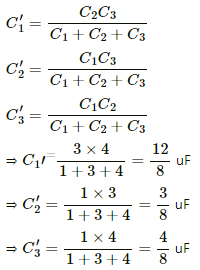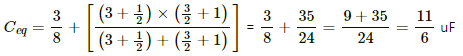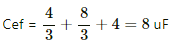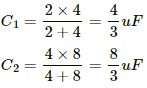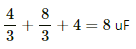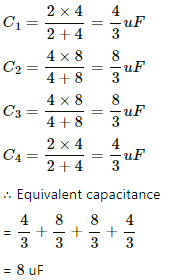HC Verma Questions and Solutions: Chapter 31: Capacitors- 2 | HC Verma Solutions - JEE PDF Download
Exercises
Q.1. When 1⋅0 × 1012 electrons are transferred from one conductor to another, a potential difference of 10 V appears between the conductors. Calculate the capacitance of the two-conductor system.
As 1.0 × 1012 electrons are transferred from one conductor to another, the conductor to which the electrons are transferred becomes negatively charged and the other conductor becomes positively charged.
Now,
Magnitude of the net charge on each conductor,
Magnitude of the potential difference between the conductors, V = 10 V
The capacitance C is the ratio of the magnitude of the charge on either conductor to the magnitude of the potential difference between the conductors.
Hence, the value of the capacitance of the given two conductor systems is
Q.2. The plates of a parallel-plate capacitor are made of circular discs of radii 5⋅0 cm each. If the separation between the plates is 1⋅0 mm, what is the capacitance?
The capacitance of a parallel-plate capacitor is given by
Here,
A = Area of the plate
d = Distance between the parallel plates
Given :
Q.3. Suppose, one wishes to construct a 1⋅0 farad capacitor using circular discs. If the separation between the discs be kept at 1⋅0 mm, what would be the radius of the discs?
The capacitance of a parallel-plate capacitor is given by
Here,
A = Area of the plate
d = Distance between the parallel plates
Now,
Let the radius of the disc be r.
Thus, the radius of the plates of the capacitor for the given configuration is 6 km.
Q.4. A parallel-plate capacitor having plate area 25 cm2 and separation 1⋅00 mm is connected to a battery of 6⋅0 V. Calculate the charge flown through the battery. How much work has been done by the battery during the process?
The capacitance of a parallel-plate capacitor is given by
Here,
A = Area of the plate
d = Distance between the parallel plates
Given :
When the battery of voltage 6 V is connected to the capacitor, the charge (Q) that flows from the battery is equal to the amount of the charge that the given capacitor can hold.
⇒ Q = CV
The work done by the battery in charging the capacitor is calculated by taking the product of the magnitude of the charge transferred and the voltage of the battery.
Thus, we get
Thus , the charge flown through the battery is 1.33 x 10-10C and the work done by the battery is 8.0 x 10-10J.
Q.5. A parallel-plate capacitor has plate area 25⋅0 cm2 and a separation of 2⋅00 mm between the plates. The capacitor is connected to a battery of 12⋅0 V. (a) Find the charge on the capacitor. (b) The plate separation is decreased to 1⋅00 mm. Find the extra charge given by the battery to the positive plate.
Given :
Area of the plate,
Separation between the plates,
Potential difference between the plates, V = 12 V
The capacitance of the given capacitor is given by
(a) Charge on the capacitor is given by
Q = CV
(b) When the separation between the plates is decreased to 1 mm , the capacitance C' can be calculated as :
Charge on the capacitor is given by
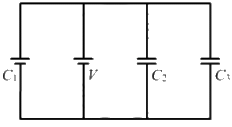
Q.6. Find the charges on the three capacitors connected to a battery as shown in figure.
Take 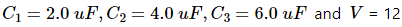 volts.
volts.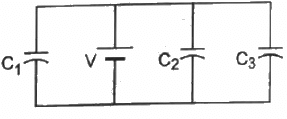
The capacitances of three capacitors are C1= 2 μF, C2= 4 μF and C3= 6 μF and the voltage of the battery (V) is 12 V.
As the capacitors are connected in parallel, the equivalent capacitance is given by
Ceq = C1 + C2 + C3
Due to parallel connection, the potential difference across each capacitor is the same and is equal to 12 V.
Therefore, the charge on each capacitor can be calculated as follows :
The charge on the capacitor of capacitance C1= 2 μF is given by
Similarly, the charges on the other two capacitors are given by
Q.7. Three capacitors having capacitances 20 µF, 30 µF and 40 µF are connected in series with a 12 V battery. Find the charge on each of the capacitors. How much work has been done by the battery in charging the capacitors?
When the capacitors are connected in series, the equivalent capacitance is given by
Because the capacitors are connected in series, the same charge will go to each of them and it is equal to the total charge given by the battery.
Now,
Let the charge at each capacitor be q.
The Work done by the battery (W) is given by
W = qV
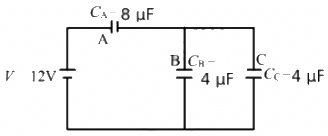
Q.8. Find the charge appearing on each of the three capacitors shown in figure .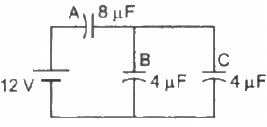
Let us first find the equivalent capacitance. It can be observed from the circuit diagram that capacitors B and C are in parallel and are in series with capacitor A.
The equivalent capacitance can be calculated as follow :-
Capacitors B and C are parallel and are in series with capacitor A. The equivalent capacitance of capacitors B and C is given by
(4 + 4) μF = 8 μF
It is the same as the capacitance of capacitor A. Therefore, equal potential difference will be there on capacitor A and the system of capacitors B and C.
Now,
Potential difference across capacitor A = 6 V
Thus,
Charge on capacitor A = (8 µF) × (6 V) = 48 µC
And,
Potential difference across capacitors B and C = 6 V
Charge on capacitor B = (4 µF) × (6 V) = 24 µF
Charge on capacitor C = (4 µF) × (6 V) = 24 µF
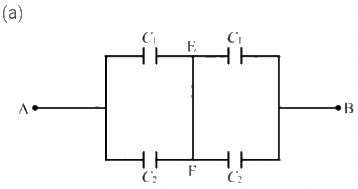
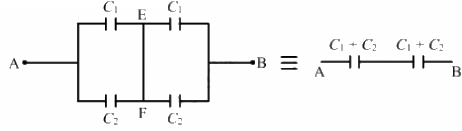
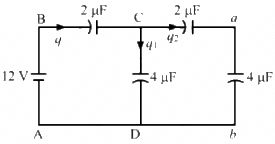
Q.9. Take 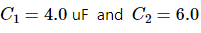 uF in figure . Calculate the equivalent capacitance of the combination between the points indicated.
uF in figure . Calculate the equivalent capacitance of the combination between the points indicated.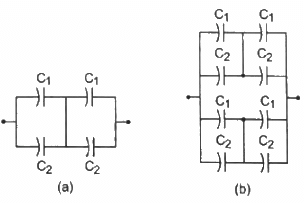
For the combination of capacitors given in figure (a), the pairs of capacitors C1 and C2 are in parallel.
The equivalent capacitance of each parallel combination of capacitors is given by C1 + C2 = 4 + 6 = 10 μF
The equivalent circuit can be drawn as :
The equivalent capacitance for the above series circuit is given by
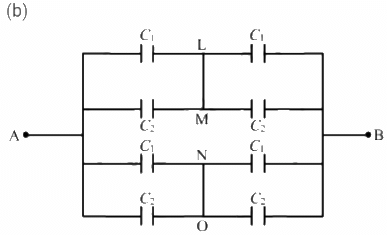
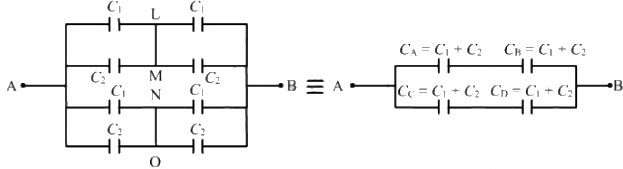
For the combination of capacitors given in figure (b), the pairs of capacitors C1 and C2 are in parallel.
The equivalent capacitance of each parallel combination of capacitors is given by
C1 + C2 = 4 + 6 = 10 μF
The equivalent circuit can be drawn as :
In the above circuit, it can be seen that CA and CB are in series and are in parallel to the series combination of CC and CB.
The equivalent capacitance for the series combination of CA and CB is given by
Similarly, the equivalent capacitance of the series combination of CC and CD is 5 μF.
∴ Net equivalent capacitance = 5 + 5 = 10 μF
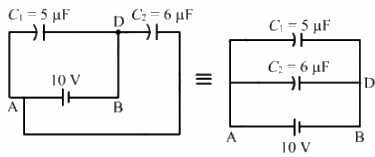
Q.10. Find the charge supplied by the battery in the arrangement shown in figure.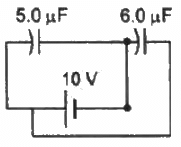
The equivalent circuit for the given case can be drawn as :-
It can be observed that capacitors C1 and C2 are in parallel.
Therefore, the equivalent capacitance is given by
Ceq = C1 + C2
= 5 + 6 = 11 μF
Now,
Charge supplied by the battery = (Ceq)(V) = (11 μF) × (10 V) = 110 μC
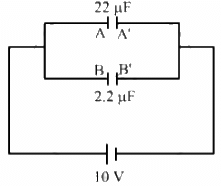
Q.11. The outer cylinders of two cylindrical capacitors of capacitance 2⋅2 µF each, are kept in contact and the inner cylinders are connected through a wire. A battery of emf 10 V is connected as shown in figure . Find the total charge supplied by the battery to the inner cylinders.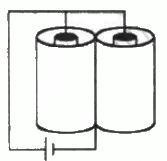
It is given that the outer cylinders are kept in contact and the inner cylinders are connected through a wire. Thus, the equivalent circuit can be drawn as :
The left plate of the capacitors (A and B) shown in the figure represents the inner plates of the cylindrical capacitors.
As the capacitors are connected in parallel, the potential difference across them is the same.
∴ Magnitude of the charge on each capacitor = CV = (2.2 μF) × (10V) = 22 µC
As plates A and B are connected to the positive terminal of the battery, the charge on each of them is +22 µC.
∴ Net charge on the inner plates = 22 µC + 22 µC = +44 µC
Q.12. Two conducting spheres of radii R1 and R2 are kept widely separated from each other. What are their individual capacitances? If the spheres are connected by a metal wire, what will be the capacitance of the combination? Think in terms of series−parallel connections.
We need to calculate the capacitance of an isolated charged sphere.
Let us assume that the charge on the sphere is Q and its radius is R.
Capacitance of the charged sphere can be found by imagining a concentric sphere of infinite radius consisting of −Q charge.
Potential difference between the spheres =
Capacitance is the ratio of the magnitude of the charge on each conductor to the potential difference between them.
Therefore, the capacitances of spheres of radii R1 and R2 are C1 and C2, respectively. They are given by
If the spheres are connected by a metal wire, the charge will flow from one sphere to another till their potentials become the same.
As there potentials become the same, the potential difference between the conductors for both the capacitors also becomes the same. Thus, it can be concluded that the capacitors are connected in parallel.
Thus, the capacitance of the combination is given by
Q.13. Each of the capacitors shown in figure has a capacitance of 2 µF. find the equivalent capacitance of the assembly between the points A and B. Suppose, a battery of emf 60 volts is connected between A and B. Find the potential difference appearing on the individual capacitors.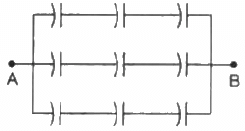
There are three rows of capacitors connected in parallel in the given system. In each row, three capacitors of capacitance 2 μF are connected in series.
For each row, the equivalent capacitance is given by
As three rows are connected in parallel, their equivalent capacitance is given by
The voltage across each row is the same and is equal to 60 V.
As all capacitors have the same capacitance in each row, the potential difference across their plates is the same.
∴ Potential difference across each capacitor = 20 V
Q.14. It is required to construct a 10 µF capacitor which can be connected across a 200 V battery. Capacitors of capacitance 10 µF are available but they can withstand only 50 V. Design a combination which can yield the desired result.
Let the number of capacitors in series (connected in a row) be x.
The maximum voltage that the capacitors can withstand is 50 V.
The voltage across each row should be equal to 200 V.
Therefore,
x × 50 = 200
Thus,
x = 4 capacitors
Now,
Let there be y such rows.
So, the equivalent capacitance of the combination will be xy.
⇒ xy = 10
⇒ y = 10 x = 4 capacitors
Thus, to yield the required result, the combination of 4 rows, each of 4 capacitors having capacitance 10 µF and breakdown voltage 50 V, is required.
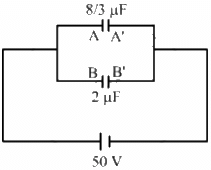
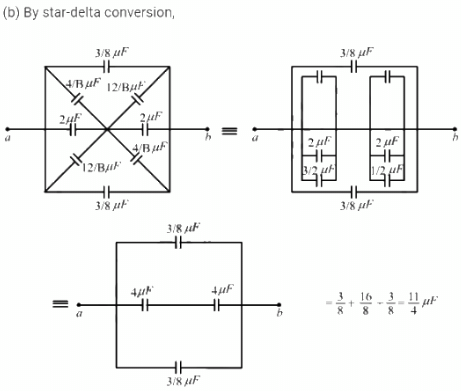
Q.15. Take the potential of the point B in figure to be zero. (a) Find the potentials at the points C and D. (b) If a capacitor is connected between C and D, what charge will appear on this capacitor?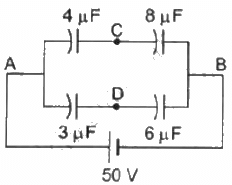
(a) The capacitance of the two rows connected in parallel is given by
As the two rows are in parallel, the potential difference across each row is the same and is equal to 50 V.
The charge on the branch ACB with capacitance 8/3 uf is given by
The charge on the branch ADB with capacitance 2uF is given by
The potential at point D is given by
Similarly, the potential at point C is given by
(b) As the potential difference between points C and D is zero, the bridge remains balanced and no charge flows from C to D. If a capacitor is connected between points C and D, then the change on the capacitor will be zero.
Q.16. Find the equivalent capacitance of the system shown in figure between the points a and b.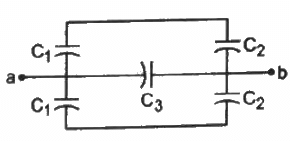
Capacitors C1 and C2 above and below ab are connected in series and in parallel with C3.
Thus, the equivalent capacitor between a and b is given by
Q.17. A capacitor is made of a flat plate of area A and a second plate having a stair-like structure as shown in figure . The width of each stair is a and the height is b. Find the capacitance of the assembly.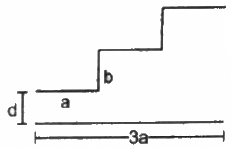
The total area of the flat plate is A. The width of each stair is the same. Therefore, the area of the surface of each stair facing the flat plate is the same, that is, A/3.
From the figure, it can be observed that the capacitor assembly is made up of three capacitors. The three capacitors are connected in parallel.
For capacitor C1, the area of the plates is A/3 and the separation between the plates is d.
For capacitor C2, the area of the plates is A/3 and the separation between the plates is (d + b).
For capacitor C3, the area of the plates is A/3 and the separation between the plates is (d + 2b).
Therefore,
As the three capacitors are in parallel combination,
Q.18. A cylindrical capacitor is constructed using two coaxial cylinders of the same length 10 cm and of radii 2 mm and 4 mm. (a) Calculate the capacitance. (b) Another capacitor of the same length is constructed with cylinders of radii 4 mm and 8 mm. Calculate the capacitance.
(a) The capacitance of a cylindrical capacitor is given by
(b) When a capacitor of the same height with cylinders of radii 4 mm and 8 mm is taken, its capacitance comes to 8 pF, which is the same as above because the ratio of the radii is the same.
Q.19. A 100 pF capacitor is charged to a potential difference of 24 V. It is connected to an uncharged capacitor of capacitance 20 pF. What will be the new potential difference across the 100 pF capacitor?
Given :
C1 = 100 pF
V = 24 V
Charge on the capacitor
Capacitance of the uncharged capacitor, C2 = 20 pF
When the charged capacitor is connected with the uncharged capacitor, the net charge on the system of the capacitors becomes....(i)
The potential difference across the plates of the capacitors will be the same.
Thus,......(ii)
From eqs. (i) and (ii), we get
Q.20. Each capacitor shown in figure has a capacitance of 5⋅0 µF. The emf of the battery is 50 V. How much charge will flow through AB if the switch S is closed?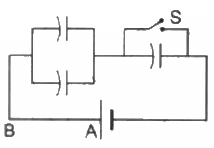
Initially, when the switch S is open, the equivalent capacitance is given by
The Charge supplied by the battery is given by
When the switch S is closed, no charge goes to the capacitor connected in parallel with the switch.
Thus, the equivalent capacitance is given by
The charge supplied by the battery is given by
The initial charge stored in the shorted capacitor starts discharging."?
Hence, the charge that flows from A to B is given by
Q.21. The particle P shown in figure has a mass of 10 mg and a charge of −0⋅01 µC. Each plate has a surface area 100 cm2 on one side. What potential difference V should be applied to the combination to hold the particle P in equilibrium?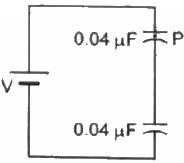
The particle is balanced when the electrical force on it is balanced by its weight.
Thus,
Here,
d = Separation between the plates of the capacitor
V' = Potential difference across the capacitor containing the particle
We know that the capacitance of a capacitor is given by
Thus, eq. (1) becomes
Since the values of both the capacitors are the same,
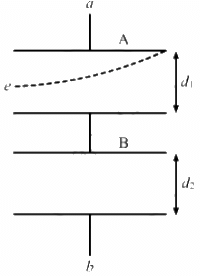
Q.22. Both the capacitors shown in figure are made of square plates of edge a. The separations between the plates of the capacitors are d1 and d2 as shown in the figure. A potential difference V is applied between the points a and b. An electron is projected between the plates of the upper capacitor along the central line. With what minimum speed should the electron be projected so that it does not collide with any plate? Consider only the electric forces.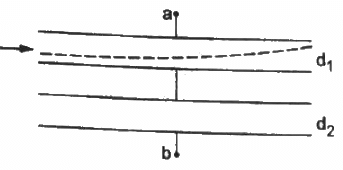
Let
Velocity of the electron = u
Mass of the electron = m
Now,
Horizontal distance, x = u × t
Let the electric field inside the capacitor be E
∴ Acceleration of the electron = qE/m
Vertical Distance,
Capacitance of the two capacitors :-
It is given that the capacitors are connected in series.
Thus, the equivalent capacitance is given by
Total charge on the system of capacitors,
As the capacitors are in series, charge on both of them is the same.
The potential difference across the capacitor containing the electron is given by
The magnitude of the electric field inside the capacitor is given by
The charge on electron q is represented by e.
On putting the values of q and E in (2), we get
The minimum velocity of the electron is given by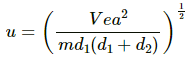
Q.23. The plates of a capacitor are 2⋅00 cm apart. An electron-proton pair is released somewhere in the gap between the plates and it is found that the proton reaches the negative plate at the same time as the electron reaches the positive plate. At what distance from the negative plate was the pair released?
Let the electric field inside the capacitor be E.
Now ,
Magnitude of acceleration of the electron,
Magnitude of acceleration of the proton,
Let t be the time taken by the electron and proton to reach the positive and negative plates, respectively.
The initial velocities of the proton and electron are zero.
Thus, the distance travelled by the proton is given by
And, the distance travelled by the electron is given by
On dividing (1) by (2), we get
Q.24. Convince yourself that parts (a), (b) and (c) figure are identical. Find the capacitance between the points A and B of the assembly.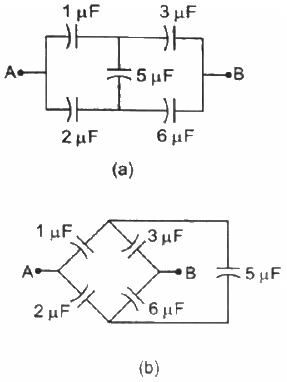
Parts (a), (b) and (c) are identical, as all of them form a bridge circuit. In that circuit, capacitors of 1 µF and 2 µF are connected to terminal A and the 5 µF capacitor and capacitors of 3 µF and 6 µF are connected to terminal B and the 5 µF capacitor.
For the given situation, it can be observed that the bridge is in balance; thus, no current will flow through the 5 µF capacitor.
So to simplify the circuit, 5 µF capacitor can be removed from the circuit.
Now, 1 µF and 3 µF capacitors are in series.
And 2 µF and 6 µF capacitors are also in series combination.
These two combination are in parallel with each other.
The equivalent capacitance can be calculated as :-
Thus , parts (a) , (b) and (c) are identical.
And,
Ceq = 2.25 uF
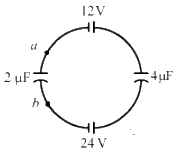
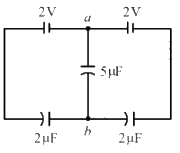
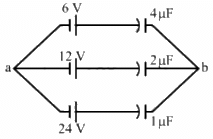
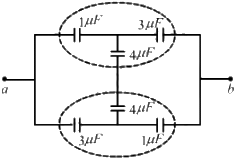
Q.25. Find the potential difference Va - Vb between the points a and b shown in each part of the figure.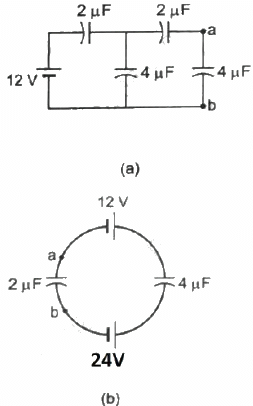
(a)
On applying Kirchhoff's voltage law in the loop CabDC, we get
On applying Kirchhoff's voltage law in the loop DCBAD, we get
From eqs. (2) and (3), we get
(b) Let the charge in the loop be q.
Now, on applying Kirchhoff's voltage law in the loop, we get
In the loop,
Net Charge flowing through all branches,
Net capacitance of all branches, C = 4 + 2 + 1 = 7 μF
The Total potential difference (V) between points a and b is given by
As the negative terminals of the batteries are connected to a, the net potential between points a and b is -10.3 V .
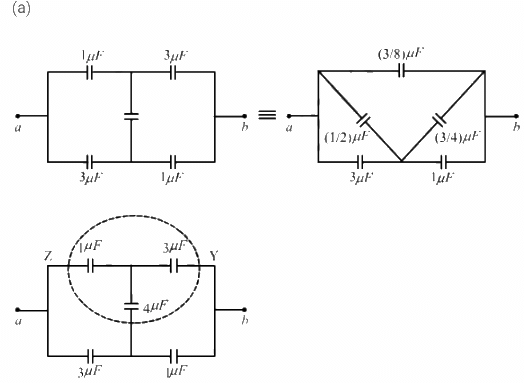
Q.26. Find the equivalent capacitances of the combinations shown in figure between the indicated points.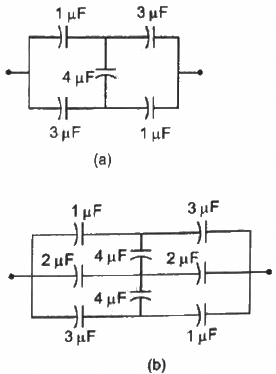

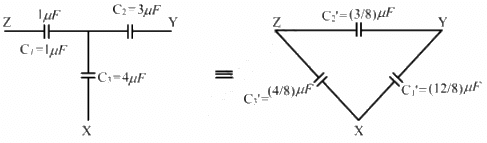
Applying star-delta conversion in the part indicated in the diagram.
The Capacitance of the C1 is given by
Thus, the equivalent circuit can be drawn as :
Therefore, the equivalent capacitance is given by
1 + 1 = 2 uF
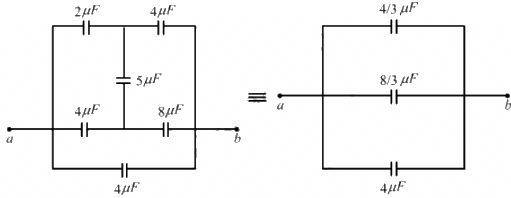
(c) It is a balanced bridge.
Therefore, the capacitor of capacitance 5 μF can be removed.
The capacitance of the two branches are :
∴ Equivalent capacitance =
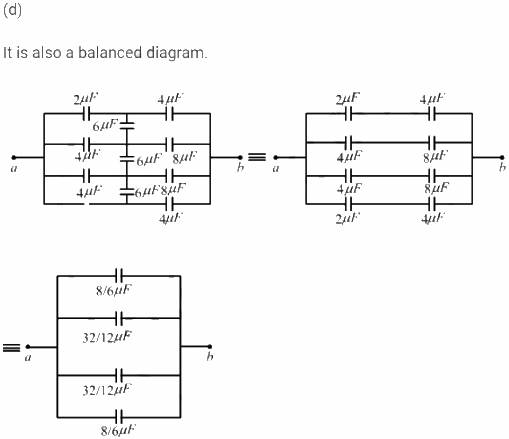
It can be observed that the bridges are balanced.
Therefore, the capacitors of capacitance 6 μF between the branches can be removed
The capacitances of the four branches are :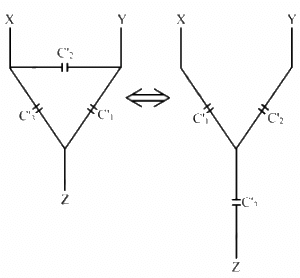
|
134 docs
|