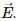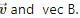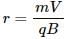Short Answers
Q.1. Suppose a charged particle moves with a velocity v near a wire carrying an electric current. So, a magnetic force acts on it. If the same particle is seen from a frame moving with velocity v in the same direction, the charge will be found to be at rest. Will the magnetic force become zero in this frame? Will the magnetic field become zero in this frame?
Magnetic force becomes zero as the particle is at rest in this frame of reference and we know that force on a particle,
F = qvBsin(θ">θθ), where v is the velocity of the particle.
So, when v = 0, F = 0.
Magnetic field on the particles still exists because the current is independent of the frame of reference. For any reason, if the electrons of the wire seem to be at rest in a frame of reference, the protons are still flowing opposite to the frame of reference. Due to this, the current and the magnetic fields still exist.
Q.2. Can a charged particle be accelerated by a magnetic field? Can its speed be increased?
Yes, a charged particle can be accelerated by a magnetic field. A magnetic field exerts force on the charged particle, which is perpendicular to both the magnetic field and velocity. If initially the charged particle is moving at right angle to the magnetic field, then the resultant trajectory of the particle is circular motion. In circular motion, the magnitude of the velocity remains constant but direction changes continuously. So, the motion is accelerated but speed remains constant.
Q.3. Will a current loop placed in a magnetic field always experience a zero force?
No, it depend on the magnetic field, i.e. whether the field is a uniform or a non-uniform magnetic field and also on the orientation of the current loop. In case of a uniform magnetic field, the force on the circular loop is zero if the magnetic field is parallel to the plane of the loop and in case of a non-uniform magnetic field, the force may or may not be zero.
Q.4. The free electrons in a conducting wire are in constant thermal motion. If such a wire, carrying no current, is placed in a magnetic field, is there a magnetic force on each free electron? Is there a magnetic force on the wire?
As the electrons are in motion, there is a magnetic force acting on them individually. But the current through the wire represents the collective motion of all the electrons that are moving or vibrating very randomly; so, overall effect is negligible. Hence there is no net magnetic force on the wire.
Also, F = LLB sin (θ)
So, if the current in the wire is zero, then the force experienced by the wire will also be zero.
Q.5. Assume that the magnetic field is uniform in a cubical region and zero outside. Can you project a charged particle from outside into the field, so that the particle describes a complete circle in the field?
Let us assume that the magnetic field is uniform and is acting along positive x axis in the cubical region.
Now if we project a charged particle inside this cube along positive y axis then as the direction of velocity and magnetic field is perpendicular to each other so the resultant trajectory of the particle will be a circle.
Q.6. An electron beam projected along the positive x-axis deflects along the positive y-axis. If this deflection is caused by a magnetic field, what is the direction of the field? Can we conclude that the field is parallel to the z-axis?
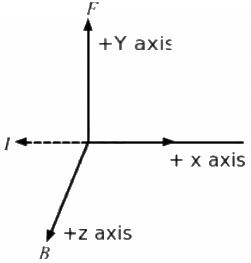
As the particle gets deflected towards the positive y-axis, we can conclude that force is acting on the particle along the positive y-axis. Now, as the electron is moving along the positive x-axis, the current can be assumed to be flowing along the negative x-axis. Applying Fleming's left-hand rule, we find that the thumb points in the direction of force, i.e. the positive y-axis and the middle finger points in the direction of current, i.e. negative x-axis. Consequently, the forefinger gives us the direction of magnetic field, i.e. out of the plane of the paper or in the positive z-direction. So, we can conclude that the magnetic field is pointing along the positive z-axis.
Q.7. Is it possible for a current loop to stay without rotating in a uniform magnetic field? If yes, what should be the orientation of the loop?
Yes, if the direction of the area vector coincides with the direction of the magnetic field, the torque acting on the loop due to the magnetic field will become zero. Hence, no rotation will be produced in the coil.
It follows from the fact that torque acting on the loop is directly proportional to si θθ, where θθ is the angle made by the area vector with the direction of the magnetic field. So, we can see from this correlation that torque is zero if
θ = 0 or θ = 180°.
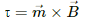
= mBsin (θ)
⇒ For θ = 0 or integral multiple of π ,
τ = 0
Which implies that the coil will not rotate.
Q.8. The net charge in a current-carrying wire is zero. Then, why does a magnetic field exert a force on it?
The net charge in a current- carrying wire is zero. Yet, negative charge, i.e. electrons are moving in the wire towards the positive terminal. It is this motion of electrons in the conductor which produces the current in the wire and is also responsible for the magnetic force acting on the wire.
F = qVBsin(θθ), where F is the force, q is the charge of electrons, V is the velocity of electrons and B is the magnetic field.
Moreover, the positive charges on the wire are due to nucleus containing proton. As they are not moving so there is no force on them, so the force is only due to the moving electrons in the wire.
Q.9. The torque on a current loop is zero if the angle between the positive normal and the magnetic field is either θ = 0 or θ = 180°. In which of the two orientations, the equilibrium is stable?
If the angle between the positive normal and the magnetic field is 0, then the equilibrium is stable. It follows directly from the fact that U = - mBcos θ where m is the magnetic moment. So, when θ is 0, Potential energy, i.e. U of the system is negative, the system is more stable. But if θ is 180°, U is positive or the system is unstable.
Stability of a system depends on its energy and every system tries to minimise its energy. The configuration of the system with least energy is most stable and the configuration with the most energy is least stable or unstable.
Q.10. Verify that the units weber and volt second are the same.
Force experienced by the charge q moving with velocity v in a magnetic field B is given by
F = qVB
Hence, B = F/qV
Also, weber/m2 is the unit for magnetic field B.
Now, equating both the units of the magnetic field B, we get:
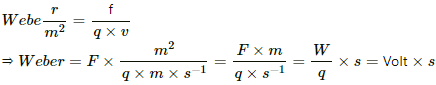
Thus, the units weber and volt second are same.
Multiple Choice Questions
Question for HC Verma Questions and Solutions: Chapter 34: Magnetic Field- 1
Try yourself:A positively-charged particle projected towards east is deflected towards north by a magnetic field. The field may be
Explanation
A positively-charged particle projected towards east can be considered as current in the eastern direction. Here, the positive charge is deflected towards the north by a magnetic field, i.e. the positively-charged particle experiences a force in the northern direction.
Hence, in order to determine the direction of the magnetic field, we apply Fleming's left-hand rule. According to this rule, when we stretch the thumb, the fore-finger and the middle finger mutually perpendicular to each other, then the thumb gives the direction of the force experienced by the charged particle, the fore-finger gives the direction of the magnetic field and the middle finger gives the direction of the current. Thus, if we direct the middle finger in the eastern direction, the thumb in the northern direction, we see that the fore-finger points in the downward direction.
Thus, the direction of the magnetic field is found to be in the downward direction.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 34: Magnetic Field- 1
Try yourself:A charged particle is whirled in a horizontal circle on a frictionless table by attaching it to a string fixed at one point. If a magnetic field is switched on in the vertical direction, the tension in the string
Explanation
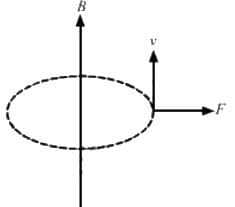
When the charged particle is whirled in a horizontal circle, at any moment, the current direction can be taken along the tangent of the circle. Also, the magnetic field is in the vertical direction. So, using Fleming's left-hand rule, the force can be radially outward or inward, depending on the direction of the magnetic field, i.e. either upward or downward. Also, the direction of force depends on the direction of the whirl, i.e. clockwise or anticlockwise and obviously on the charge of the particle, i.e. whether it is positive or negative. So, the correct answer is that the tension may increase or decrease.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 34: Magnetic Field- 1
Try yourself:Which of the following particles will experience maximum magnetic force (magnitude) when projected with the same velocity perpendicular to a magnetic field?
Explanation
Force on a moving charged particle,
F = qVBsin θ
As velocity V and magnetic field B are constant, and angle between the magnetic field and charged particle is 90° , the only thing on which force F depends is charge q.
Now, the charge on Li++ charge on electron, proton or He+ . So the force is maximum for Li++.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 34: Magnetic Field- 1
Try yourself:Which of the following particles will describe the smallest circle when projected with the same velocity perpendicular to a magnetic field?
Explanation
When a particle moves in a magnetic field, the necessary centripetal force, for the particle to move in a circle, is provided by the magnetic force acting on the particle.
So, equating the Lorentz force with the cetripetal force for a charged particle of charge q describing a circle of radius r, we get:
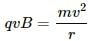
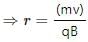
Here, m is the mass of the particle and v is its velocity.
The amount of charge of all the given particles is same; hence, for a given charge, r ∝ m . And since the electron is the lightest of all the particles, it describes the smallest circle when projected with the same velocity perpendicular to the magnetic field.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 34: Magnetic Field- 1
Try yourself:Which of the following particles will have minimum frequency of revolution when projected with the same velocity perpendicular to a magnetic field?
Explanation
Time period of the revolution of the particle, 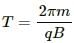
As frequency is the reciprocal of time period, so 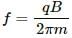
The charge on all the four particles is same. But the mass is maximum for Li+. So, it will have the smallest frequency of revolution.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 34: Magnetic Field- 1
Try yourself:A circular loop of area 1 cm2, carrying a current of 10 A, is placed in a magnetic field of 0.1 T perpendicular to the plane of the loop. The torque on the loop due to the magnetic field is
Explanation
When a circular loop is placed in a uniform magnetic field, it always experiences zero toque. We all know that a current-carrying wire experiences a force when placed in an external magnetic field. But in the case of a circular loop, forces are present in pairs, i.e. they are equal and opposite in magnitude. So, for every point on the loop, there exists another point on the diametrically opposite edge for which the force is equal and opposite to the force acting on first point. So, these two forces cancel in pair. In this way, the net torque on the loop is always zero when placed in a uniform magnetic field.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 34: Magnetic Field- 1
Try yourself:A beam consisting of protons and electrons moving at the same speed goes through a thin region in which there is a magnetic field perpendicular to the beam. The protons and the electrons
Explanation
Force on a charged particle, F = qVB
For an electron, this force is F = −-eVB, whereas on a proton this force is F = eVB.
Here, 'e' is the charge of the electron. So, from the above formulas, we can see that electrons and protons will experience equal force but in opposite directions; so they separate out. In other words, we can say that they are deviated by different angles and causes them to separate.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 34: Magnetic Field- 1
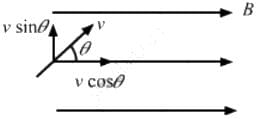
Try yourself:A charged particle moves in a uniform magnetic field. The velocity of the particle at some instant makes an acute angle with the magnetic field. The path of the particle will be
Explanation
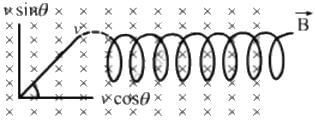
From the figure, the velocity of the particle can be resolved in two components,Vcosc parallel to the magnetic field and Vsin θ perpendicular to the magnetic field. We know that magnetic field does not change the speed of a particle; rather, it changes the direction of its velocity. So, a magnetic force acts on the particle due to the vertical component of velocity, which tries to move the particle in a circle.This force tries to rotate the particle in a circle. But as there is a horizontal component of velocity also, the particle will move helically with a constant pitch because no force acts on the particle along the direction of the horizontal component of velocity.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 34: Magnetic Field- 1
Try yourself:A particle moves in a region with a uniform magnetic field and a parallel, uniform electric field. At some instant, the velocity of the particle is perpendicular to the field direction. The path of the particle will be
Explanation
Here, the total Lorentz force on the particle,
F = qE + qVB
We all know that magnetic field B does not change the speed of the particle but changes its direction. But as an electric field is also present that accelerate the particle in the direction of the field, the resultant path is a helix with a non-uniform pitch.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 34: Magnetic Field- 1
Try yourself:An electric current i enters and leaves a uniform circular wire of radius a through diametrically opposite points. A charged particle q, moving along the axis of the circular wire, passes through its centre at speed v. The magnetic force acting on the particle, when it passes through the centre, has a magnitude equal to
Explanation
We can use the right-hand thumb rule to get the direction of magnetic field due to the current-carrying wire. Based on this, it can be determined that the direction of magnetic field is along the axis of the wire. Also, the charged particle is moving along the axis. So, no magnetic force will act on it, as the angle between the magnetic field and the velocity of the charged particle may be 0^° or 180 ° . So, sin θ of the angles between velocity and magnetic field is zero.
Also, the force, F=qVB sin θ
So, the force on the charged particle is zero.
Report a problem
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 34: Magnetic Field- 1
Try yourself:If a charged particle at rest experiences no electromagnetic force,
Explanation
As the charged particle is at rest, its velocity, V = 0 and magnetic force, F = qVB = 0. Hence, we cannot determine whether a magnetic field is present or not.
But as the particle at rest experiences no electromagnetic force, the electric field must be zero. This is because electric force acts on a particle whether it is at rest or in motion.
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 34: Magnetic Field- 1
Try yourself:If a charged particle kept at rest experiences an electromagnetic force,
Explanation
As the charged particle is at rest, its velocity, V = 0 and magnetic force, F = qVB = 0. Hence, we cannot determine whether a magnetic field is present or not. But as the particle at rest experiences an electromagnetic force, the electric field must be non-zero. As electric force acts on a particle, whether it is at rest or in motion, an electric force must be present.
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 34: Magnetic Field- 1
Try yourself:If a charged particle projected in a gravity-free room deflects,
Explanation
As the particle gets deflected, a force acts on the particle. So, either it has got deflected due to the magnetic force or electric force; so, both the fields cannot be zero. Also, the particle can be deflected under the combined effect of magnetic and electric forces; so, both fields can be non-zero.
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 34: Magnetic Field- 1
Try yourself:A charged particle moves in a gravity-free space without change in velocity. Which of the following is/are possible?
Explanation
A charged particle can move in a gravity-free space without any change in velocity in the following three ways:
(1) E = 0, B = 0, i.e. no force is acting on the particle and hence, it moves with a constant velocity.
(2) E = 0, B ≠ 0. If magnetic field is along the direction of the velocity v, then the force acting on the charged particle will be zero, as F = q v × B = 0. Hence, the particle will not accelerate.
(3) If the force due to magnetic field and the force due to electric field counterbalance each other, then the net force acting on the particle will be zero and hence, the particle will move with a constant velocity.
Question for HC Verma Questions and Solutions: Chapter 34: Magnetic Field- 1
Try yourself:A charged particle moves along a circle under the action of possible constant electric and magnetic fields. Which of the following is possible?
Explanation
The electric field exerts a force q E on the charged particle, which always accelerates (increases the speed) the particle. The particle can never be rotated in a circle by the electric field because then the radius of the orbit will keep on increasing due to the acceleration, which is not possible. So, options (c) and (d) are incorrect. On the other hand, a magnetic field does not change the magnitude of the velocity but changes only the direction of the velocity. Since the particle is moving in a circle, where its speed remains constant and only the direction of velocity changes, so it can only be achieved if E = 0 and B ≠ 0.
Report a problem
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 34: Magnetic Field- 1
Try yourself:A charged particle goes undeflected in a region containing an electric and a magnetic field. It is possible that
Explanation
In option (a) velocity, electric field and magnetic field are parallel to each other. So, the particle may accelerate but always continue to travel in the same straight path or go undeflected.
Another possibility of the particle to go undeviated is that magnetic force acting on it is counterbalanced by electric force. This is possible if all the three, i.e. velocity, magnetic field and electric field are perpendicular to each other, so that magnetic force is balanced by electric force. So option (b) can also be one possibility. But (c) and (d) are wrong statements.
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 34: Magnetic Field- 1
Try yourself:If a charged particle moves unaccelerated in a region containing electric and magnetic fields
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 34: Magnetic Field- 1
Try yourself:Two ions have equal masses but one is singly-ionised and the other is doubly-ionised. They are projected from the same place in a uniform magnetic field with the same velocity perpendicular to the field.
Explanation
The radius of the orbit of a charged particle in an external magnetic field,
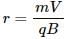
where r is the radius of the circle, m is the mass of the ion, V is the velocity with which the ion is projected, q is the charge on the ion and B is the uniform magnetic field.
Since the mass m, the velocity V and the magnetic field B are same for both the ions, r is inversely proportional to the charge on the ion.
Hence, the radius of the circle described by the singly-charged ion will be twice the radius of the circle described by doubly-ionised ion.
Moreover, as both the charges are projected from the same place, the two circles described by them will touch each other at the point of projection.
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 34: Magnetic Field- 1
Try yourself:An electron is moving along the positive x-axis. You want to apply a magnetic field for a short time so that the electron may reverse its direction and move parallel to the negative x-axis. This can be done by applying the magnetic field along
Explanation
Any magnetic field, except one parallel to the direction of velocity can change the direction of the particle. Therefore, either the magnetic field along y-axis or along z-axis can reverse the direction of the particle, as the velocity is along the x direction
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 34: Magnetic Field- 1
Try yourself: denote electric and magnetic fields in a frame S and
denote electric and magnetic fields in a frame S and  in another frame S' moving with respect to S at a velocity
in another frame S' moving with respect to S at a velocity  Two of the following equations are wrong. Identify them.
Two of the following equations are wrong. Identify them.
Explanation
Electric force due to a charged particle is q E and magnetic force is q V B.
We can sort out the two wrong equations using dimensional analysis. Now, equating the above two forces. we get:
E = V B
Hence, analysing the answers using dimensional analysis, we see that the second term on the RHS of the equations (b) and (c) are not dimensionally correct. Thus, the options (b) and (c) are wrong.
 denote electric and magnetic fields in a frame S and
denote electric and magnetic fields in a frame S and  in another frame S' moving with respect to S at a velocity
in another frame S' moving with respect to S at a velocity  Two of the following equations are wrong. Identify them.
Two of the following equations are wrong. Identify them.







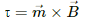
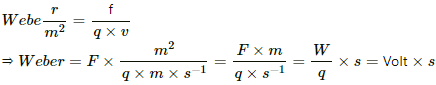

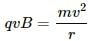
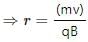
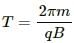
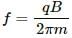

 cannot be parallel to velocity . Hence, the velocity vecv is perpendicular to the electric field
cannot be parallel to velocity . Hence, the velocity vecv is perpendicular to the electric field