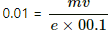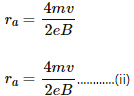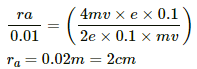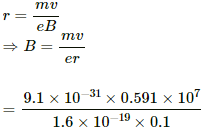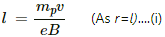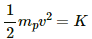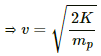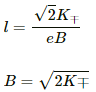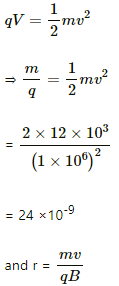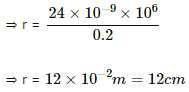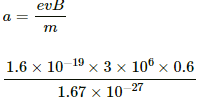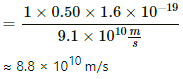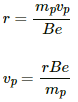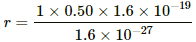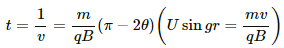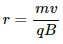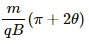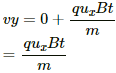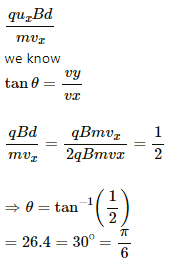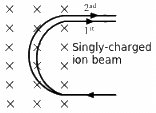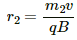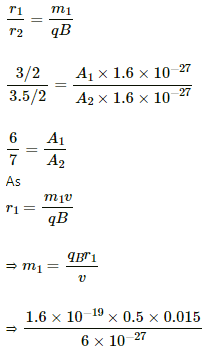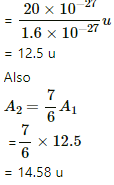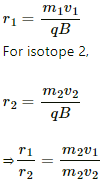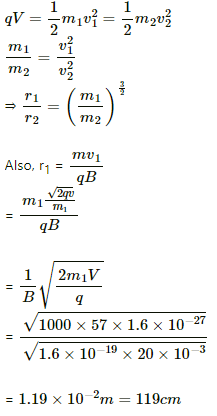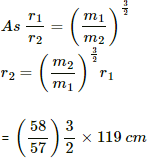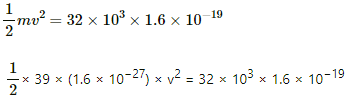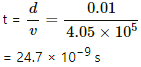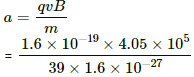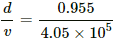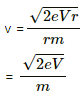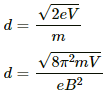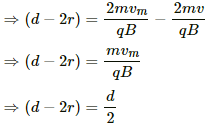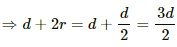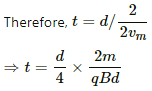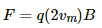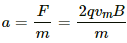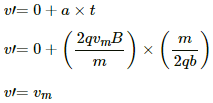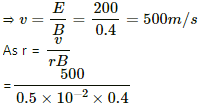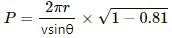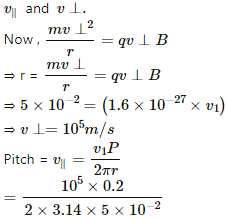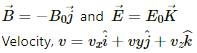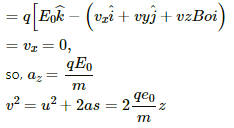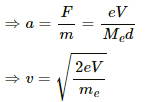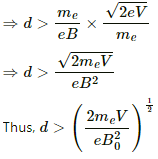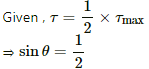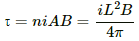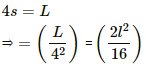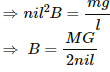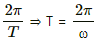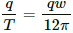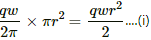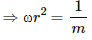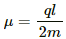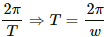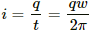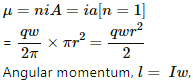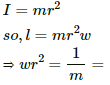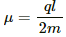HC Verma Questions and Solutions: Chapter 34: Magnetic Field- 3 | HC Verma Solutions - JEE PDF Download
Q.31. A proton describes a circle of radius 1 cm in a magnetic field of strength 0.10 T. What would be the radius of the circle described by an α-particle moving with the same speed in the same magnetic field?
Given:
Radius of the circle, r = 1 cm
Magnetic field = 0.10 T
We know that the charge of a proton is e and that of an alpha particle is 2e. Also, the mass of a proton is m and that of an aplha particle is 4m.
Suppose, both the particles are moving with speed v.
According to the question,where rp is the radius of the circle descrinbed by the proton.
On dividing equation (ii) by (i), we get:
Q.32. An electron of kinetic energy 100 eV circulates in a path of radius 10 cm in a magnetic field. Find the magnetic field and the number of revolutions per second made by the electron.
Given:
Kinetic energy of an electron = 100 eV
Radius of the circle = 10 cm
1/2mv2 = 100 eV = 1.6 × 10−17 J (1 eV = 1.6 × 10−19 J)
Here, m is the mass of an electron and v is the speed of an electron. Thus,
1/2 × 9.1 × 10−31 × v2 = 1.6 × 10−17 J
⇒ v2 = 0.35 × 1014
v = 0.591 × 107 m/s
Now,
B = 3.3613 × 10−4 T
Therefore, the applied magnetic field = 3.4 × 10−4 T
Number of revolutions per second of the electron,
= 0.094 × 108
= 9.4 × 106
f = 9.4 × 106
Q.33. Protons with kinetic energy K emerge from an accelerator as a narrow beam. The beam is bent by a perpendicular magnetic field, so that it just misses a plane target kept at a distance l in front of the accelerator. Find the magnetic field.
Given:
Kinetic energy of proton = K
Distance of the target from the accelerator = l
Therefore, radius of the circular orbit ≤ l
As per the question, the beam is bent by a perpendicular magnetic field.
We know
r = mv/eB
For a proton, the above equation can be written as:
Here,
mp is the mass of a proton v is the velocity e is the charge B is the magnetic field
putting the value of V in the equation (i),we get
Q.34. A charged particle is accelerated through a potential difference of 12 kV and acquires a speed of 1.0 × 106 m s−1. It is then injected perpendicularly into a magnetic field of strength 0.2 T. Find the radius of the circle described by it.
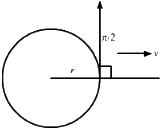
Given:
Applied potential difference, V = 12 kV = 12 × 103 V
Speed of a charged particle, v =1.0 × 106 m s−1
Magnetic field strength, B = 0.2 T
As per the question, a charged particle is injected perpendicularly into the magnetic field.
We know:
Q.35. Doubly-ionised helium ions are projected with a speed of 10 km s−1 in a direction perpendicular to a uniform magnetic field of magnitude 1.0 T. Find (a) the force acting on an ion (b) the radius of the circle in which it circulates and (c) the time taken by an ion to complete the circle.
Given:
Speed of the helium ions, v = 10 km s−1 = 104 m/s
Uniform magnetic field, B = 1.0 T
Charge on the helium ions = 2e
Mass of the helium ions, m = 4 × 1.6 × 10-27 kg
(a) The force acting on an ion,
F = qvBsinθ
= 2 × 1.6 × 10−19 × 104 × 1.0
= 3.2 × 10−15 N
(b) The radius of the circle in which it circulates,
(c) The time taken by an ion to complete the circle,
= 1.31 × 10−7 s
Q.36. A proton is projected with a velocity of 3 × 106 m s−1 perpendicular to a uniform magnetic field of 0.6 T. Find the acceleration of the proton.
Given:
Velocity of the proton, v = 3 × 106 m s−1
Uniform magnetic field, B = 0.6 T
As per the question, the proton is projected perpendicular to a uniform magnetic field.
We know,
F = mpa ....(i)
and
F = evBsinθ ....(ii)
On equating (i) and (ii), we get:
ma = evBsinθ (As θ = 90˚)
= 1.72 × 1014 m/s2
Q.37. (a) An electron moves along a circle of radius 1 m in a perpendicular magnetic field of strength 0.50 T. What would be its speed? Is it reasonable? (b) If a proton moves along a circle of the same radius in the same magnetic field, what would be its speed?
Given:
(a) Radius of the circle = 1 m
Magnetic field strength = 0.50 T
We know:where m_e is mass of the electron of the speed of the electron
Since, the speed of the electron moving along the circle is greater than the speed of light, it is not reasonable.
(b) For a proton,
where mp is the mass of the proton and vp is its speed.
r = 5 × 107 m/s
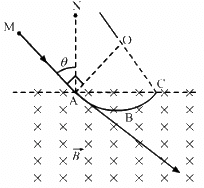
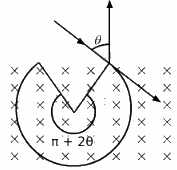
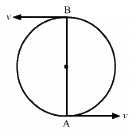
Q.38. A particle of mass m and positive charge q, moving with a uniform velocity v, enters a magnetic field B, as shown in the figure. (a) Find the radius of the circular arc it describes in the magnetic field. (b) Find the angle subtended by the arc at the centre. (c) How long does the particle stay inside the magnetic field? (d) Solve the three parts of the above problem if the charge q on the particle is negative.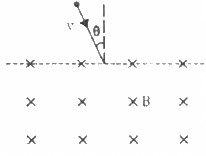
Given:-
Mass of the particle = m
Positive charge on the particle = q
Uniform velocity of the particle = v
Magnetic field = B
(a) The radius of the circular arc described by the particle in the magnetic field:-
We know
r = mv/qB
(b)
The angle subtended by the arc at the centre:-
Line MAB is tangent to arc ABC, so the angle described by the charged particle,
∠MAO = 90°
Now, ∠NAC = 90°
OAC = OCA = θ
[by geometry]
Then, AOC = 180° − (θ + θ) (By angle-sum property of a triangle)
= π − 2θ
(c) The time for which the particle stay inside the magnetic field:-
Distance covered by the particle inside the magnetic field,
l = rθ
(d) If the charge q on the particle is negative, then
(i) Radius of circular arc,
(ii) The centre of the arc will lie within the magnetic field. Therefore, the angle subtended by the arc = π + 2θ
(iii) Similarly, the time taken by the particle to cover the path inside the magnetic field =
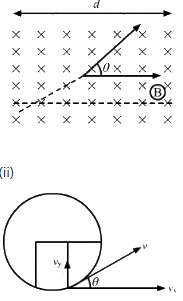
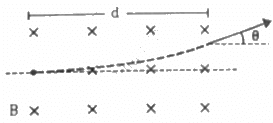
Q.39. A particle of mass m and charge q is projected into a region that has a perpendicular magnetic field B. Find the angle of deviation (figure) of the particle as it comes out of the magnetic field if the width d of the region is very slightly smaller than 
Given:
Mass of the particle = m
Charge of the particle = q
Magnetic field = B
As per the question, the particle is projected into a perpendicular magnetic field.
(a) When the width, d = mv/qB d is equal to the radius and θ is the angle between the radius and tangent, which is equal to π/2.
(b) When the width, d = mv/2qB
Width of the region in which a magnetic field is applied is half of the radius of the circular path described by the particle. As the magnetic force is acting only along the y direction, the velocity of the particle will remain constant along the x direction. So, if d is the distance travelled along the x axis, then d = vxt
t = d/Vx ...(i)
(i)
The acceleration along the x direction is zero. The force will act only along the y direction.
Using the equation of motion for motion along the y axis:
vy = uy + ayt
Putting the value of t from equation (i), we get:
(c) When the width, d = (c) When the width, d = 2mv/qB
Q.40. A narrow beam of singly-charged carbon ions, moving at a constant velocity of 6.0 × 104m s−1, is sent perpendicularly in a rectangular region of uniform magnetic field B = 0.5 T (figure). It is found that two beams emerge from the field in the backward direction, the separations from the incident beam being 3.0 cm and 3.5 cm. Identify the isotopes present in the ion beam. Take the mass of an ion = A(1.6 × 10−27) kg, where A is the mass number.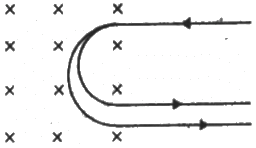
Given:
Velocity of a narrow beam of singly-charged carbon ions, v = 6.0 × 104 m s−1
Strength of magnetic field B = 0.5 T
Separations between the two beams from the incident beam are 3.0 cm and 3.5 cm.
Mass of an ion = A(1.6 × 10−27) kg
The radius of the curved path taken by the first beam, r_1 = m1v/qB
where m1 is the mass of the first isotope and q is the charge.
For the second beam:
where m2 is the mass of the first isotope and q is the charge.
= 20 × 10-27 kg
So, the two isotopes of carbon used are 12C6 and 14C6.
Q.41. Fe+ ions are accelerated through a potential difference of 500 V and are injected normally into a homogeneous magnetic field B of strength 20.0 mT. Find the radius of the circular paths followed by the isotopes with mass numbers 57 and 58. Take the mass of an ion = A (1.6 × 10−27) kg, where A is the mass number.
Given:
Potential difference through which the Fe+ ions are accelerated, V = 500 V
Strength of the homogeneous magnetic field, B = 20.0 mT = 20 × 10−3 T
Mass numbers of the two isotopes are 57 and 58.
Mass of an ion = A (1.6 × 10−27) kg
We know that the radius of the circular path described by a particle in a magnetic field,
r = mv/qB
For isotope 1,
As both the isotopes are accelerated via the same potential V, the K.E gained by the two particles will be same.
For the second isotope:
= 120 cm
Q.42. A narrow beam of singly charged potassium ions of kinetic energy 32 keV is injected into a region of width 1.00 cm with a magnetic field of strength 0.500 T, as shown in the figure. The ions are collected at a screen 95.5 cm away from the field region. If the beam contains isotopes of atomic weights 39 and 41, find the separation between the points where these isotopes strike the screen. Take the mass of a potassium ion = A (1.6 × 10−27) kg, where A is the mass number.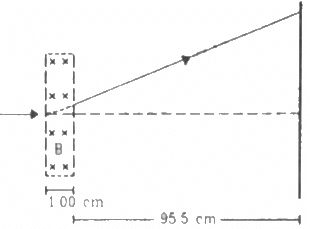
Kinetic energy of singly-charged potassium ions = 32 keV
Width of the magnetic region = 1.00 cm
Magnetic field's strength, B = 0.500 T
Distance between the screen and the region = 95.5 cm
Atomic weights of the two isotopes are 39 and 41.
Mass of a potassium ion = A (1.6 × 10−27) kg
For a singly-charged potassium ion K-39 :
Mass of K-39 = 39 × 1.6 × 10−27 kg,
Charge, q = 1.6 × 10−19 C
As per the question, the narrow beam of singly-charged potassium ions is injected into a region of magnetic field.
As
K.E = 32 keV
v = 4.05 × 105
We know that throughout the motion, the horizontal velocity remains constant.
So, the time taken to cross the magnetic field,
Now, the acceleration in the magnetic field region:
F = qvB = ma
= 5192 × 108 m/s2
Velocity in the vertical direction, vy = at
= 5193.53 × 108 × 24.7 × 10−9
= 12824.24 m/s
Time taken to reach the screen
Distance moved vertically in this time
= vy × t
= 12824.24 × 2358 × 10−9
= 3023.95×10-5 m
Vertical distance travelled by the particle inside magnetic field can be found out by using equaton of motion
v2 = 2aS
⇒ (12824.24)2 = 2 × 5192 × 108 × S
⇒ 15.83×10−5 = S
Net display from line
= 15.83×10−5+3023.95×10-5
= 3039.787×10−5 m.
For the potassium ion K-41l :
1/2× 41 × 1.6 × 10−27 v2= 32 × 103 × 1.6 × 10−9
⇒ v = 3.94×105 m/s
Similarly, acceleration,
a = 4805 × 108 m/s2
t = time taken for exiting the magnetic field
= 25.4 × 10−9 sec.
vy1= at (vertical velocity)
= 4805 × 108 × 25.4 × 10−9
= 12204.7× 10−9 m/s
Time to reach the screen
= 2423× 10−9 s.
Distance moved vertically
= 12204.7 × 2423 × 10−9
= 2957.1× 10−5
Now,
Vertical distance travelled by the particle inside magnetic field can be found out by using equaton of motion
v2 = 2aS
(12204.7)2 = 2 × 4805 × 108 S
⇒ S = 15.49× 10-5 m
Net distance travelled
= 15.49× 10-5 +2957.1× 10−5
= 2972.68× 10-5 m.
Net gap between K-39 and K-41
= 3039.787×10−5− 2972.68× 10-5
= 67 mm.
Q.43. The figure shows a convex lens of focal length 12 cm lying in a uniform magnetic field B of magnitude 1.2 T parallel to its principal axis. A particle with charge 2.0 × 10−3 C and mass 2.0 × 10−5 kg is projected perpendicular to the plane of the diagram with a speed of 4.8 m s−1. The particle moves along a circle with its centre on the principal axis at a distance of 18 cm from the lens. Show that the image of the particle moves along a circle and find the radius of that circle.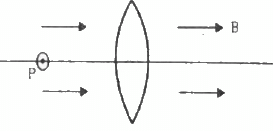
Given:-
Focal length of the convex lens = 12 cm
Uniform magnetic field, B = 1.2 T
Charge of the particle, q = 2.0 × 10−3 C
and mass, m = 2.0 × 10−5 kg
Speed of the particle, v = 4.8 m s−1
The distance of the particle from the lens = 18 cm
As per the question, the object is projected perpendicular to the plane of the paper.
Let the radius of the circle on which the object is moving be r.
We know:
Here, object distance, u = -18 cm
Using the lens equation
Image distance, v = 36 cm.
Let the radius of the circular path of image be r'.
So, magnification:
= 8 cm
Therefore, the radius of the circular path in which the image moves is 8 cm.
Q.44. Electrons emitted with negligible speed from an electron gun are accelerated through a potential difference V along the x-axis. These electrons emerge from a narrow hole into a uniform magnetic field B directed along this axis. However, some of the electrons emerging from the hole make slightly divergent angles, as shown in the figure. Show that these paraxial electrons are refocussed on the x-axis at a distance 
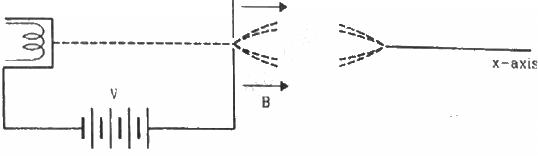
Given:-
Electrons are accelerated through a potential difference = V
Let the mass of an electron be m and the charge of an electron be e.
We know:-
Electric field, E = V/r
Force experienced by the electron, F = eE
Acceleration of the electron, a = eV/rm
Using the equation of motion
v2 − u2= 2 × a × s,
v2 = 2 × a × s (As u = 0)
Here, s = r
Time taken by electron to cover the curved path,
As the acceleration of the electron is along the y axis only, it travels along the x axis with uniform velocity.
Velocity of the electron moving along the field remains v.
Therefore, the distance at which the beam is refocused, d = v × T
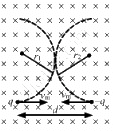
Q.45. Two particles, each with mass m are placed at a separation d in a uniform magnetic field B, as shown in the figure. They have opposite charges of equal magnitude q. At time t = 0, the particles are projected towards each other, each with a speed v. Suppose the Coulomb force between the charges is switched off. (a) Find the maximum value vm of the projection speed, so that the two particles do not collide. (b) What would be the minimum and maximum separation between the particles if v = vm/2? (c) At what instant will a collision occur between the particles if v = 2vm? (d) Suppose v = 2vm and the collision between the particles is completely inelastic. Describe the motion after the collision.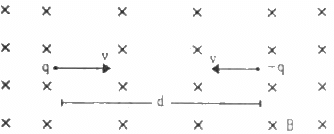
Given,
Mass of two particles = m
Distance between them = d
Both the particles have equal charges in magnitude but opposite polarity equal to q.
As per the question, both the particles are projected towards each other with equal speed v.
It is assumed that Coulomb force between the charges is switched off.
(a) The maximum value vm of the projection speed so that the two particles do not collide:-
Both the particles will not collide if d = r1 + r2 (where, r1 = r2 = radius of circular orbit described by the charged particles)
(b) The minimum and maximum separation between the particles if v = vm/2:-
Let the radius of the curved path taken by the particles, when they are projected with speed vm/2, be r.
So, minimum separation between the particles = (d - 2r)
Maximum distance separation = (d + 2r)
(c) The instant at which the collision occurs between the particles when
The particles will collide at a distance d/2 along the horizontal direction.
Let they collide after time t.
Velocity of the particles along the horizontal direction will remain the same.
(d) The motion of the two particles after collision when the collision is completely inelastic:-
v = 2vm
Let the particles collide at point P.
And at point P, both the particles will have motion in upward direction.
As the collision is inelastic they stick together.
Distance between centres = d
Velocity along the horizontal direction does not get affected due to the magnetic force.
At point P, velocities along the horizontal direction are equal and opposite. So, they cancel each other.
Velocity along the vertical direction (upward) will add up.
Magnetic force acting along the vertical direction,
Acceleration along the vertical direction,
Velocity of the combined mass at point P is along the vertical direction. So,
Hence, both the particles will behave as a combined mass and move with velocity vm.
Q.46. A uniform magnetic field of magnitude 0.20 T exists in space from east to west. With what speed should a particle of mass 0.010 g and with charge 1.0 × 10−5 C be projected from south to north so that it moves with uniform velocity?
Given:
Uniform magnetic field, B = 0.20 T
Mass of the particle, m = 0.010 g = 1 × 10−5 kg
Charge of the particle, q = 1.0 × 10−5 C
As per the question, if the particle has to move with uniform velocity in the region of the applied field, gravitational force experienced by the particle should be equal to the magnetic force experienced by the particle.
So, qvB = mg, where v is the uniform velocity and g is the acceleration due to gravity.
⇒ 1 × 10−5 × v × 2 × 10−1 = 1 × 10−5 × 9.8
⇒ v = 4.9 × 10 = 49 m/s
Q.47. A particle moves in a circle of diameter 1.0 cm under the action of a magnetic field of 0.40 T. An electric field of 200 V m−1 makes the path straight. Find the charge/mass ratio of the particle.
Given:
Diameter of the circle = 1.0 cm
Thus, radius of circle, r = = 0.5 × 10−2 m,
Magnetic field, B = 0.40 T
Electric field, E = 200 V m−1.
As per the question, the particle is moving in a circle under the action of a magnetic field. But when an electric field is applied on the particle, it moves in a straight line.
So, we can write:
Fe = Fm
qE = qvB, where q is the charge and v is the velocity of the particle.
= 2.5 × 105 c /kg
Q.48. A proton goes undeflected in a crossed electric and magnetic field (the fields are perpendicular to each other) at a speed of 2.0 × 105 m s−1. The velocity is perpendicular to both the fields. When the electric field is switched off, the proton moves along a circle of radius 4.0 cm. Find the magnitudes of the electric and magnetic fields. Take the mass of the proton = 1.6 × 10−27 kg.
Given:
Mass of the proton, m = 1.6 × 10−27 kg
Speed of the proton inside the crossed electric and magnetic field, v = 2.0 × 105 ms−1
As per the question, the proton is not deflected under the combined action of the electric and magnetic fields. Thus, the forces applied by both the fields are equal and opposite.
That is, qE = qvB
⇒ E = vB ...(1)
But when the electric field is switched off, the proton moves in a circle due to the force of the magnetic field.
Radius of the circle, r = 4.0 cm = 4 × 10−2 m
Putting the value of B in equation (1), we get:
E = 2 × 105 × 0.05
= 1 × 104 N/c
Q.49. A particle with a charge of 5.0 µC and a mass of 5.0 × 10−12 kg is projected with a speed of 1.0 km s−1 in a magnetic field of magnitude 5.0 mT. The angle between the magnetic field and the velocity is sin−1 (0.90). Show that the path of the particle will be a helix. Find the diameter of the helix and its pitch.
Given:
Charge of the particle, q = 5 µC = 5 × 10−6 C
Magnetic field intensity, B = 5 × 10−3 T
Mass of the particle, m = 5 × 10−12 kg
Velocity of projection, v = 1 Km/s = 103 m/s
Angle between the magnetic field and velocity, θ= sin−1(0.9)
Component of velocity perpendicular to the magnetic field,
Component of velocity in the direction of magnetic field,
Since there are no forces in the horizontal direction (the direction of magnetic field), the particle moves with uniform velocity.
The velocity has a vertical component along which it accelerates with an acceleration a and moves in a circular cross-section. Thus, it moves in a helix.
Hence, diameter of the helix, 2r = 0.36 m = 36 cm
Pitch,
= 0.55 m = 55cm
Q.50. A proton projected in a magnetic field of 0.020 T travels along a helical path of radius 5.0 cm and pitch 20 cm. Find the components of the velocity of the proton along and perpendicular to the magnetic field. Take the mass of the proton = 1.6 × 10−27 kg
Mass of the proton, mp = 1.6 × 10−27 kg
Magnetic field intensity, B = 0.02 T
Radius of the helical path, r = 5 cm = 5 × 10−2 m
Pitch of the helical path, p = 20cm = 2 × 10−1 m
We know that for a helical path, the velocity of the proton has two components,
= 0.6369 × 105
= 6.4 × 104 m/s
Q.51. A particle of mass m and charge q is released from the origin in a region in which the electric field and magnetic field are given by 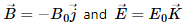 Find the speed of the particle as a function of its z-coordinate.
Find the speed of the particle as a function of its z-coordinate.
Given:
Mass of the particle = m
Charge of the particle = q
Electric field and magnetic field are given by
So, total force on the particle,
F = q (E + v × B)
Here, z is the distance along the z-direction.
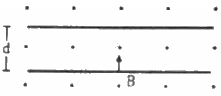
Q.52. An electron is emitted with negligible speed from the negative plate of a parallel-plate capacitor charged to a potential difference V. The separation between the plates is d and a magnetic field B exists in the space, as shown in the figure. Show that the electron will fail to strike the upper plates if 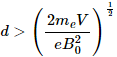
Given:-
Potential difference across the plates of the capacitor = V
Separation between the plates = d
Magnetic field intensity = B
The electric field set up between the plates of a capacitor, E = V/d
The electron will move in a circular path due to the given magnetic field. Radius of the circular path,
And the electron will fail to strike the upper plate only when the radius of the circular path will be less than d, i.e d > r
Q.53. A rectangular coil of 100 turns has length 5 cm and width 4 cm. It is placed with its plane parallel to a uniform magnetic field and a current of 2 A is sent through the coil. Find the magnitude of the magnetic field B if the torque acting on the coil is 0.2 N m−1.
Given:
No. of turns in the coil, n = 100
Area of the coil, A = 5 × 4 cm2 = 20 × 10−4 m2
Magnitude of current = 2 A
Torque acting on the coil, τ = 0.2 N m−1
τ = niA × B
⇒τ = niBA sin 90°
⇒ 0.2 = 100 × 2 ×20 × 10−4 × B
⇒ B = 0.5 T
Q.54. A 50-turn circular coil of radius 2.0 cm carrying a current of 5.0 A is rotated in a magnetic field of strength 0.20 T. (a) What is the maximum torque that acts on the coil? (b) In a particular position of the coil, the torque acting on it is half of this maximum. What is the angle between the magnetic field and the plane of the coil?
Given:
No. of turns of the coil, n = 50
Magnetic field intensity, B = 0.20 T = 2 × 10−1 T
Radius of the coil, r = 0.02 m = 2 × 10−2 m
Magnitude of current =5 A
Torque acting on the coil,
τ = niABsinθ
Here, A is the area of the coil and θ is the angle between the area vector and the magnetic field.
τ is maximum when θ = 90°.
τmax = niABsin90°
= 50 × 5 × 3.14 × 4 × 10−4 × 2 × 10−1
= 6.28 × 10−2 N-m
⇒ θ = 30°
So, the angle between the magnetic field and the plane of the coil = 90° − 30° = 60°.
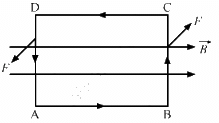
Q.55. A rectangular loop of sides 20 cm and 10 cm carries a current of 5.0 A. A uniform magnetic field of magnitude 0.20 T exists parallel to the longer side of the loop. (a) What is the force acting on the loop? (b) What is the torque acting on the loop?
Let ABCD be the rectangular loop.
Given:
No. of turns of the coil, n = 50
Magnetic field intensity, B = 0.20 T = 2 × 10−1 T
Magnitude of current, I = 5 A
Length of the loop, l = 20 cm = 20 × 10−2 m,
Breadth of the loop, w = 10 cm = 10 × 10−2 m,
So, area of the loop, A = lw = 0.02 m2,
fig
(a) There is no force on the sides ab and cd, as they are along the magnetic field.
But the force on the sides ad and bc are equal and opposite; so, they cancel each other.
Hence, the net force on the loop is zero.
(b) Torque acting on the coil,
τ = niABsinθ
Here, A is the area of the coil and θ is the angle between the area vector and magnetic field.
τ = niABsin90°
= 1 × 5 × 0.02 × 0.2
= 0.02 N-m
So, the torque acting on the loop is 0.02 N-m and is parallel to the shorter side.
Q.56. A circular coil of radius 2.0 cm has 500 turns and carries a current of 1.0 A. Its axis makes an angle of 30° with the uniform magnetic field of magnitude 0.40 T that exists in the space. Find the torque acting on the coil.
Given:
No. of turns of the coil, n = 500
Magnetic field intensity, B = 0.40 T = 4 × 10−1 T
Radius of the coil, r = 2 cm = 2 × 10−2 m
Magnitude of current, i = 1 A
Angle between the area vector and magnetic field, θ = 30°
Torque acting on the coil,
τ = niABsinθ
Here, A is the area of the coil.
τ = 500 × 1 × 3.14 × 4 × 10−4 ×4×10−1 × 1/2
= 12.56 × 10−2
= 0.1256 = 0.13 N-m
Q.57. A circular loop carrying a current i is made of a wire of length L. A uniform magnetic field B exists parallel to the plane of the loop. (a) Find the torque on the loop. (b) If the same length of the wire is used to form a square loop, what would be the torque? Which is larger?
Given,
Magnetic field intensity = B
Circumference, L = 2πr, where r is the radius of the coil.
So, area of the coil, A = l2/4π
Magnitude of current = i
Torque acting on the coil,
τ = niABsinθ, where θ is the angle between the area vector and the magnetic field.
(b) Let s be the length of the square loop.
So, the torque on the circular loop is larger.
Q.58. A square coil of edge l and with n turns carries a current i. It is kept on a smooth horizontal plate. A uniform magnetic field B exists parallel to an edge. The total mass of the coil is M. What should be the minimum value of B for which the coil will start tipping over?
Given:
Number of turns in the coil = n
Edge of the square loop = l
Magnetic field intensity = B
Magnitude of current = i
Angle between area vector and magnetic field, θ = 90°
Torque acting on the coil due to magnetic field,
τ = niABsinθ
Here, A is the area of the coil.
Torque produced due to weight, τweight = mgl/2
For the coil to start tipping over,
τ ≥ τweight
For minimum value of B,
τ = τ weight
Q.59. Consider a non-conducting ring of radius r and mass m that has a total charge q distributed uniformly on it. The ring is rotated about its axis with an angular speed ω. (a) Find the equivalent electric current in the ring. (b) Find the magnetic moment µ of the ring. (c) Show that 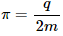 l, where l is the angular momentum of the ring about its axis of rotation.
l, where l is the angular momentum of the ring about its axis of rotation.
Given:
Radius of the ring = r
Mass of the ring = m
Total charge of the ring = q
(a) Angular speed, ω =
Current in the ring i ,=
(b) For a ring of area A with current i, magnetic moment,
(c) Angular momentum, l = Iω
where I is moment of inertia of the ring about its axis of rotation.
I =mr2
so , I =mr2ω
Putting this value in equation (i), we get:
Q.60. Consider a non-conducting plate of radius r and mass m that has a charge q distributed uniformly over it. The plate is rotated about its axis with an angular speed ω. Show that the magnetic moment µ and the angular momentum l of the plate are related as 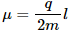
Given:
Radius of the ring = r
Mass of the ring = m
Total charge of the ring = q
Angular speed, w =
Current in the ring,
For the ring of area A with current i, magnetic moment,
where I is the moment of inertia of the ring about its axis of rotation.
Putting this value in equation (i), we get:
Q.61. Consider a solid sphere of radius r and mass m that has a charge q distributed uniformly over its volume. The sphere is rotated about its diameter with an angular speed ω. Show that the magnetic moment µ and the angular momentum l of the sphere are related as 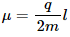
Considering the strip of width dx at a distance x from the centre of the sphere.
Small area of the strip is given as,
da = 4π x dx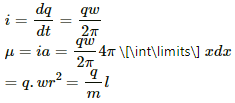
|
134 docs
|
FAQs on HC Verma Questions and Solutions: Chapter 34: Magnetic Field- 3 - HC Verma Solutions - JEE
| 1. What is the magnetic field? |  |
| 2. How is the direction of the magnetic field determined? |  |
| 3. How can the strength of a magnetic field be calculated? |  |
| 4. What is the difference between a magnetic field and an electric field? |  |
| 5. Can the magnetic field be shielded or blocked? |  |