Complete Guide to Fractions | The Complete SAT Course - Class 10 PDF Download
| Table of contents |

|
| What are Fractions? |

|
| Reducing Fractions |

|
| Adding or Subtracting Fractions |

|
| Multiplying Fractions |

|
| Dividing Fractions |

|
| Decimal Points |

|
What are Fractions?
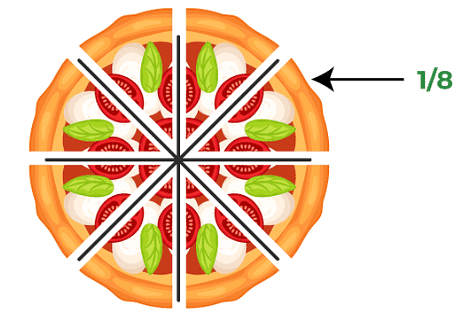
Fractions are pieces of a whole. They are expressed as the amount you have (the numerator) over the whole (the denominator).
Special Fractions
1. A number over itself equals 1
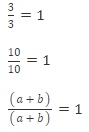
2. A whole number can be expressed as itself over 1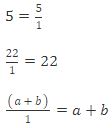
3. 0 divided by any number is 0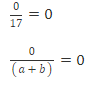
There is one exception to this rule:
0/0 = undefined. The reason for this lies in the next rule.
Any number divided by 0 is undefined: Zero cannot act as a denominator. For more information on this check out our guide to advanced integers. But for now all that matters is that you know that 0 cannot act as a denominator.
Reducing Fractions
Reducing fractions means simplifying the fraction to its lowest terms. It involves dividing both the numerator and denominator of a fraction by their greatest common factor (GCF) to obtain an equivalent fraction with smaller numbers.
For example, consider the fraction 12/18. The GCF of 12 and 18 is 6, so we divide both the numerator and denominator by 6 to get:
12/18 = (12 ÷ 6) / (18 ÷ 6) = 2/3
If your fraction is 3/12, then it can be written as 1/4. Why? Because both 3 and 12 are divisible by 3.
3/3 = 1 and 12/3 = 4.
So your final fraction is 1/4

Adding or Subtracting Fractions
Adding or subtracting fractions is possible only when the fractions have the same denominator. If they don't have the same denominator, we must find a common denominator for them first.
To find a common denominator, we must find the lowest common multiple (LCM) of the denominators. For example, let's say we want to add the following two fractions:
1/4 + 2/3
The LCM of 4 and 3 is 12. To convert the first fraction to have a denominator of 12, we need to multiply both the numerator and denominator by 3:
1/4 x 3/3 = 3/12
To convert the second fraction to have a denominator of 12, we need to multiply both the numerator and denominator by 4:
2/3 x 4/4 = 8/12
Now that both fractions have the same denominator, we can add them:
3/12 + 8/12 = 11/12
We can simplify the answer to a mixed number or a fraction in lowest terms, depending on the requirements of the question.
When subtracting fractions, we follow the same process of finding a common denominator, but instead of adding the numerators, we subtract them.
For example: 2/5 - 1/10
The LCM of 5 and 10 is 10. To convert the first fraction to have a denominator of 10, we need to multiply both the numerator and denominator by 2:
2/5 x 2/2 = 4/10
To convert the second fraction to have a denominator of 10, we need to multiply both the numerator and denominator by 1:
1/10 x 10/10 = 1/10
Now that both fractions have the same denominator, we can subtract them:
4/10 - 1/10 = 3/10
We can simplify the answer to a fraction in lowest terms if required.
Multiplying Fractions
Multiplying fractions is a bit simpler than adding or dividing fractions. There is no need to find a common denominator—you can just multiply the fractions straight across.
To multiply a fraction, first multiply the numerators. This product becomes your new numerator.
Then, multiply the denominators together to get your new denominator. Here is an example:
2/3 × 4/5 = ?
2 × 4 = 8
3 × 5 = 15
So, 2/3 × 4/5 = 8/15.
Notice that in this case, we simply multiplied 2 and 4 to get 8, and 3 and 5 to get 15. This is because there are no common factors between 2 and 3, or between 4 and 5. However, if there are common factors between the numerators and denominators, it is important to cancel them out before multiplying. This process is called simplifying the fractions before multiplying.
Dividing Fractions
In order to divide fractions, we must first take the reciprocal (the reversal) of one of the fractions. Afterwards, we simply multiply the two fractions together. Why do we do this? Because division is the opposite of multiplication, so we must reverse one of the fractions to turn it back into a multiplication question.
To divide fractions:
- Flip the second fraction (the divisor) upside down (take its reciprocal).
- Multiply the first fraction (the dividend) by the reciprocal of the second fraction (the divisor).
Here's an example: 3/4 ÷ 2/5
We want to divide 3/4 by 2/5.
First, we flip the second fraction, so that the question becomes:
3/4 × 5/2
Next, we multiply the numerators and denominators straight across:
(3 × 5) / (4 × 2) = 15/8
So, 3/4 ÷ 2/5 = 15/8.
Decimal Points
Decimal points are a way to represent fractions or parts of a whole in the decimal system. The decimal point separates the whole number from the fractional part of a number, and is denoted by a period or dot (.).
For example, the fraction 3/4 can be expressed as a decimal by dividing 3 by 4:
3 ÷ 4 = 0.75
So, 3/4 is equivalent to 0.75 when expressed as a decimal.
- Decimal points can also be used to represent numbers that are not fractions, such as 0.5 which represents half of a whole, or 1.25 which represents one whole plus a quarter of a whole.
- Decimal points can be added, subtracted, multiplied, and divided just like whole numbers. For example, to add 1.25 and 0.75, we can line up the decimal points and add the digits:
1.25 + 0.75 = 2.00
So, 1.25 + 0.75 = 2.00, or simply 2 when the trailing zeros are removed.
|
433 videos|220 docs|166 tests
|















