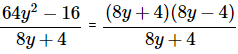SAT Exam > SAT Notes > Mathematics for Digital SAT > Factoring Solved Examples
Factoring Solved Examples | Mathematics for Digital SAT PDF Download
Example 1: Algebra
If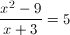 
, and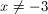 
, what is the value of 
?
(a) 0
(b) -6
(c) 6
(d) 8
(e) –8
Correct Answer is Option (d)
The numerator on the left can be factored so the expression becomeswhich can be simplified to (x - 3) = 5.
Then you can solve for x by adding 3 to both sides of the equation, so x = 8
Example 2: Factoring
Factor the following variable (x2 + 18x + 72)
(a) (x + 6) (x – 12)
(b) (x – 6) (x – 12)
(c) (x + 18) (x + 72)
(d) (x + 6) (x + 12)
(e) (x – 6) (x + 12)
Correct Answer is Option (d)
You need to find two numbers that multiply to give 72 and add up to give 18
easiest way: write the multiples of 72:
1, 72
2, 36
3, 24
4, 18
6, 12: these add up to 18
(x + 6)(x + 12)
Example 3: How To Factor A Variable
Factor 9x2 + 12x + 4.
(a) (9x + 4)(9x + 4)
(b) (9x + 4)(9x – 4)
(c) (3x – 2)(3x – 2)
(d) (3x + 2)(3x – 2)
(e) (3x + 2)(3x + 2)
Correct Answer is Option (e)
Nothing common cancels at the beginning. To factor this, we need to find two numbers that multiply to 9 x 4 = 36 and sum to 12. 6 and 6 work.
So 9x2 + 12x + 4 = 9x2 + 6x + 6x + 4
Let's look at the first two terms and last two terms separately to begin with. 9x2 + 6x can be simplified to 3x(3x + 2) and 6x + 4 can be simplified into 2(3x + 2). Putting these together gets us
9x2 + 12x + 4
= 9x2 + 6x + 6x + 4
= 3x(3x + 2) + 2(3x + 2)
= (3x + 2)(3x + 2)
This is as far as we can factor.
Example 4 : Factoring
Factor: −12x2 + 27
(a) −3(2x + 3)(2x + 3)
(b) −3(2x + 3)(2x − 3)
(c) −3(4x2 − 9)
(d) (2x + 3)(2x + 3)
(e) (2x + 3)(2x − 3)
Correct Answer is Option (b)
We can first factor out −3:
−3(4x2 - 9)
This factors further because there is a difference of squares:
−3(2x + 3)(2x − 3)
 |
Download the notes
Factoring Solved Examples
|
Download as PDF |
Download as PDF
Example 5: How To Factor A Variable
Factor to the simplest form: x3 + 2x2 + a + bx2 + 2
(a) 3x3 + a + b + 2
(b) x3 + (2 + b)(x2) + a + 2
(c) x2(x + 2 + b + a + 2)
(d) x2(x + 2 + b) + a + 2
(e) x(x2 + 2x + bx) + a + 2
Correct Answer is Option (d)
Group all the terms with the x variable.
x3 + 2x2 + a + bx2 + 2 = (x3 + 2x2 + bx2) + a + 2
Pull out an x2 term from parentheses.
(x3 + 2x2 + bx2) + a + 2 = x2(x + 2 + b) + a + 2
There are no more common factors.
The correct answer is: x2(x + 2 + b) + a + 2
 |
Take a Practice Test
Test yourself on topics from SAT exam
|
Practice Now |
Practice Now
Example 6: Algebra
Factor and simplify: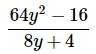 
(a) 8y − 12
(b) −4
(c) 8y
(d) 8y − 4
(e) 8y + 4
Correct Answer is Option (d)
64y2 − 16 is a difference of squares.
The difference of squares formula is a2 − b2 = (a − b)(a + b).
Therefore,
= 8y − 4
The document Factoring Solved Examples | Mathematics for Digital SAT is a part of the SAT Course Mathematics for Digital SAT.
All you need of SAT at this link: SAT
|
185 videos|124 docs|75 tests
|
About this Document
4.81/5
Rating
Apr 18, 2025
Last updated
Document Description: Factoring Solved Examples for SAT 2025 is part of Mathematics for Digital SAT preparation.
The notes and questions for Factoring Solved Examples have been prepared according to the SAT exam syllabus. Information about Factoring Solved Examples covers topics
like and Factoring Solved Examples Example, for SAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Factoring Solved Examples.
Introduction of Factoring Solved Examples in English is available as part of our Mathematics for Digital SAT
for SAT & Factoring Solved Examples in Hindi for Mathematics for Digital SAT course.
Download more important topics related with notes, lectures and mock test series for SAT
Exam by signing up for free. SAT: Factoring Solved Examples | Mathematics for Digital SAT
Description
Full syllabus notes, lecture & questions for Factoring Solved Examples | Mathematics for Digital SAT - SAT | Plus excerises question with solution to help you revise complete syllabus for Mathematics for Digital SAT | Best notes, free PDF download
Information about Factoring Solved Examples
In this doc you can find the meaning of Factoring Solved Examples defined & explained in the simplest way possible. Besides explaining types of
Factoring Solved Examples theory, EduRev gives you an ample number of questions to practice Factoring Solved Examples tests, examples and also practice SAT
tests
Related Searches
Factoring Solved Examples | Mathematics for Digital SAT
,Extra Questions
,Objective type Questions
,Factoring Solved Examples | Mathematics for Digital SAT
,past year papers
,Viva Questions
,MCQs
,Free
,Sample Paper
,study material
,Important questions
,practice quizzes
,Summary
,Previous Year Questions with Solutions
,Factoring Solved Examples | Mathematics for Digital SAT
,Exam
,mock tests for examination
,video lectures
,shortcuts and tricks
,Semester Notes
,ppt
;
Additional Information about Factoring Solved Examples for SAT Preparation
Factoring Solved Examples Free PDF Download
The Factoring Solved Examples is an invaluable resource that delves deep into the core of the SAT exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Factoring Solved Examples now and kickstart your journey towards success in the SAT exam.
Importance of Factoring Solved Examples
The importance of Factoring Solved Examples cannot be overstated, especially for SAT aspirants.
This document holds the key to success in the SAT exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Factoring Solved Examples Notes
Factoring Solved Examples Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Factoring Solved Examples.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Factoring Solved Examples Notes on EduRev are your ultimate resource for success.
Factoring Solved Examples SAT Questions
The "Factoring Solved Examples SAT Questions" guide is a valuable resource for all aspiring students preparing for the
SAT exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Factoring Solved Examples on the App
Students of SAT can study Factoring Solved Examples alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Factoring Solved Examples,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Factoring Solved Examples is prepared as per the latest SAT syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup