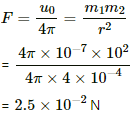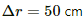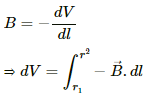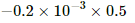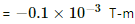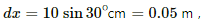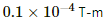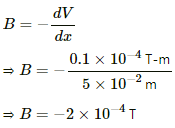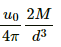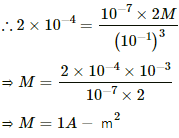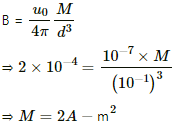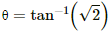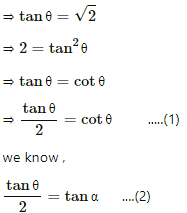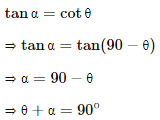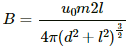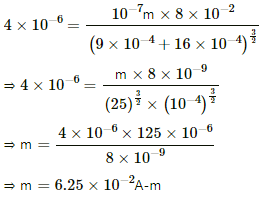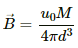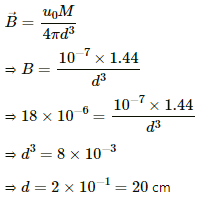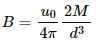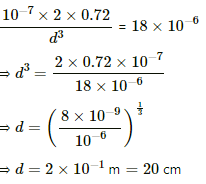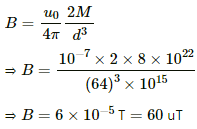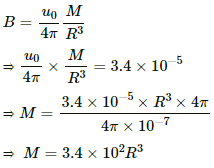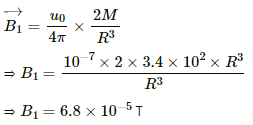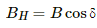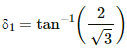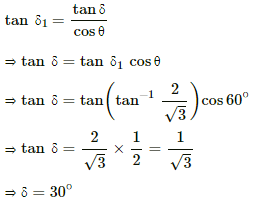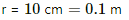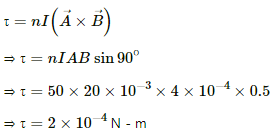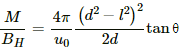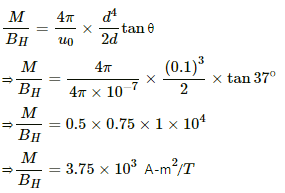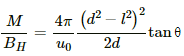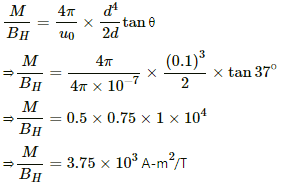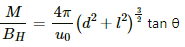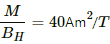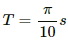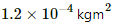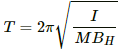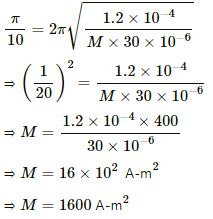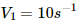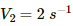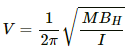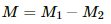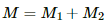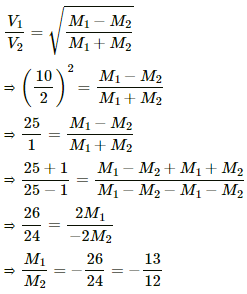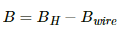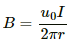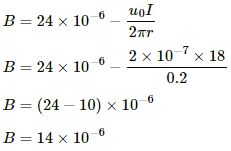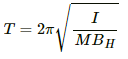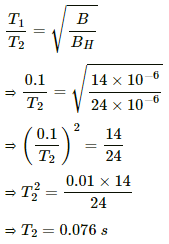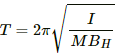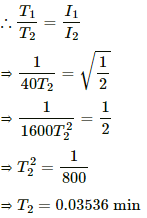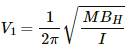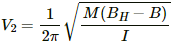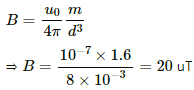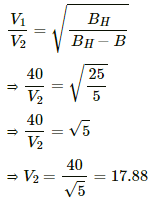HC Verma Questions and Solutions: Chapter 36: Permanent Magnets- 2 | HC Verma Solutions - JEE PDF Download
Exercises
Q.1. A long bar magnet has a pole strength of 10 Am. Find the magnetic field at a point on the axis of the magnet at a distance of 5 cm from the north pole of the magnet.
Pole strength of the bar magnet, m = 10 Am
Distance of the point from the north pole of the bar magnet, r = 5 cm = 0.05 m
We know,
The magnetic field due to magnetic charge (B) is given by
Q.2. Two long bare magnets are placed with their axes coinciding in such a way that the north pole of the first magnet is 2.0 cm from the south pole of the second. If both the magnets have a pole strength of 10 Am, find the force exerted by one magnet of the other.
Given:
Pole strength = m1 = m2 = 10 Am
Distance between the north pole of the first magnet and the south pole of the second magnet, r = 2 cm = 0.02 m
We know,
Force (F) exerted by two magnetic poles on each other is given by
Q.3. A uniform magnetic field of 0.20 x 10-3T exists in the space. Find the change in the magnetic scalar potential as one moves through 50 cm along the field.
Given :
Magnetic field in the space, B = 0.20 x 10-3T
Distance moved,
We know,
Since the magnetic field is uniform, it can come out of the integration sign.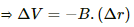
here, ΔV is the change in the potential
∴ Change in the potential =
Here, the negative sign shows that the potential decreases.
Q.4. Figure shows some of the equipotential surfaces of the magnetic scalar potential. Find the magnetic field B at a point in the region.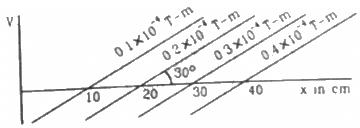
Given :
Perpendicular distance,
Change in the potential, dV =
We know that the relation between the potential and the field is given by
B is perpendicular to the equipotential surface. Here, it is at angle of 120° with the positive x-axis.
Q.5. The magnetic field at a point, 10 cm away from a magnetic dipole, is found to be 2.0 x 10-4 T. Find the magnetic moment of the dipole if the point is (a) in end-on position of the dipole and (b) in broadside-on position of the dipole.
Given:
Magnetic field strength, B = 2 x 10-4 T
Distance of the point from the dipole, d = 10 cm = 0.1 m
(a) If the point is at the end-on position:
The magnetic field (B) on the axial point of the dipole is given by B =
Here , M is the magnetic moment of the dipole that we need to find out .
(b) If the point is at broadside-on position (equatorial position):
The magnetic field (B) is given by
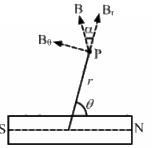
Q.6. Show that the magnetic field at a point due to a magnetic dipole is perpendicular to the magnetic axis if the line joining the point with the centre of the dipole makes an angle of 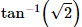 with the magnetic axis.
with the magnetic axis.
Given :
Angle made by observation point P with the axis of the dipole,
On comparing (1) and (2), we get
Hence, the magnetic field due to the dipole is perpendicular to the magnetic axis.
Q.7. A bar magnet has a length of 8 cm. The magnetic field at a point at a distance 3 cm from the centre in the broadside-on position is found to be 4 x 10-6T. Find the pole strength of the magnet.
Given:
Length of the magnet, 2l = 8 cm = 8 x 10-2 m
Distance of the observation point from the centre of the dipole, d = 3 cm
Magnetic field in the broadside-on position, B = 4 x 10-6T
The magnetic field due to the dipole on the equatorial point (B) is given by
Here, m is the pole strength of the magnet.
On substituting the respective values, we get
Q.8. A magnetic dipole of magnetic moment 1.44 Am2 is placed horizontally with the north pole pointing towards north. Find the position of the neutral point if the horizontal component of the earth's magnetic field is 18 μT.
Given :
Magnetic moment of the magnetic dipole, M = 1.44 A-m2
Horizontal component of Earth's magnetic field, BH = 18 μT
We know that for a magnetic dipole with pole pointing to the north, the neutral point always lies in the broadside-on position.
Let d be the perpendicular distance of the neutral point from mid point of the magnet.
The magnetic field due to the dipole at the broadside-on position (B) is given by
This magnetic field strength should be equal to the horizontal component of Earth's magnetic field at that point, that is, BH due to Earth.
Thus,
Q.9. A magnetic dipole of magnetic moment 0.72 A m2 is placed horizontally with the north pole pointing towards south. Find the position of the neutral point if the horizontal component of the earth's magnetic field is 18 μT.
Given :
Magnetic moment of the magnetic dipole, M = 0.72 Am2
Horizontal component of Earth's magnetic field, BH = 18 μT
Let d be the distance of the neutral point from the south of the dipole.
When the magnet is such that its north pole faces the geographic south of Earth, the neutral point lies along the axial line of the magnet.
Thus, the magnetic field on the axial point of the dipole (B) is given by
This magnetic field strength should be equal to the horizontal component of Earth's magnetic field.
Thus,
Q.10. A magnetic dipole of magnetic moment 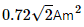 is placed horizontally with the north pole pointing towards east. Find the position of the neutral point if the horizontal component of the earth's magnetic field is 18 μT.
is placed horizontally with the north pole pointing towards east. Find the position of the neutral point if the horizontal component of the earth's magnetic field is 18 μT.
Given :
Magnetic moment of magnetic dipole,
Horizontal component of the earth's magnetic field,
Let d be the distance of neutral point from the dipole.
Magnetic field due to the bar magnet (B) on the equatorial line of the dipole is given by,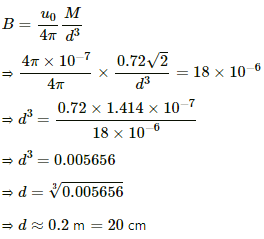
Q.11. The magnetic moment of the assumed dipole at the earth's centre is 8.0 × 1022 A m2. Calculate the magnetic field B at the geomagnetic poles of the earth. Radius of the earth is 6400 km.
Given :
Magnetic moment of dipole at Earth's centre, M = 8.0 x 1022 Am2
Radius of Earth, d = 6400 km
The geomagnetic pole is at the end of the position (axial) of Earth.
Thus, the magnetic field at the axial point of the dipole (B) is given by
Q.12. If the earth's magnetic field has a magnitude 3.4 × 10−5 T at the magnetic equator of the earth, what would be its value at the earth's geomagnetic poles?
Given :
Magnetic field at the magnetic equator, B = 3.4 × 10−5 T
Let M be the magnetic moment of Earth's magnetic dipole and R be the distance of the observation point from the centre of Earth's magnetic dipole.
As the point on the magnetic equator is on the equatorial position of Earth's magnet, the magnetic field at the equatorial point (B) is given by
As the magnetic field on Earth's geomagnetic poles lies on the axial point of the magnetic dipole, the magnetic field at the axial point (B1) is given by
Q.13. The magnetic field due to the earth has a horizontal component of 26 μT at a place where the dip is 60°. Find the vertical component and the magnitude of the field.
Given :
Horizontal component of Earth's magnetic field, B = 26 μT
Angle of dip, δ = 60°
The horizontal component of Earth's magnetic field (BH) is given by
Here,
B = Total magnetic field of Earth
On substituting the respective values, we get
The vertical component of Earth's magnetic field (By) is given by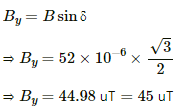
Q.14. A magnetic needle is free to rotate in a vertical plane which makes an angle of 60° with the magnetic meridian. If the needle stays in a direction making an angle of 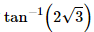 with the horizontal, what would be the dip at that place?
with the horizontal, what would be the dip at that place?
Given :
Angle made by the magnetic meridian with the plane of rotation of the needle , θ = 60°
Angle made by the needle with the horizontal,
If δ is the angle of dip , then
Q.15. The needle of a dip circle shows an apparent dip of 45° in a particular position and 53° when the circle is rotated through 90°. Find the true dip.
Given :
Apparent dip shown by the needle of the dip circle , δ1 = 45°
Dip shown by the needle of the dip circle on rotating the circle, δ2 =53°
true dip (δ) is given by
Q.16. A tangent galvanometer shows a deflection of 45° when 10 mA of current is passed through it. If the horizontal component of the earth's magnetic field is BH = 3.6 x 10-5 T and radius of the coil is 10 cm, find the number of turns in the coil.
Given :
Horizontal component of Earth's magnetic field, BH = 3.6 x 10-5 T
Deflection shown by the tangent galvanometer, θ = 45º
Current through the galvanometer, l = 10 mA = 10-2 A
Radius of the coil,
Number of turns in the coil, n = ?
We know,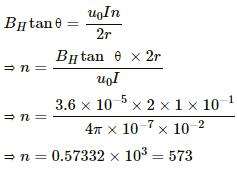
Q.17. A moving-coil galvanometer has a 50-turn coil of size 2 cm × 2 cm. It is suspended between the magnetic poles producing a magnetic field of 0.5 T. Find the torque on the coil due to the magnetic field when a current of 20 mA passes through it.
Given :
Number of turns in the coil, n = 50
Area of the cross section of the coil, A = 2 cm × 2 cm = 2 × 2 × 10−4 m2
Current flowing through the coil, I = 20 x 10-3 A
Magnetic field strength due to the presence of the poles, B = 0.5 T
The torque experienced by the coil placed in an external magnetic field (τ) is given by
Q.18. A short magnet produces a deflection of 37° in a deflection magnetometer in Tan-A position when placed at a separation of 10 cm from the needle. Find the ratio of the magnetic moment of the magnet to the earth's horizontal magnetic field.
Given :
Deflection in the magnetometer in the given position when placed in the magnetic field of a short magnet, θ = 37°
Separation between the magnet and the needle, d = 10 cm = 0.1 m
Let M be the magnetic moment of the magnet and BH be Earth's horizontal magnetic field.
According to the magnetometer theory,
For the short magnet ,
Q.19. The magnetometer of the previous problem is used with the same magnet in Tan-B position. Where should the magnet be placed to produce a 37° deflection of the needle?
Given:
Deflection in the magnetometer in the given position when placed in the magnetic field of a short magnet, θ = 37°
Separation between the magnet and the needle, d = 10 cm = 0.1 m
Let M be the magnetic moment of the magnet and BH be Earth's horizontal magnetic field.
According to the magnetometer theory,
For the short magnet ,
= 3.75 × 103 A-m2/T
Deflection in the magnetometer θ = 37°
From the magnetometer theory in Tan-B position, we have
Since for the short magnet / << d , we can neglect l w.r.t d.
Now,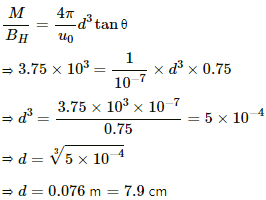
Magnet will be at 7.9 cm from the centre.
Q.20. A deflection magnetometer is placed with its arms in north-south direction. How and where should a short magnet having M/BH = 40 A m2 T−1 be placed so that the needle can stay in any position?
Given :
Ratio,
Since the magnet is short, l can be neglected.
So, using the formula for M/BH from the magnetometer theory and substituting all values, we get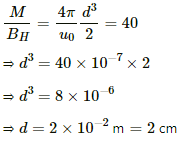
Thus, the magnet should be placed in such a way that its north pole points towards the south and it is 2 cm away from the needle.
Q.21. A bar magnet takes π/10 second the complete one oscillation in an oscillation magnetometer. The moment of inertia of the magnet about the axis of rotation is 1.2 × 10−4 kg m2 and the earth's horizontal magnetic field is 30 μT. Find the magnetic moment of the magnet.
Given :
Time taken by the bar magnet to complete one oscillation,
Moment of inertia of the magnet about the axis of rotation, I =
Horizontal component of Earth's magnetic field, BH = 30 μT
Time period of oscillating magnetometer (T) is given by
Here,
M = Magnetic moment of the magnet
On substituting the respective values, we get
Q.22. The combination of two bar magnets makes 10 oscillations per second in an oscillation magnetometer when like poles are tied together and 2 oscillations per second when unlike poles are tied together. Find the ratio of the magnetic moments of the magnets. Neglect any induced magnetism.
Given :
Number of oscillations per second made by the combination of bar magnets with like poles,
Number of oscillations per second made by the combination of bar magnets with unlike poles,
The frequency of oscillations in the magnetometer (V) is given by
When like poles are tied together, the effective magnetic moment is
When unlike poles are tied together, the effective magnetic moment is
As the frequency of oscillations is directly proportional to the magnetic moment ,
Hence, the ratio of the effective magnetic moment is -(13/12).
Q.23. A short magnet oscillates in an oscillation magnetometer with a time period of 0.10 s where the earth's horizontal magnetic field is 24 μT. A downward current of 18 A is established in a vertical wire placed 20 cm east of the magnet. Find the new time period.
Here,
Horizontal component of Earth's magnetic field, BH = 24 × 10−6 T
Time period of oscillation, T1 = 0.1 s
Downward current in the vertical wire, I = 18 A
Distance of wire from the magnet, r = 20 cm = 0.2 m
In the absence of the wire net magnetic field, BH = 24 × 10−6 T
When a current-carrying wire is placed near the magnet, the effective magnetic field gets changed.
Now the net magnetic field can be obtained by subtracting the magnetic field due to the wire from Earth's magnetic field.
Thus, the magnetic field due to the current-carrying wireis given by
The net magnetic field (B) is given by
Time period of the coil (T) is given by
Let T1 and T2 be the time periods of the coil in the absence of the wire and in the presence the wire respectively.
As time period is inversely proportional to magnetic field,
Q.24. A bar magnet makes 40 oscillations per minute in an oscillation magnetometer. An identical magnet is demagnetized completely and is placed over the magnet in the magnetometer. Find the time taken for 40 oscillations by this combination. Neglect any induced magnetism.
Given :
Frequency of oscillations of the bar magnet in the oscillation magnetometer, V = 40 min-1
Time period for which the bar magnet is placed in the oscillation magnetometer, T1 = 1/40 min
The time period of oscillations of the bar magnet (T) is given by
Here,
I = Moment of inertia
M = Magnetic moment of the bar magnet
BH = Horizontal component of the magnetic field
Now, let T2 be the time period for which the second demagnetised magnet is placed over the magnet.
As the second magnet is demagnetised, the combination will have the same values of Mand BH as those for the single magnet. However, variation will be there in the value of Ion placing the second demagnetised magnet.
For 1 oscillation,
Time taken = 0.03536 min
For 40 oscillations,
Time taken = 0.03536 × 40.
Q.25. A short magnet makes 40 oscillations per minute when used in an oscillation magnetometer at a place where the earth's horizontal magnetic field is 25 μT. Another short magnet of magnetic moment 1.6 A m2 is placed 20 cm east of the oscillating magnet. Find the new frequency of oscillation if the magnet has its north pole (a) towards north and (b) towards south.
Here,
Frequency of oscillations, V1 = 40 oscillations/min
Earth's horizontal magnetic field, BH = 25 μT
Magnetic moment of the second magnet, M = 1.6 A-m2
Distance at which another short magnet is placed, d = 20 cm = 0.2 m
(a) For the north pole of the short magnet facing the north, frequency (V1) is given by
Here,
M = Magnetic moment of the magnet
I = Moment of inertia
BH = Horizontal component of the magnetic field
Now, let B be the magnetic field due to the short magnet.
When the north pole of the second magnet faces the north pole of the first magnet, the effective magnetic field (Beff)is given by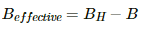
The new frequency of oscillations (V2) on placing the second magnet is given by
The magnetic field produced by the short magnet (B) is given by
Since the frequency is proportional to the magnetic field,
= 18 oscillations/min
(b) For the north pole facing the south,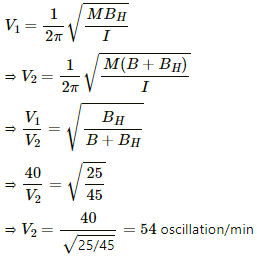
|
134 docs
|
FAQs on HC Verma Questions and Solutions: Chapter 36: Permanent Magnets- 2 - HC Verma Solutions - JEE
| 1. What are permanent magnets? |  |
| 2. How are permanent magnets different from temporary magnets? |  |
| 3. How are permanent magnets used in everyday life? |  |
| 4. Can the strength of a permanent magnet be increased? |  |
| 5. How can permanent magnets be demagnetized? |  |