Acceleration: At a glance | Physics for MCAT PDF Download
What is Acceleration?
In the realm of golf, one can find hidden lessons about acceleration and its significance. Imagine standing on a tee, preparing to strike the golf ball towards the distant flagpole. In this moment, a wise golf ball guru, who doubles as a physics teacher, imparts their wisdom. They reveal that the key to changing the ball's position is through displacement, the alteration of its position from one point to another. This newfound insight sparks curiosity about how to initiate such a change.
The Role of Velocity
As the golf ball rests motionless, your sensei explains that it requires velocity to set the ball in motion. Velocity represents the change in position over time, signifying how the ball's position evolves. Eager to impress, you strike the ball with your club, witnessing it soar through the air. The ball's movement demonstrates the alteration in position as time progresses, known as velocity.
Understanding Acceleration
To initiate a change in velocity, acceleration becomes paramount. Acceleration encompasses alterations in velocity over time, encompassing instances of speeding up, slowing down, or changing direction. Consider measuring the golf ball's velocity just before and after hitting it:
- Velocity before impact: 0 meters/second (m/s)
- Velocity 0.2 seconds after impact: 15 m/s
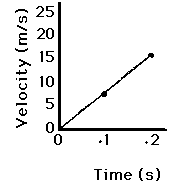
Using the equation a = Δv/Δt (where 'a' represents average acceleration, 'v' denotes velocity, and 't' signifies time), we can describe acceleration as the change in velocity over time. Thus, the average acceleration in this scenario is calculated as 75 m/s2.
The Dance of Distance, Time, Acceleration, and Velocity
Although our golf ball does not possess rocket propulsion, we discover that continuous acceleration is not feasible. Unless external forces act upon it, the ball will ultimately maintain a constant velocity, represented by a horizontal line on a graph. However, if we transition from golf to automobiles, acceleration's principles remain unchanged.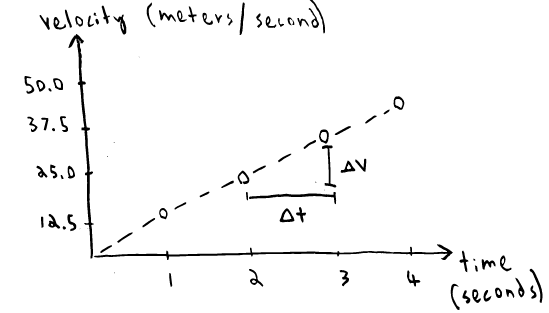
Acceleration in the Context of a Car
Imagine a car starting from rest and accelerating to 50 m/s in a straight line. Graphing the car's change in speed against time reveals a steadily increasing velocity, illustrating the presence of acceleration. By analyzing the slope of this graph, we determine the magnitude of the acceleration. A steeper slope signifies a greater acceleration, while a downward bend indicates negative acceleration or deceleration. Negative acceleration implies transitioning from a higher to a lower velocity, not necessarily moving backward.
 |
Download the notes
Acceleration: At a glance
|
Download as PDF |
Real-Life Application of Formulas
How can we calculate the displacement of a car during a specific period of acceleration? Utilizing the formula d = (1/2)at² + v₀t, we can ascertain the car's distance traveled. In this equation, 'd' represents displacement, 'a' denotes acceleration, 't' signifies time, and 'v₀' indicates initial velocity. If the car begins from rest, the initial velocity 'v₀' can be set to zero.
Unraveling Complex Scenarios
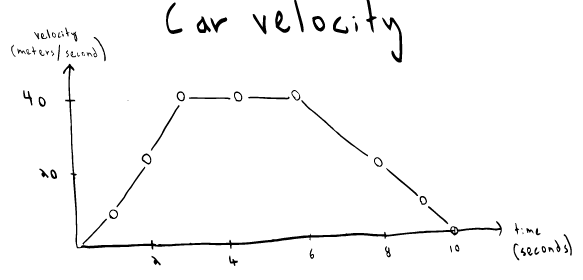
What if our journey involves varying rates of acceleration? Let's consider a scenario where a car accelerates to 40 m/s in 3 seconds, maintains that velocity for another 3 seconds, and then decelerates to zero over 4 seconds. By analyzing the graph of velocities over time, we can divide the area beneath the curve into triangles and a rectangle. Summing the areas allows us to determine the total distance traveled by the car during this 10-second period.
Analyzing the graph, we divide it into three sections based on the different stages of acceleration and deceleration:
Section 1: Acceleration from rest to 40 m/s in 3 seconds.
- Using the formula d = (1/2)at2 + v₀t, we can calculate the displacement during this stage.
- With an initial velocity (v₀) of 0 m/s, the acceleration (a) is obtained by dividing the change in velocity (40 m/s - 0 m/s) by the time (3 seconds).
- Plugging in the values, we find the displacement in this section to be (1/2)(40 m/s2)(3 seconds)2 = 180 meters.
Section 2: Constant velocity of 40 m/s for 3 seconds.
- As the velocity remains constant, there is no acceleration, and therefore, the displacement can be found using the formula d = vt.
- Since the velocity (v) is 40 m/s and the time (t) is 3 seconds, the displacement in this section is (40 m/s)(3 seconds) = 120 meters.
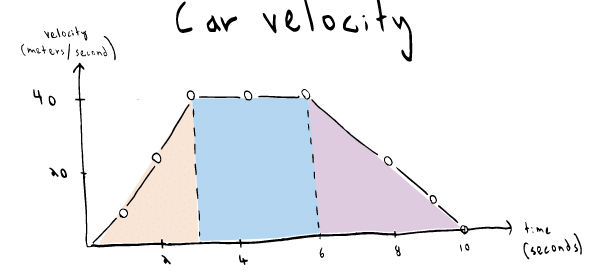
Section 3: Deceleration from 40 m/s to rest in 4 seconds.
- The car is decelerating, so the acceleration is negative. We can calculate the acceleration using the formula a = Δv/Δt, where the change in velocity (Δv) is -40 m/s (final velocity - initial velocity) and the time (Δt) is 4 seconds.
- Plugging in the values, we find the acceleration to be (-40 m/s)/4 seconds = -10 m/s2.
- Using the formula d = (1/2)at2 + v₀t, we can calculate the displacement during deceleration.
- Since the initial velocity (v₀) is 40 m/s, the acceleration (a) is -10 m/s2, and the time (t) is 4 seconds, the displacement in this section is (1/2)(-10 m/s2)(4 seconds)2 + (40 m/s)(4 seconds) = -80 meters.
To find the total distance traveled, we sum the displacements from each section: 180 meters + 120 meters - 80 meters = 220 meters. Therefore, during the 10-second period, the car traveled a total distance of 220 meters.
Conclusion
From the golf ball's journey to the intricacies of car physics, acceleration emerges as a crucial force driving change. Whether it's launching a golf ball towards the green or accelerating a car on the road, understanding acceleration allows us to comprehend the dynamics of motion. By unraveling the principles of acceleration and utilizing formulas to analyze complex scenarios, we can unlock a deeper understanding of the physical world around us. So, let's embrace the fascinating dance between distance, time, acceleration, and velocity, and embark on a journey of exploration and discovery.
|
158 videos|9 docs|21 tests
|





















