Profit, Loss & Discount | Mathematics for JAMB PDF Download
| Table of contents |

|
| Introduction |

|
| Profit, Loss, and Discount |

|
| Profit and Loss Common Formulas |

|
| Profit and Loss Tricks |

|
| Some Solved Problems |

|
Introduction
- The profit and Loss formula is used in mathematics to determine the price of a commodity in the market and understand how profitable a business is.
- Every product has a cost price and a selling price.
- Based on the values of these prices, we can calculate the profit gained or the loss incurred for a particular product.
Profit, Loss, and Discount
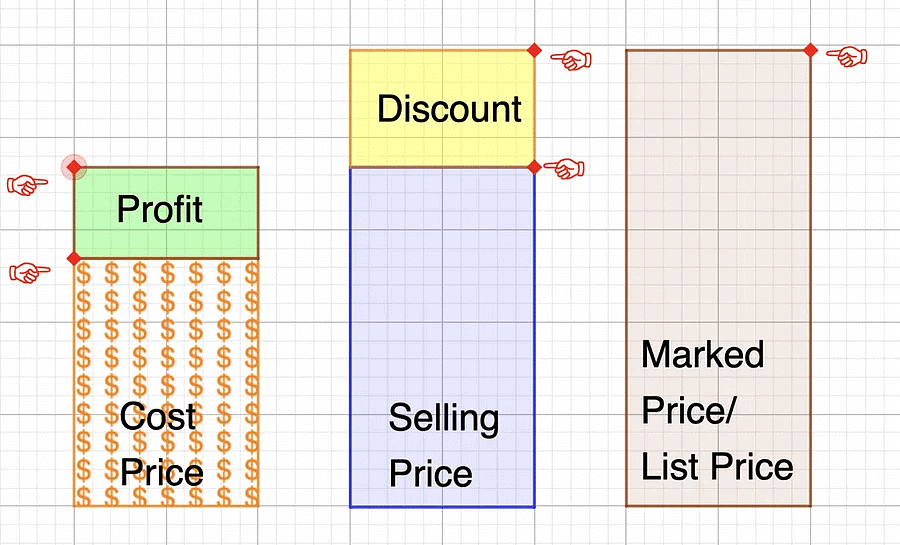
1. Cost Price (CP)
The amount paid for a product or commodity to purchase it is called a cost price. Also, denoted as CP.
This cost price is further classified into two different categories:
- Fixed Cost: The fixed cost is constant, it doesn’t vary under any circumstances
- Variable Cost: It could vary depending as per the number of units
2. Selling price (SP)
- The amount for which the product is sold is called Selling Price. It is usually denoted as SP. Also, sometimes called a sale price.
 |
Test: Profit and Loss - 1
|
Start Test |
3. Profit and Loss
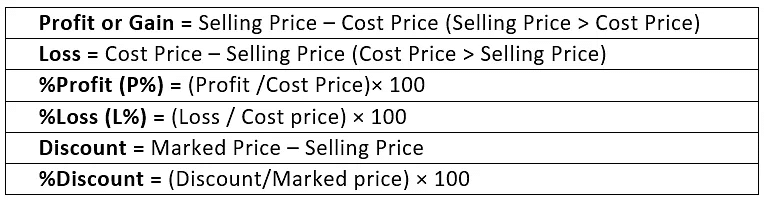
Profit: When an article is sold for more than the cost of the article, then we say there is a Profit or Gain.
- Profit or Gain = S.P - C.P
Loss: When an article is sold for less than the cost of the article, then we say there is a Loss.
- Loss = C.P - S.P
The formula for the profit and loss percentage is:
- Profit percentage = (Profit / Cost Price) x 100
- Loss percentage = (Loss / Cost price) x 100
4. Marked Price Formula (MP)
This is basically labeled by shopkeepers to offer a discount to the customers in such a way that,
- Discount = Marked Price – Selling Price
- Discount Percentage = (Discount/Marked price) x 100
Profit and Loss Common Formulas
You have learned until now how to calculate profit as well as loss and also the percentage of them. Here is a list of the most commonly used formulas for all related questions:
Profit and Loss Tricks
Now let us look at some additional tricks or formulas that can be used to solve maths problems based on gain and loss:
- SP = {(100 + P%)/100} x CP
- SP = {(100 – L%)/100} x CP
- CP = {100/(100 + P%)} x SP
- CP = {100/(100 – L%)} x SP
- SP = MP - Discount
- For false weight, profit percentage will be P% = (True weight – false weight/ false weight) x 100.
- When there are two successful profits say m% and n%, then the net percentage profit equals to (m+n+mn)/100
- When the profit is m% and loss is n%, then the net % profit or loss will be: (m-n-mn)/100
- If a product is sold at m% profit and then again sold at n% profit then the actual cost price of the product will be: CP = [100 x 100 x P/(100+m)(100+n)].
In case of loss, CP = [100 x 100 x P/(100-m)(100-n)] - If P% and L% are equal then, P = L and %loss = P2/100
 |
Download the notes
Profit, Loss & Discount
|
Download as PDF |
Some Solved Problems
Q1: A trader bought a pair of shoes for ₦5,000 and sold it for ₦6,500. What is the profit percentage?
(a) 10%
(b) 20%
(c) 25%
(d) 30%
Ans: (c)
The profit made by the trader is ₦6,500 - ₦5,000 = ₦1,500.
The profit percentage is calculated as (Profit/Cost Price) × 100%.
So, (1500/5000) × 100%
= 30%.
Therefore, the correct option is c) 25%.
Q2: A shopkeeper marked the price of a shirt as ₦1,200. He then offered a discount of 20% and sold it. How much did the customer pay?
(a) ₦800
(b) ₦960
(c) ₦1,000
(d) ₦1,440
Ans: (b)
The discount offered is 20% of ₦1,200, which is (20/100) × 1200 = ₦240.
The selling price after the discount is ₦1,200 - ₦240
= ₦960.
Therefore, the correct option is b) ₦960.
Q3: A car is sold at a profit of 15% for ₦345,000. What was its cost price?
(a) ₦300,000
(b) ₦295,650
(c) ₦300,250
(d) ₦310,250
Ans: (b)
Let the cost price of the car be x. The selling price is 115% of the cost price.
So, 115% of x is ₦345,000. This can be written as (115/100) × x
= ₦345,000. Solving for x gives x
= ₦345,000 × (100/115)
= ₦295,650.
Therefore, the correct option is b) ₦295,650.
Q4: A trader incurs a loss of 12% while selling a product for ₦4,400. What was the cost price of the product?
(a) ₦4,860
(b) ₦5,000
(c) ₦5,400
(d) ₦5,600
Ans: (c)
Let the cost price of the product be x. The selling price is 88% of the cost price.
So, 88% of x is ₦4,400.
This can be written as (88/100) × x = ₦4,400.
Solving for x gives x = ₦4,400 × (100/88)
= ₦5,400.
Therefore, the correct option is c) ₦5,400.
Q5: A laptop is sold at a loss of 20%. If the selling price is ₦32,000, what was the cost price of the laptop?
(a) ₦35,000
(b) ₦36,000
(c) ₦40,000
(d) ₦42,500
Ans: (d)
Let the cost price of the laptop be x. The selling price is 80% of the cost price (since it is sold at a loss of 20%). So, 80% of x is ₦32,000. This can be written as (80/100) × x = ₦32,000. Solving for x gives x = ₦32,000 × (100/80) = ₦40,000. Therefore, the correct option is d) ₦42,500.
|
139 videos|82 docs|101 tests
|















