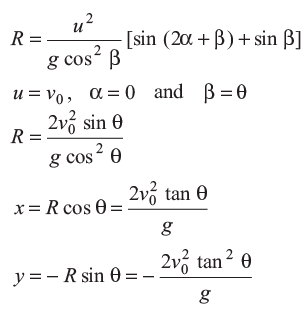Projectile Motion along an Inclined Plane

Up the Plane

In this case direction x is chosen up the plane and direction y is chosen perpendicular to the plane.
Hence,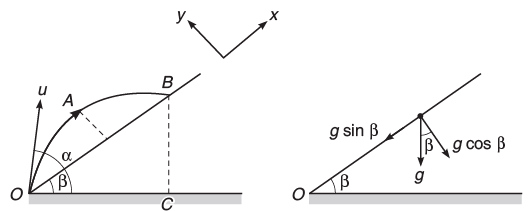

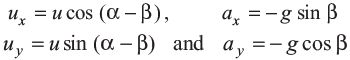
Now, let us derive the expressions for time of flight (T) and range (R) along the plane.

Time of Flight

At point B displacement along y-direction is zero. So, substituting the proper values in
s_y = u_yt + 1/2 α_yt², we get
0 = ut sin (α - β) + 1/2 (- g cos β)t² 
⇒ ∴ t = 0 and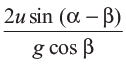

t = 0, corresponds to point O and t = 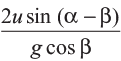corresponds to point B. Thus,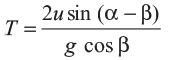

Note: Substituting β = 0, in the above expression, we get T = 2u sin α/g which is quite obvious because β = 0 is the situation shown in Fig.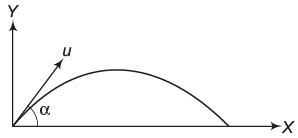

Range

Range (R) or the distance OB can be found by following two methods:
Method 1: Horizontal component of initial velocity is
u_H = u cos α
∴ OC = u_HT (as αH = 0)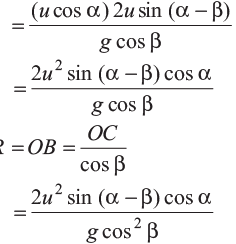


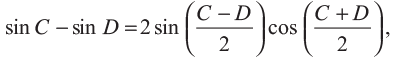
Range can also be written as,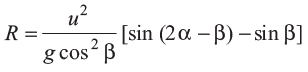

This range will be maximum when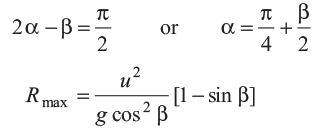

Here, also we can see that for β = 0, range is maximum at α = π/4 or α = 45°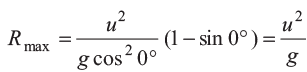

Method 2:
Range (R) or the distance OB is also equal to the displacement of projectile along x-direction in time t = T . Therefore,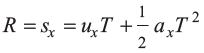

Substituting the values of u_x, α_x and T, we get the same result.
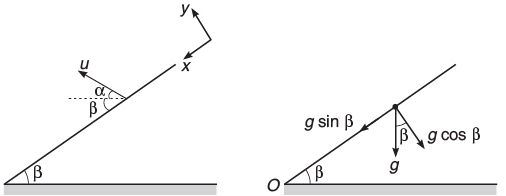
(ii) Down the Plane Here, x and y-directions are down the plane and perpendicular to plane respectively as shown in Fig. Hence,
u_x = u cos (α + β), = α_x = g sin β
u_y = u sin (α + β), = α_y = -g cos β
Proceeding in the similar manner, we get the following results: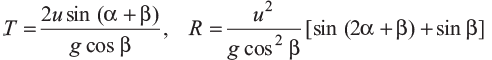

From the above expressions, we can see that if we replace β by -β, the equations of T and R for up the plane and down the plane are interchanged provided α (angle of projection) in both the cases is measured from the horizontal not from the plane.

Example: A man standing on a hill top projects a stone horizontally with speed v₀ as shown in figure. Taking the co-ordinate system as given in the figure. Find the co-ordinates of the point where the stone will hit the hill surface.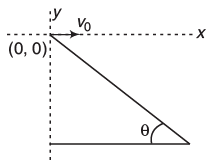

Range of the projectile on an inclined plane (down the plane) is,