Tips and Tricks: Subtraction | Improve Your Calculations: Vedic Maths (English) - Class 6 PDF Download
The Concept of Base
Sutra: All from 9 and the Last from 10
Numbers made up of only 1’s and 0’s are known as a Base.
Examples of a Base are
10, 100, 1000, 1, .01….etc
The base method is used for subtracting, multiplying or dividing numbers. Like 98, 898, 78999 etc that are close to base.
Applying the formula “All form 9 and Last form 10” to any number especially the big one’s reduces it to its smaller Counterpart that can be easily used for calculations involving the big digits like 7, 8, and 9.
Applying the formula “All from 9 and the last from 10”
Example: Apply ‘All from 9 Last from 10’ to
Subtract 789 from 1000
7 8 9
↓ ↓ ↓ [Here all from 9 last from 10 means subtract 78 8 from 9 and 9 from 10, so we get 211]
2 1 1
We get 211, because we take 7 and 8 from 9 and 9 from 10.
from 10000 from 100 from 100 from 100000
2772 54 97 10804
↓↓↓↓ ↓↓ ↓↓ ↓↓↓↓↓
7228 46 03 89196
If you look carefully at the pairs of numbers in the above numbers you may notice that in every case the total of two numbers is a base number 10, 100, 1000 etc.
This gives us an easy way to subtract from base numbers like 10, 100, 1000…….
Subtracting from a Base
Example: 1000 – 784 = 216
Just apply ‘All from 9 and the Last from 10’ to 784, difference of 7 from 9 is 2, 8 from 9 is 1, 4 from 10 is 6 so we get 216 after subtraction.
When subtracting a number from a power of 10 subtract all digits from 9 and last from 10.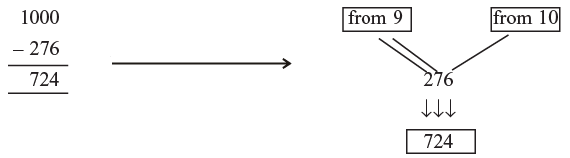
Subtracting from a Multiple of a Base
Sutra: ‘All from 9 and the last from 10’
and
‘One less than the one before’
Example: 600 – 87
We have 600 instead of 100. The 6 is reduced by one to 5, and the All from 9 and last from 10 is applied to 87 to give 13. Infact, 87 will come from one of those six hundred, so that 500 will be left.
∴ 600 – 87 = 513 [Note: First subtract form 100 then add 500, as 500 + 13 = 513]
Example: Find 5000 – 234
5, is reduced to one to get 4 and the formula converts 234 to 766
∴ 5000 - 234 = 4766
Example: 1000 – 408 = 592
Example: 100 – 89 = 11
Example: 1000 – 470 = 530 [Remember apply the formula just to 47 here.]
If the number ends in zero, use the last non-zero number non-zero number as the last number for example.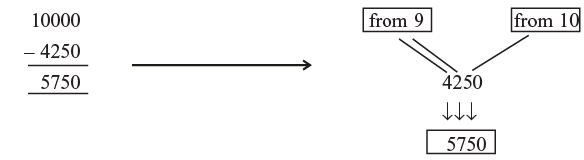 Hence 1000 – 4250 = 5750
Hence 1000 – 4250 = 5750
Adding Zeroes
In all the above sums you may have noticed that the number of zeros in the first number is the same as the numbers of digits in the number being subtracted.
Example: 1000 – 53 here 1000 has 3 zeros and 53 has two digits.
We can solve this by writing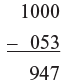
We put on the extra zero in front of 53 and then apply the formula to 053.
Example: 10000 – 68, Here we need to add two zeros.
10000 – 0068 = 9932
Example: Find 9000 – 5432
Sutra: ‘One more than the previous one’ and ‘all from 9 and the Last from the 10’
Considering the thousands 9 will be reduced by 6 (one more than 5) because we are taking more than 5 thousand away
‘All from 9 and the last from 10’ is than applied to 432 to give 568
9000 – 5432 = 3568
Similarly—7000 – 3884
= 3116 {3 = 7 – 4, 4 is one more than 3 and 116 = 4000 – 3884} by all from a and the last from 10}
If the number is less digits, then append zero the start: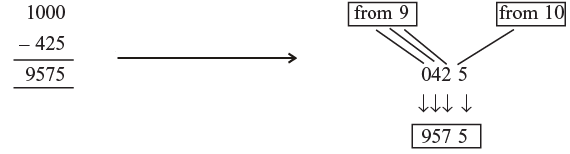
When subtracting form a multiple of a power of 10, just decrement the first digit by 1, then subtract remaining digits:

Look at one more example:
Money: A great application of "all from 9 and last from 10" is money. Change can be calculated by applying this sutra mentally for example: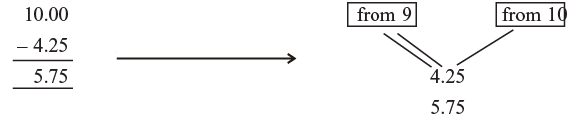
This is helpful because most our rupee notes are multiple of 10's.
Subtracting Near a base
Rule: By completion or non-completion.
when subtracting a number close to a multiple of 10. Just subtract from the multiple of 10 and correct the answer accordingly.
Example: 53 – 29
29 is just close to 30, just 1 short, so subtract 30 from 53 making 23, then add 1 to make 24.
53 – 29 = 53 – 30 + 1
= 23 + 1
= 24
Similarly
45 – 18
= 45 – 20 + 2
= 25 + 2
= 27 {18 is near to 20, just 2 short)
Use the base method of calculating
To find balance
Q1: Suppose you buy a vegetable for Rs. 8.53 and you buy with a Rs. 10 note. How much change would you expect to get?
Ans: You just apply “All from 9 and the last from 10” to 853 to get 1.47.
Q2: What change would expect from Rs. 20 when paying Rs. 2.56?
Ans: The change you expect to get is Rs. 17.44 because Rs. 2.56 from Rs.10 is Rs. 7.44 and there is Rs. 10 to add to this.
Subtracting number just below the base
Example: find 55 – 29
Subtraction of numbers using "complete the whole"
Step 1: 20 is the sub base close to 19
19 is 1 below 20
Step 2: take 20 from 55 (to get 35)
Step 3: Add 1 back on 55 – 19 = 36
Example: 61 – 38
38 is near to 40 = 40 – 38 = 2
61 – 40 = 21
61 – 38 = 21 + 2 = 23
Example: 44 – 19
19 + 1 = 20
44 – 20 = 24
44 – 19 = 24 – 1 = 23
Example: 88 – 49
49 + 1 = 50
88 – 50 = 38
88 – 49 = 38 + 1 = 39
Example: 55 – 17
17 + 3 = 20
55 – 20 = 35
55 – 17 = 35 + 3 = 38
Number splitting Method
As you have use this method in addition the same can be done for subtraction also: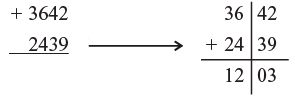 Note: The split allows on to add '36 – 24' and 42 – 39 both of which can be done mentally
Note: The split allows on to add '36 – 24' and 42 – 39 both of which can be done mentally
General Method of Subtraction
Subtraction from left to right
In this section we show a very easy method of subtracting numbers from left to right that we have probably not seen before. We start from the left, subtract, and write it down if the subtraction in the next column can be done. If it cannot be done you put down one less and carry 1, and then subtract in the second column.
Example: Find: 83 – 37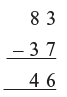
Find: 78 – 56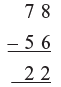
Left to right
(1)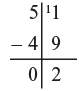
(2)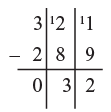
(3)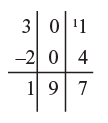
(4)
(5)
Starting from the left we subtract in each column 3 - 1 = 2 but before we put 2 down we check that in next column the top number is larger. In this case 5 is larger than 1 so we put 2 down.
In the next column we have 5 - 1 = 4, but looking in the third column we see the top number is not larger than the bottom( 5 is less than 8) so instead putting 4 down we put 3 and the other 1 is placed as the flag, as shown so that 5 becomes 15, so now we have 15 - 8 = 7. Checking in the next column we can put this down because 6 is greater than 2. In the fourth column we have 6 - 2 = 4, but looking at the next column (7 is smaller than 8) we put down only 3 and put the other flag with 7 as shown finally in the last column 17 - 8 = 9.
|
38 videos|31 docs|9 tests
|





















