| Table of contents |

|
| Angle Measurements |

|
| Measure an Angle in Sexagecimal System (Degree, Minute, Second) |

|
| Measure an Angle in Circular System (Radians) |

|
| Relationship Between Radians and Degrees |

|
Angle Measurements
We define an angle as the union of two non-collinear rays that have a common starting point. The two rays are referred to as the arms of the angle and the common starting point is called its vertex.
We can interpret an angle by rotating a ray from one position to another. When we use this interpretation of an angle, the ray to begin with is called the initial side, and the final position of ray is called the terminal sideasshown in the figure.
If we rotate the ray in anti-clockwise direction, the angle formed in this way is termed as positive angle. The angle formed by clockwise rotation of ray is termed as negative angle.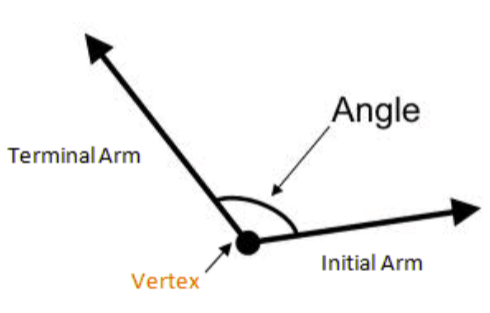
Angles are commonly measured in two methods: Degrees & Radians. We discuss both these methods one-by-one.
Measure an Angle in Sexagecimal System (Degree, Minute, Second)
In this method, we measure an angle in terms of degrees, minutes and seconds. We divide the circumference of a circle into 360 equal arcs. The angle subtended at the centre of the circle by one arc is called one degree and is denoted be 1o (The small circle is a symbol for degree). Similarly 1' denotes a minute and 1'' denotes a second in sexagecimal system of angle measurement.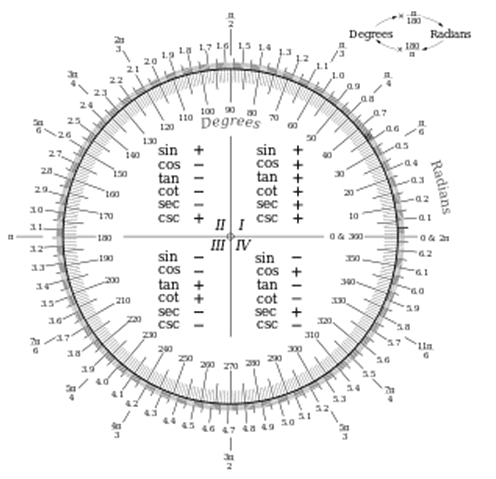
The following equations show the relationships of degree, minute and second with each other.
1 minute = 60 seconds (60'')
1 degree = 60 minutes (60')
One complete revolution = 360o
We present a few examples for conversion of an angle given in Sexagecimal form into decimal form and vice versa.
Example: Convert 45o30' into decimal degrees.
Solution: 45o 30' = 45o + (30/60) = 45o + 0.5o = 45.5o
Since, (1/60 degree = 1 minute )
Measure an Angle in Circular System (Radians)
''A radian is the measure of an angle subtended at the centre of a circle by an arc whose length is equal to the radius of that circle.''
The angle m∠ XOY in the figure is one radian since the length of the arc XY is equal to the radius of the circle. => m∠ XOY = 1 radian
Note: The length ''l'' of an arc that subtends an angle θ at the center of a circle of radius r is given by l = rθ
i.e. Arc length is angle times radius of the circle. (Here θ is in radians, not in degrees)
Relationship Between Radians and Degrees
We know that for a circle of radius r, the circumference C of the circle is given by C=2π r. Since, l(Arc length) = rθ ......................... (i)
Also l =2π r for a complete Circle of radius r ..................... (ii)
⇒ 2π r = rθ
⇒ θ = 2π r / r = 2π radians
We know that for a complete revolution, the angle measure in degrees is 360o
⇒ 2π radians = 360o
⇒ π radians = 180o
⇒ 1 radian = 180o / π = 57.296o
1 radian =57.296o
Also 1o = π / 180 radians = 0.0175 radians
1 degree = 0.0175 rad
Example: Convert 30o into radian measure of angles.
Solution: We know that 1o π/180 radians
⇒ 30o = 30 x π/180 radians
⇒ 30o = π/6 radians

|
Explore Courses for JEE exam
|

|
















