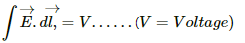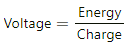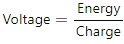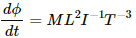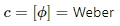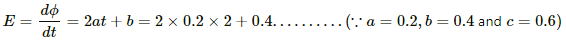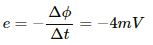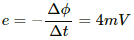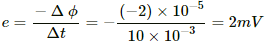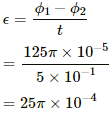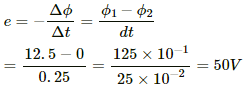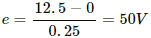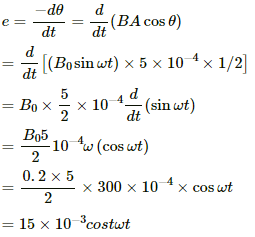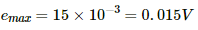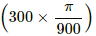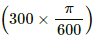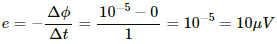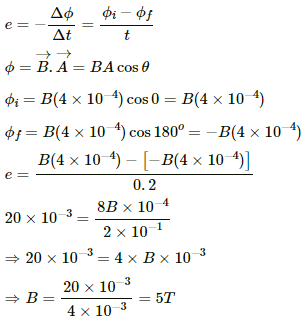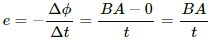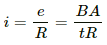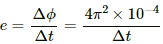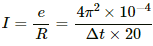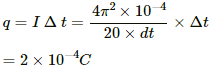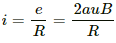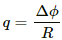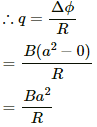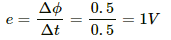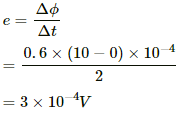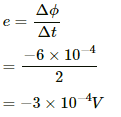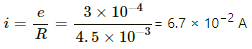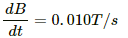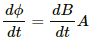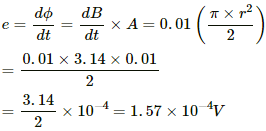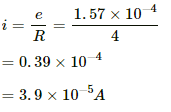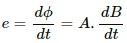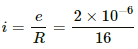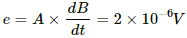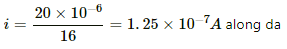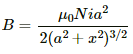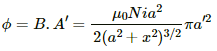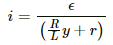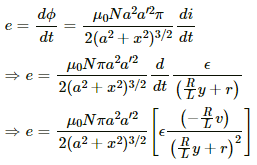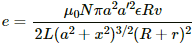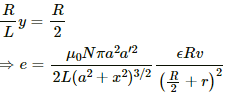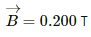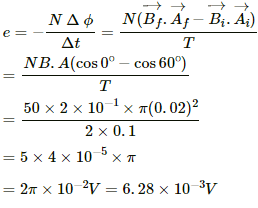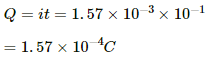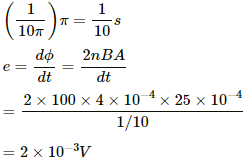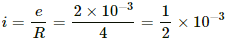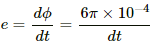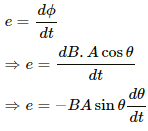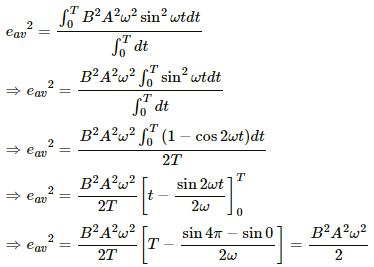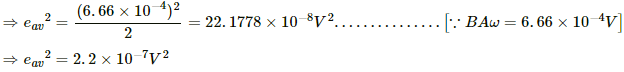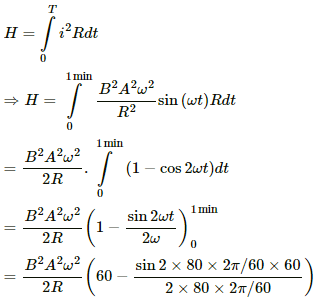HC Verma Questions and Solutions: Chapter 38: Electromagnetic Induction- 2 | HC Verma Solutions - JEE PDF Download
Exercises
Q.1. Calculate the dimensions of (a) 
(b) vBl and (c) 
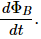The symbols have their usual meaning.
(a) The quantity
can also be written as :-
Unit of voltage is J/C.
Voltage can be written as:-
Dimensions of energy = [ML2T-2]
Dimensions of charge = [IT]
Thus, the dimensions of voltage can be written as:
[ML2T-2] ×[IT]−1 = [ML2I−1T−3]
(b) The quantity vBl is the product of quantities v, B and L.
Dimensions of velocity v = [LT−1]
Dimensions of length l = [L]
The dimensions of magnetic field B can be found using the following formula:-
B = F/qv
Dimensions of force F = [MLT−2]
Dimensions of charge q = [IT]
Dimensions of velocity = [LT−1]
The dimensions of a magnetic field can be written as:
MI−1T−2
∴ Dimensions of vBl = [LT−1] × [MI−1T−2] × [L]= [ML2I−1T−3]
(c) The quantity
Voltage can be written as:-
Dimensions of energy = [ML2T-2]
Dimensions of charge = [IT]
The dimensions of voltage can be written as:
[ML2T-2] ×[IT]−1 = [ML2I−1T−3]
∴ Dimensions of
can also be written as :-
is equal to the emf induced; thus, its dimensions are the same as that of the voltage.
Q.2. The flux of magnetic field through a closed conducting loop changes with time according to the equation, Φ = at2 + bt + c. (a) Write the SI units of a, b and c. (b) If the magnitudes of a, b and c are 0.20, 0.40 and 0.60 respectively, find the induced emf at t = 2 s.
According to the principle of homogeneity of dimensions, the dimensions of each term on both the sides of a correct equation must be the same.
Now,
ϕ = at2 + bt + c
(a) The dimensions of the quantities at2, bt, c and ϕ must be the same.
Thus, the units of the quantities are as follows:-
(b) The emf is written as:-
On substituting t = 2 s, we get
E = 0.8 + 0.4 = 1.2 V
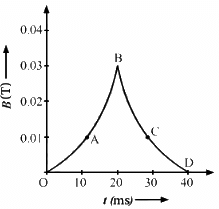
Q.3. (a) The magnetic field in a region varies as shown in figure. Calculate the average induced emf in a conducting loop of area 2.0 × 10−3 m2 placed perpendicular to the field in each of the 10 ms intervals shown. (b) In which intervals is the emf not constant? Neglect the behaviour near the ends of 10 ms intervals.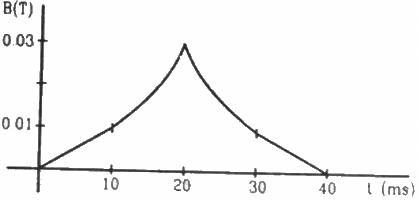
Given:-
Area of the loop = 2.0 × 10−3 m2
The following conclusions can be made from the graph given above:
The magnetic flux at point O is 0.
The magnetic flux at point A is given by
ϕ2 = B.A = 0.01 × 2 × 10−3
= 2 × 10−5 ............[∵ ϕ1 = 0]
The change in the magnetic flux in 10 ms is given by
Δϕ = 2 × 10−5
The emf induced is given by
The magnetic flux at point B is given by
ϕ3 = B.A = 0.03 × 2 × 10−3
= 6 × 10−5
The change in the magnetic flux in 10 ms is given by
Δϕ = 6 × 10−5 − 2 × 10−5 = 4 × 10−5
The emf induced is given by
The magnetic flux at point C is given by
ϕ4 = B.A = 0.01 × 2 × 10−3
= 2 × 10−5
The change in the magnetic flux in 10 ms is given by
Δϕ = (2 × 10−5 − 6 × 10−5 ) = − 4 × 10−5
The emf induced is given by
The magnetic flux at point D is given by
ϕ5 = B.A = 0
The change in the magnetic flux in 10 ms is given by
Δϕ = 0 − 2 × 10−5
The emf induced is given by
(b) Emf is not constant in the intervals 10 ms‒20 ms and 20 ms‒30 ms.
Q.4. A conducting circular loop having a radius of 5.0 cm, is placed perpendicular to a magnetic field of 0.50 T. It is removed from the field in 0.50 s. Find the average emf produced in the loop during this time.
Given:-
Magnetic field intensity, B = 0.50 T
Radius of the loop, r = 5.0 cm = 5 × 10−2 m
∴ Area of the loop, A = πr2
Initial magnetic flux in the loop, ϕ1 = B × A
ϕ1 = 0.5 × π(5 × 10−2)2 = 125π × 10−5
As the loop is removed from the magnetic field, magnetic flux (ϕ2) = 0.
Induced emf ε is given by
= 25 × 3.14 × 10−4
= 78.5 × 10−4 V = 7.8 × 10−3 V
Q.5. A conducting circular loop of area 1 mm2 is placed coplanarly with a long, straight wire at a distance of 20 cm from it. The straight wire carries an electric current which changes from 10 A to zero in 0.1 s. Find the average emf induced in the loop in 0.1 s.
Given:-
Area of the loop, A = 1 mm2
Current through the wire, i = 10 A
Separation between the wire and the loop, d = 20 cm
Time, dt = 0.1 s
The average emf induced in the loop is given by
Q.6. A square-shaped copper coil has edges of length 50 cm and contains 50 turns. It is placed perpendicular to a 1.0 T magnetic field. It is removed from the magnetic field in 0.25 s and restored in its original place in the next 0.25 s. Find the magnitude of the average emf induced in the loop during (a) its removal, (b) its restoration and (c) its motion.
(a) When the coil is removed from the magnetic field:-
Initial magnetic flux through the coil, ϕ1 = BA
∴ ϕ1 = 50 × 0.5 × 0.5 T-m2
= 12.5 T-m2
Now,
Initial magnetic flux through the coil, ϕ2 = 0
Time taken, t = 0.25 s
The average emf induced is given by
(b) When the coil is taken back to its original position:-
Initial magnetic flux through the coil, ϕ1 = 0
Initial magnetic flux through the coil, ϕ2 = 12.5 T-m2
Time taken, t = 0.25 s
The average emf induced is given by
(c) When the coil is moving outside the magnetic field:-
Initial magnetic flux, ϕ1 = 0
Final magnetic flux, ϕ2 = 0
Because there is no change in the magnetic flux, no emf is induced.
Q.7. Suppose the resistance of the coil in the previous problem is 25Ω. Assume that the coil moves with uniform velocity during its removal and restoration. Find the thermal energy developed in the coil during (a) its removal, (b) its restoration and (c) its motion.
Given:-
Resistance of the coil, R = 25 Ω
(a) During the removal the emf induced in the coil,
e = 50 V
time taken, t = 0.25 s
current in the coil,
i = e/R = 2A
Thus, the thermal energy developed is given by
H = I2RT
= 4 × 25 × 0.25 = 25 J
(b) During the restoration of the coil,
emf induced in it, e = 50 V
time taken, t = 0.25 s
current in the coil,
i = e/R = 2A
Thus, the thermal energy developed is given by
H = i2RT = 25 J
(c) We know that energy is a scalar quantity. Also, the net thermal energy is the algebraic sum of the two energies calculated.
∴ Net thermal energy developed
= 25 J + 25 J = 50 J
Q.8. A conducting loop of area 5.0 cm2 is placed in a magnetic field which varies sinusoidally with time as B = B0 sin ωt where B0 = 0.20 T and ω = 300 s−1. The normal to the coil makes an angle of 60° with the field. Find (a) the maximum emf induced in the coil, (b) the emf induced at τ = (π/900)s and (c) the emf induced at t = (π/600) s.
Given:-
Area of the coil, A = 5 cm2 = 5 × 10−4 m2
The magnetic field at time t is given by
B = B0 sin ωt = 0.2 sin (300t)
Angle of the normal of the coil with the magnetic field, θ = 60°
(a) The emf induced in the coil is given by
The induced emf becomes maximum when cos ωt becomes maximum, that is, 1.
Thus, the maximum value of the induced emf is given by
(b) The induced emf at t =
e = 15 × 10−3 × cos ωt
= 15 × 10−3 × cos
= 15 × 10−3 × 1/2
(c) The induced emf at t = (π/600) s is given by
e = 15 × 10−3 × cos
= 15 × 10−3 × 0 = 0 V
is given by
Q.9. Figure shows a conducting square loop placed parallel to the pole-faces of a ring magnet. The pole-faces have an area of 1 cm2 each and the field between the poles is 0.10 T. The wires making the loop are all outside the magnetic field. If the magnet is removed in 1.0 s, what is the average emf induced in the loop?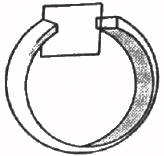
It is given that the magnitude of the magnetic field is 0.10 T and it is perpendicular to the area of the loop.
Also,
Area of the loop, A = 1 cm2 = 10−4 m
Time taken to remove the magnet completely, T = 2 s
Initial magnetic flux, ϕ =
Now, the induced emf in the magnetic field is given by
= BA cos(0) = 10−1 × 10−4 × 1 = 10−5
Q.10. A conducting square loop having edges of length 2.0 cm is rotated through 180° about a diagonal in 0.20 s. A magnetic field B exists in the region which is perpendicular to the loop in its initial position. If the average induced emf during the rotation is 20 mV, find the magnitude of the magnetic field.
Given:-
Induced emf, e = 20 mV = 20 × 10−3 V
Area of the loop, A = (2 × 10−2)2 = 4 × 10−4 m2
Time taken to rotate the loop, Δt = 0.2 s
The average induced emf is given by
Q.11. A conducting loop of face-area A and resistance R is placed perpendicular to a magnetic field B. The loop is withdrawn completely from the field. Find the charge which flows through any cross-section of the wire in the process. Note that it is independent of the shape of the loop as well as the way it is withdrawn.
The magnetic flux through the coil is given by
ϕ = B.A = BA cos 0° = BA
It is given that the loop is withdrawn from the magnetic field.
∴ Final flux = 0
The average induced emf is given by
The current in the loop is given by
The charge flowing through the area of the cross section of the wire is given by q = it = BA/R
Q.12. A long solenoid of radius 2 cm has 100 turns/cm and carries a current of 5 A. A coil of radius 1 cm having 100 turns and a total resistance of 20 Ω is placed inside the solenoid coaxially. The coil is connected to a galvanometer. If the current in the solenoid is reversed in direction, find the charge flown through the galvanometer.
Given:-
Radius of the solenoid, r = 2 cm = 2 × 10−2 m
Number of turns per centimetre, n = 100 = 10000 turns/m
Current flowing through the coil, i = 5 A
The magnetic field through the solenoid is given by
B = μ0ni = 4π × 10−7 × 10000 × 5
= 20π × 10−3 T
Flux linking with per turn of the second solenoid = Bπr2 = Bπ × 10−4
Total flux linking the second coil, ϕ1 = Bn2πr2
∴ ϕ1 = 100 × π × 10−4 × 20π × 10−3
When the direction of the current is reversed, the total flux linking the second coil is given by
ϕ2 = −Bn2πr2
= −(100 × π × 10−4 × 20π × 10−3 )
The change in the flux through the second coil is given by
Δϕ = ϕ2 − ϕ1
= 2 × (100 × π × 10−4 × 20π × 10−3)
Now,
The current through the solenoid is given by
The charge flown through the galvanometer is given by
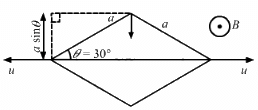
Q.13. Figure shows a metallic square frame of edge a in a vertical plane. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the figure. Two boys pull the opposite corners of the square to deform it into a rhombus. They start pulling the corners at t = 0 and displace the corners at a uniform speed u. (a) Find the induced emf in the frame at the instant when the angles at these corners reduce to 60°. (b) Find the induced current in the frame at this instant if the total resistance of the frame is R. (c) Find the total charge which flows through a side of the frame by the time the square is deformed into a straight line.
(a) The effective length of each side is the length that is perpendicular to the velocity of the corners.
Thus, the effective length of each side is a sin θ.
Net effective length for four sides = 4 × (a/2) = 2a
∴ Induced emf = Bvl = 2Bau
(b) Current in the frame is given by
(c) Total charge q, which flows through the sides of the frame, is given by
Here,
ΔΦ = Change in the flux
R = Resistance of the coil
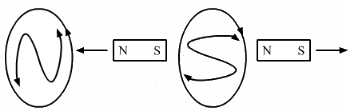
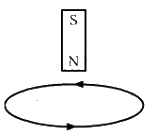
Q.14. The north pole of a magnet is brought down along the axis of a horizontal circular coil (see the following figure). As a result, the flux through the coil changes from 0.35 weber to 0.85 weber in an interval of half a second. Find the average emf induced during this period. Is the induced current clockwise or anticlockwise as you look into the coil from the side of the magnet?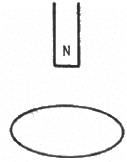
Given:-
Initial flux, ϕ1 = 0.35 weber
Final flux ϕ2 = 0.85 weber
∴ Δϕ = ϕ2 − ϕ1
= (0.85 − 0.35) weber
= 0.5 weber
Also,
Δt = 0.5 s
The magnitude of the induced emf is given by
The induced current is anti-clockwise when seen from the side of the magnet.
Q.15. A wire-loop confined in a plane is rotated in its own plane with some angular velocity. A uniform magnetic field exists in the region. Find the emf induced in the loop.
When the wire loop is rotated in its own plane in a uniform magnetic field, the magnetic flux through it remains the same. Because there is no change in the magnetic flux, the emf induced in the wire loop is zero.
Q.16. Figure shows a square loop of side 5 cm being moved towards right at a constant speed of 1 cm/s. The front edge enters the 20 cm wide magnetic field at t = 0. Find the emf induced in the loop at (a) t = 2 s, (b) t = 10 s, (c) t = 22 s and (d) t = 30 s.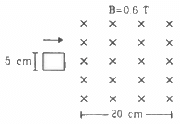
Given:-
Initial velocity, u = 1 cm/s
Magnetic field, B = 0.6 T
(a) At t = 2 s:-
Distance moved by the coil = 2 × 1 cm/s = 2 cm = 2 × 10-2m
Area under the magnetic field at t = 2s, A = 2 × 5 × 10-4m2
Initial magnetic flux = 0
Final magnetic flux = BA = 0.6 × (10 × 10-4)T-m2
Change in the magnetic flux, Δϕ = 0.6 × (10 × 10-4) - 0
Now, induced emf in the coil is
(b) At t = 10 s:-
Distance moved by the coil = 10 × 1 = 10 cm
At this time square loop is completely inside the magnetic field, so there is no change in the flux linked with the coil with time.
Therefore, induced emf in the coil at this time is zero.
(c) At t = 22 s:-
Distance moved = 22 × 1 = 22 cm
At this time loop is moving out of the field.
Initial magnetic flux = 0.6 × (5 × 5 × 10-4)T-m
At this time 2 cm part of the loop is ou t of the field.
Therefore, final magnetic flux = 0.6 × (3 × 5 × 10-4)T-m
Change in the magnetic flux, Δϕ = 0.6 × (3 × 5 × 10-4) - 0.6 × (5 × 5 × 10-4) = - 6 × 10-4)T-m2
Now, induced emf is
(d) At t = 30 s:-
At this time loop is completely out of the field, so there is no change in the flux linked with the coil with time.
Therefore, induced emf in the coil at this time is zero.
Q.17. Figure shows a square loop of side 5 cm being moved towards right at a constant speed of 1 cm/s. The front edge enters the 20 cm wide magnetic field at t = 0. Find the total heat produced in the loop during the interval 0 to 30 s if the resistance of the loop is 4.5 mΩ.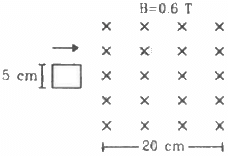
Resistance of the coil, R = 45 mΩ = 4.5 × 10−3 Ω
The heat produced is found by taking the sum of the individual heats produced.
Thus, the net heat produced is given by
H = H1 + H2 + H3 + H4
(a) Heat developed for the first 5 seconds:-
Emf induced, e = 3 × 10−4 V
Current in the coil,
H1 = (6.7 × 10−2)2 × 4.5 × 10−3 × 5
There is no change in the emf from 5 s to 20 s and from 25 s to 30 s.
Thus, the heat developed for the above mentioned intervals is given by
H2 = H4 = 0
Heat developed in interval t = 25 s to 30 s:-
The current and voltage induced in the coil will be the same as that for the first 5 seconds.
H3 = (6.7 × 10−2)2 × 4.5 × 10−3 × 5
Total heat produced:-
H = H1 + H3
= 2 × (6.7 × 10−2)2 × 4.5 × 10−2 × 5
= 2 × 10−4 J
Q.18. A uniform magnetic field B exists in a cylindrical region of radius 10 cm as shown in figure. A uniform wire of length 80 cm and resistance 4.0 Ω is bent into a square frame and is placed with one side along a diameter of the cylindrical region. If the magnetic field increases at a constant rate of 0.010 T/s, find the current induced in the frame.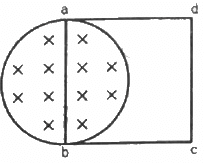
The magnetic field lines pass through coil abcd only in the part above the cylindrical region.
Radius of the cylindrical region, r = 10 cm
Resistance of the coil, R = 4 Ω
The rate of change of the magnetic field in the cylindrical region is constant and is given by
The change in the magnetic flux is given by
The induced emf is given by
The current in the coil is given by
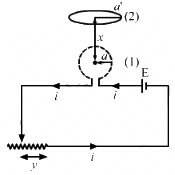
Q.19. The magnetic field in the cylindrical region shown in figure increases at a constant rate of 20.0 mT/s. Each side of the square loop abcd and defa has a length of 1.00 cm and a resistance of 4.00 Ω. Find the current (magnitude and sense) in the wire ad if (a) the switch S1 is closed but S2 is open, (b) S1 is open but S2 is closed, (c) both S1 and S2 are open and (d) both S1 and S2 are closed.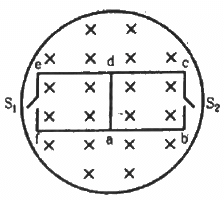
(a) When switch S1 is closed and switch S2 is open:-
Rate of change of the magnetic field = 20 mT/s = 2x10-4T/s
Net resistance of the coil adef, R = 4 × 4 = 16 Ω
Area of the coil adef = (10−2 )−2 = 10−4 m2
The emf induced is given by
= 10−4 × 2 × 10−2
= 2 × 10−6 V
The current through the wire ad is given by
= 1.25 × 10−7 A along ad
(b) When switch S2 is closed and switch S1 is open:-
Net resistance of the coil abcd, R = 16 Ω
The induced emf is given by
The current through wire ad is given by
(c) When both S1 and S2 are open, no current is passed, as the circuit is open. Thus, i = 0.
(d) When both S1 and S2 are closed, the circuit forms a balanced a Wheatstone bridge and no current flows along ad. Thus, i = 0.
Q.20. Figure shows a circular coil of N turns and radius a, connected to a battery of emf εthrough a rheostat. The rheostat has a total length L and resistance R. the resistance of the coil is r. A small circular loop of radius a' and resistance r' is placed coaxially with the coil. The centre of the loop is at a distance x from the centre of the coil. In the beginning, the sliding contact of the rheostat is at the left end and then onwards it is moved towards right at a constant speed v. Find the emf induced in the small circular loop at the instant (a) the contact begins to slide and (b) it has slid through half the length of the rheostat.
The magnetic field due to coil 1 at the centre of coil 2 is given by
The flux linked with coil 2 is given by
Now, let y be the distance of the sliding contact from its left end.
Given:-
v = dy/dt
Total resistance of the rheostat = R
When the distance of the sliding contact from the left end is y, the resistance of the rheostat (R') is given by R' = (R/L)y
The current in the coil is the function of distance y travelled by the sliding contact of the rheostat. It is given by
The magnitude of the emf induced can be calculated as:-
(a) For y = L,
(b) For y = L/2,
Q.21. A circular coil of radius 2.00 cm has 50 turns. A uniform magnetic field B = 0.200 T exists in the space in a direction parallel to the axis of the loop. The coil is now rotated about a diameter through an angle of 60.0°. The operation takes 0.100 s. (a) Find the average emf induced in the coil. (b) If the coil is a closed one (with the two ends joined together) and has a resistance of 4.00 Ω, calculate the net charge crossing a cross-section of the wire of the coil.
Given:-
Number of turns of the coil, N = 50
Magnetic field through the circular coil,
Radius of the circular coil, r = 2.00 cm = 0.02 m
Angle through which the coil is rotated, θ = 60°
Time taken to rotate the coil, t = 0.100 s
(a) The emf induced in the coil is given by
(b) The current in the coil is given by
The net charge passing through the cross section of the wire is given by
Q.22. A closed coil having 100 turns is rotated in a uniform magnetic field B = 4.0 × 10−4 T about a diameter which is perpendicular to the field. The angular velocity of rotation is 300 revolutions per minute. The area of the coil is 25 cm2 and its resistance is 4.0 Ω. Find (a) the average emf developed in half a turn from a position where the coil is perpendicular to the magnetic field, (b) the average emf in a full turn and (c) the net charge displaced in part (a).
Given:-
Number of turns in the coil, n = 100 turns
Magnetic field, B = 4 × 10−4
Area of the loop, A = 25 cm2 = 25 × 10−4 m2
(a) When the coil is perpendicular to the field:-
ϕ1 = nBA
When the coil goes through the half turn:-
ϕ2 = nBA cos 180° = −nBA
∴ Δϕ = 2nBA
When the coil undergoes 300 revolutions in 1 minute, the angle swept by the coil is
300 × 2π rad/min = 10π rad/s
10π rad is swept in 1 s.
π rad is swept in
(b) ϕ1 = nBA, ϕ2 = nBA (θ = 360°)
Δϕ = 0, thus emf induced will be zero.
(c) The current flowing in the coil is given by
= 0.5 × 10−3 = 5 × 10−4 A
Hence, the net charge is given by
Q = idt = 5 × 10−4 × (1/10)
= 5 × 10−5 C
Q.23. A coil of radius 10 cm and resistance 40 Ω has 1000 turns. It is placed with its plane vertical and its axis parallel to the magnetic meridian. The coil is connected to a galvanometer and is rotated about the vertical diameter through an angle of 180°. Find the charge which flows through the galvanometer if the horizontal component of the earth's magnetic field is BH = 3.0 × 10−5 T.
Given:-
Radius of the coil, r = 10 cm = 0.1 m
Resistance of the coil, R = 40 Ω
Number of turns in the coil, N = 1000
Angle of rotation, θ = 180°
Horizontal component of Earth's magnetic field, BH = 3 × 10−5 T
Magnetic flux, ϕ = NBA cos 180°
⇒ ϕ = −NBA
= −1000 × 3 × 10−5 × π × 1 × 1 × 10−2
= 3π × 10−4 Wb
dϕ = 2NBA = 6π × 10−4 Wb
Thus, the current flowing in the coil and the total charge are:-
Q.24. A circular coil of one turn of radius 5.0 cm is rotated about a diameter with a constant angular speed of 80 revolutions per minute. A uniform magnetic field B = 0.010 T exists in a direction perpendicular to the axis of rotation. Find (a) the maximum emf induced, (b) the average emf induced in the coil over a long period and (c) the average of the squares of emf induced over a long period.
Given,
Radius of the circular coil, R = 5.0 cm
Angular speed of circular coil, ω = 80 revolutions/minute
Magnetic field acting perpendicular to the axis of rotation, B = 0.010 T
The emf induced in the coil (e) is given by,
(a) For maximum emf, sinθ = 1
∴ e = BAω
⇒ e = 0.66 × 10−3 = 6.66 × 10−4 V
(b) The direction of the induced emf changes every instant. Thus, the average emf becomes zero.
(c) The emf induced in the coil is e = −BAωsinθ = −BAωsin ωt
The average of the squares of emf induced is given by
the rate of change of angle between the arc vector and B)
Q.25. A circular coil of one turn of radius 5.0 cm is rotated about a diameter with a constant angular speed of 80 revolutions per minute. A uniform magnetic field B = 0.010 T exists in a direction perpendicular to the axis of rotation. Suppose the ends of the coil are connected to a resistance of 100 Ω. Neglecting the resistance of the coil, find the heat produced in the circuit in one minute.
Given:-
T = 1 minute
Heat produced in the circuit is calculated using the following relation:-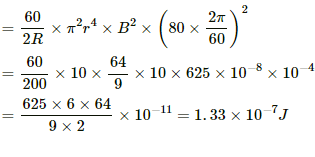
|
136 docs
|
FAQs on HC Verma Questions and Solutions: Chapter 38: Electromagnetic Induction- 2 - HC Verma Solutions - JEE
| 1. What is electromagnetic induction and how does it work? |  |
| 2. How is electromagnetic induction used in everyday life? | |
| 3. What are the factors that affect the magnitude of the induced voltage in electromagnetic induction? | |
| 4. Can electromagnetic induction be used to generate unlimited electrical energy? | |
| 5. How can electromagnetic induction be used to detect metal objects? | |
|
4.83/5 Rating |
|
Dec 23, 2024 Last updated |
|
Explore Courses for JEE exam
|
|
past year papers
,HC Verma Questions and Solutions: Chapter 38: Electromagnetic Induction- 2 | HC Verma Solutions - JEE
,Objective type Questions
,Extra Questions
,ppt
,practice quizzes
,mock tests for examination
,Sample Paper
,Previous Year Questions with Solutions
,shortcuts and tricks
,Summary
,Important questions
,Viva Questions
,HC Verma Questions and Solutions: Chapter 38: Electromagnetic Induction- 2 | HC Verma Solutions - JEE
,HC Verma Questions and Solutions: Chapter 38: Electromagnetic Induction- 2 | HC Verma Solutions - JEE
,MCQs
,Free
,Semester Notes
,video lectures
,Exam
,study material
;
HC Verma Questions and Solutions: Chapter 38: Electromagnetic Induction- 2 Free PDF Download
Importance of HC Verma Questions and Solutions: Chapter 38: Electromagnetic Induction- 2
HC Verma Questions and Solutions: Chapter 38: Electromagnetic Induction- 2 Notes
HC Verma Questions and Solutions: Chapter 38: Electromagnetic Induction- 2 JEE
Study HC Verma Questions and Solutions: Chapter 38: Electromagnetic Induction- 2 on the App
|
© EduRev
|
Education Revolution
|
|
