Class 8 Maths Chapter 5 HOTS Questions - Squares and Square Roots

Q1: How many numbers lie between squares of the following numbers?
(i) 12 and 13
(ii) 25 and 26
(iii) 99 and 100
Ans: As we know, between n² and (n+1)², the number of non–perfect square numbers are 2n.
(i) Between 12² and 13² there are 2 × 12 = 24 natural numbers.
(ii) Between 25² and 26² there are 2 × 25 = 50 natural numbers.
(iii) Between 99² and 100² there are 2 × 99 =198 natural numbers.

Q2: Write a Pythagorean triplet whose one member is:
(i) 6
(ii) 14
(iii) 16
(iv) 18
Ans: We know, for any natural number m, 2m, m²– 1, m² + 1 is a Pythagorean triplet.
(i) 2m = 6
⇒ m = 6/2 = 3
m²–1= 3² – 1 = 9–1 = 8
m²+1= 3²+1 = 9+1 = 10
Therefore, (6, 8, 10) is a Pythagorean triplet.
(ii) 2m = 14
⇒ m = 14/2 = 7
m²–1= 7²–1 = 49–1 = 48
m²+1 = 7²+1 = 49+1 = 50
Therefore, (14, 48, 50) is not a Pythagorean triplet.
(iii) 2m = 16
⇒ m = 16/2 = 8
m²–1 = 8²–1 = 64–1 = 63
m²+ 1 = 8²+1 = 64+1 = 65
Therefore, (16, 63, 65) is a Pythagorean triplet.
(iv) 2m = 18
⇒ m = 18/2 = 9
m²–1 = 9²–1 = 81–1 = 80
m²+1 = 9²+1 = 81+1 = 82
Therefore, (18, 80, 82) is a Pythagorean triplet.

Q3: (n+1)²-n² = ?
Ans: (n+1)²-n²
= (n² + 2n + 1) – n²
= 2n + 1

Q4: Show that 121 is the sum of 11 odd natural numbers.
Ans: As 121 = 11²
We know that the sum of first n odd natural numbers is n².
Therefore, 121 = sum of first 11 odd natural numbers
= 1 + 3 + 5+ 7 + 9 + 11 +13 + 15 + 17 + 19 + 21

Q5: Show that the sum of two consecutive natural numbers is 13².
Ans: Let 2n + 1 = 13
So, n = 6
So, ( 2n + 1)² = 4n² + 4n + 1
= (2n² + 2n) + (2n² + 2n + 1)
Substitute n = 6,
(13)² = ( 2 x 6² + 2 x 6) + (2 x 6² + 2 x 6 + 1)
= (72 + 12) + (72 + 12 + 1)
= 84 + 85

Q6: Use the identity and find the square of 189.
(a – b)² = a² – 2ab + b²
Ans: 189 = (200 – 11)²
= 40000 – 2 x 200 x 11 + 11²
= 40000 – 4400 + 121
= 35721

Q7: What would be the square root of 625 using the identity (a +b)² = a² + b² + 2ab?
Ans: (625)²
= (600 + 25)²
= 600² + 2 x 600 x 25 +25²
= 360000 + 30000 + 625
= 390625

Q8: Find the square roots of 100 and 169 by the method of repeated subtraction.
Ans: Let us find the square root of 100 first. 

• 100 – 1 = 99
• 99 – 3 = 96
• 96 – 5 = 91
• 91 – 7 = 84
• 84 – 9 = 75
• 75 – 11 = 64
• 64 – 13 = 51
• 51 – 15 = 36
• 36 – 17 = 19
• 19 – 19 = 0

Here, we have performed a subtraction ten times.
Therefore, √100 = 10
Now, the square root of 169:

• 169 – 1 = 168
• 168 – 3 = 165
• 165 – 5 = 160
• 160 – 7 = 153
• 153 – 9 = 144
• 144 – 11 = 133
• 133 – 13 = 120
• 120 – 15 = 105
• 105 – 17 = 88
• 88 – 19 = 69
• 69 – 21 = 48
• 48 – 23 = 25
• 25 – 25 = 0

Here, we have performed subtraction thirteen times.
Therefore, √169 = 13

Q9: Find the square root of 729 using factorisation method.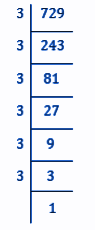

729 = 3×3×3×3×3×3×1
⇒ 729 = (3×3)×(3×3)×(3×3)
⇒ 729 = (3×3×3)×(3×3×3)
⇒ 729 = (3×3×3)²
Therefore,
⇒ √729 = 3×3×3 = 27

Q10: Find the smallest whole number by which 2800 should be divided so as to get a perfect square.
Ans: Let us first factorise the number 2800.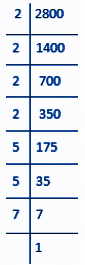

2800 = 2 × 2 × 2 × 2 × 5 × 5 × 7
= (2 × 2) × (2 × 2) × (5 × 5) ×7
Here, 7 cannot be paired.
Therefore, we will divide 2800 by 7 to get a perfect square.
New number = 2800 ÷ 7 = 400

Q11: 2025 plants are to be planted in a garden in such a way that each row contains as many plants as the number of rows. Find the number of rows and the number of plants in each row.
Ans: Let the number of rows be, x.
Therefore, the number of plants in each row = x.
Total many contributed by all the students = x × x = x²
Given, x² = Rs.2025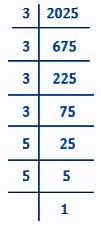

x² = 3 × 3 × 3 × 3 × 5 × 5
⇒ x² = (3 × 3) × (3 × 3) × (5 × 5)
⇒ x² = (3 × 3 × 5) × (3 × 3 × 5)
⇒ x² = 45 × 45
⇒ x = √(45 × 45)
⇒ x = 45
Therefore,
Number of rows = 45
Number of plants in each rows = 45

Q12: Find the smallest square number that is divisible by each of the numbers 8, 15 and 20.
Ans: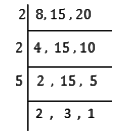 

L.C.M of 8, 15 and 20 is (2 × 2 × 5 × 2 × 3) = 120.
120 = 2 × 2 × 3 × 5 × 2 = (2 × 2) × 3 × 5 × 2
Here, 3, 5 and 2 cannot be paired.
Therefore, we need to multiply 120 by (3 × 5 × 2) i.e. 30 to get a perfect square.
Hence, the smallest squared number which is divisible by numbers 8, 15 and 20 = 120 × 30 = 3600