Squares and Square Roots Class 8 Worksheet Maths Chapter 5
| Table of contents |

|
| Multiple Choice Questions |

|
| Match the Column |

|
| Fill in the blanks |

|
| Find the square root using the method of prime factorization |

|
| Answer the following Questions |

|
Multiple Choice Questions
Q1: Which of the following is not a perfect square number?
A) 1156
B) 4657
C) 4624
D) 7056
Ans: B)
Sol: A perfect square is a number that can be expressed as the square of an integer.
Check if each option is a perfect square:
- is not a perfect square (not an integer square root).
Q2: A perfect square can never have the following digit in its ones place
A) 8
B) 4
C) 0
D) 1
Ans: A)
Sol: The last digit of a perfect square can be 0, 1, 4, 5, 6, or 9.
8 is not included in this list.
Q3: The sum of the first n odd natural numbers is
A) n2
B) 2n
C) n2+1
D) n2−1
Ans: A)
Sol: The sum of the first n odd natural numbers is known to be n2.
Q4: √0.09 is
A) 0.3
B) 0.03
C) 0.9
D) 0.33
Ans: A)
We need to find the square root of 0.09 by the long division method.
Q5: The area of the square field is 234.09 m2. The perimeter of the field id
A) 65.2 m
B) 59.6 m
C) 51.2 m
D) 61.2 m
Ans: D)
Sol:
- Area of the square =234.09m2
- Side length
- Perimeter
Q6: Given that √5625=75, the value of √0.5625 + √56.25 is:
A) 82.5
B) 0.75
C) 8.25
D) 75.05
Ans: C)
Sol:
√0.5625=0.75
√56.25=7.5
√0.5625+√56.25 = 0.75 + 7.5 = 8.25
Q7: Which of the following is a Pythagorean triplet?
A) 2,3,4
B) 6,8,10
C) 5,7,9
D) none of these
Ans: B)
Sol:
- A Pythagorean triplet (a,b,c) satisfies
- 102
Match the Column
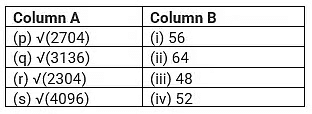
Ans:
(p) → (iv)
(q) → (i)
(r) → (iii)
(s) → (ii)
Fill in the blanks
Q1: There are _________ perfect squares between 1 and 100
Ans: 8
Sol:
- The perfect squares between 1 and 100 are
- There are 10 perfect squares between 1 and 100 inclusive. However, if considering only those strictly between 1 and 100, we exclude 1 and 100, giving us 8 perfect squares.
Q2: The square of a proper fraction is ______ than to the fraction
Ans: Smaller
Sol: A proper fraction is a fraction where the numerator is less than the denominator. When squared, the value is smaller.
Q3: The square of an even number is _____
Ans: even
Sol: The square of an even number is always even.
Q4: √4096 is ____
Ans: 64
Q5: The digit at the one's place of 372 is ____
Ans: 9
Sol: 372=1369, the digit at the one's place is 9.
Q6: The least number that must be added to 1500 to get a perfect square is ___
Ans: 39
The next perfect square after 1500 is 1539 (since 392).
Find the square root using the method of prime factorization
Q1: 121
Ans: 121 = 11 x 11
√121=11
Q2: 441
Ans: 441= 3 x 3 x 7 x 7
√441=3×7=21
Q3: 625
Ans: 625= 5 x 5 x 5 x 5
√625=5×5=25
Q4: 729
Ans: 729= 3 x 3 x 3 x 3 x 3 x 3
√729=3×3×3=27
Q5: 1521
Ans: 1521= 3 x 3 x 13 x 13
√1521=3×13=39
Answer the following Questions
Q1: Find the smallest number by which the following number must be multiplied to get a perfect square. Also, find the square root of the perfect square so obtained.
(i) 1008
(ii) 1280
(iii) 1875
Ans:
(i)1008= 2 x 2 x 2 x 2 x 3 x 3 x 7
We can see number 7 is not in a pair, so to make a perfect square, it has to be multiplied by 7
Then the number will become 7056
Now
7056= 2 x 2 x 2 x 2 x 3 x 3 x 7 x 7
√7056=2×2×3×7=84
(ii)1280=2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 5
We can see number 5 is not in a pair, so to make a perfect square, it has to be multiplied by 5
Then the number will become 6400
Now
6400= 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 5 x 5
√6400=2×2×2×2×5=80
(iii)1875= 3 x 5 x 5 x 5 x 5
We can see number 3 is not in a pair, so to make a perfect square, it has to be multiplied by 3
Then the number will become 5625
Now
5625= 3 x 3 x 5 x 5 x 5 x 5
√5625=3×5×5=75
Q2: 676 students are to be seated in a hall in such a way that each row contains as many students as the number of rows. Find the number of rows and the number of students in each row
Ans: Here, we need to find the square root of the Number 676
676=2 x 2 x 13 x 13
√676=2×13=26
So there are 26 rows, and each row has 26 students
Q3: What could be the possible ‘one’s’ digits of the square root of each of the following numbers?
(i) 1801
(ii) 856
(iii) 1008001
(iv) 6577525
Ans: (i) Last digit is 1, so one digit can be 1 or 9 as 12=1 and 92=81
(ii) Last digit is 6, so one digit can be 4 or 6 as 42=164 and 62=36
(iii) Last digit is 1, So one digit can be 1 or 9 as 12=1 =1 and 92=81
(iv) Last digit is 5, Ssoone digit will be 5 as 52=25
Q4: The students of a class arranged a gift for the class teacher. Each student contributed as many rupees as the number of students in the class. If the total contribution is Rs 1521, find the strength of the class.
Ans: Here, we need to find the square root of the Number 1521
1521= 3 x 3 x 13 x 13
√1521=3×13=39
So there are 39 students, and each contributed Rs 39
Q5: Find the least number that, when added to 4529 to make it a perfect square?
Ans: Let us find the square root of 4529 using the Long division method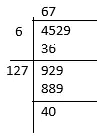
So the remainder is 40
Therefore, 672<4529
The next perfect square would be 682=4624
hence the number to be added = 4624 - 4529 = 95
So the addition of 95 to 4529 will make it a perfect square
Q6: Find the least number that must be subtracted from 2361 to make it a perfect square?
Ans: Let us find the square root of 2361 using the Long division method
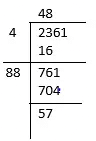
So the remainder is 57
Therefore, 482< 2361
Now, if we subtract the remainder from the main number, it will be a perfect square. So, subtraction of 57 from 2361 will make it a perfect square.
Q7: Find the smallest number by which the following number must be divided to get a perfect square. Also, find the square root of the perfect square so obtained.
(i)600
(ii)2904
Ans: (i) 600= 2 x 2 x 2 x 3 x 5 x 5
We can see numbers 2 and 3 are not in pairs, so to make a perfect square, it has to be divided by 6
Then the number will become 100
Now
100= 2 x 2 x 5 x 5
√100=2×5=10
(ii)2904=2 x 2 x 2 x 3 x 11 x 11
We can see numbers 2 and 3 are not in pairs, so to make a perfect square, it has to be divided by 6
Then the number will become 484.
Now
484= 2 x 2 x 11 x 11
√484=2×11=22
Q8: Find the value of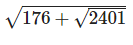
Ans: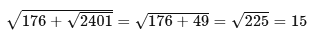
Q9: Find the square root of 83.3569
Ans: Square roots for decimals are found using the same long division method. We put bars on both the integral part and the decimal part. For integral, we move from the unit's place close to the decimal and move towards the left. For the decimal part, we start from the decimal and move towards the right
By the long division method

√83.3569=9.13
|
113 videos|630 docs|42 tests
|
FAQs on Squares and Square Roots Class 8 Worksheet Maths Chapter 5
| 1. What are squares and square roots? |  |
| 2. How can I find the square root using prime factorization? |  |
| 3. What is the importance of understanding squares and square roots in mathematics? |  |
| 4. Can every number have a square root? |  |
| 5. How do I solve problems involving squares and square roots in exams? |  |
















