Class 8 Exam > Class 8 Notes > Mathematics (Maths) Class 8 > Worksheet: Squares & Square Roots
Squares and Square Roots Class 8 Worksheet Maths Chapter 5
| Table of contents |
|
| Multiple Choice Questions |
|
| Match the Column |
|
| Fill in the blanks |
|
| Find the square root using the method of prime factorization |
|
| Answer the following Questions |
|
Multiple Choice Questions
Q1: Which of the following is not a perfect square number?
A) 1156
B) 4657
C)4624
D) 7056
Q2: A perfect square can never have the following digit in its ones place
A) 8
B) 4
C) 0
D) 1
Q3: The sum of first n odd natural numbers is
A) n2
B) 2n
C) n2+1
D) n2−1
Q4: √0.09 is
A) 0.3
B) 0.03
C) 0.94
D) 0.33
Q5: The area of the square field is 234.09 m2. The perimeter of the field id
A) 65.2 m
B) 59.6 m
C) 51.2 m
D) 61.2 m
Q6: Given that √5625=75, the value of √0.5625 + √56.25 is:
A) 82.5
B) 0.75
C) 8.25
D) 75.05
Q7: Which of the following is a pythogorean triplet?
A) 2,3,4
B) 6,8,10
C) 5,7,9
D) none of these
Match the Column
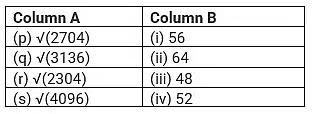
Fill in the blanks
Q1: There are _________ perfect squares between 1 and 100
Q2: The square of a proper fraction is ______ than to the fraction
Q3: The square of a even number is _____
Q4: √4096 is ____
Q5: The digit at the ones place of 372 is ____
Q6: The least number that must be added to 1500 so as to get a perfect square is ___
Find the square root using the method of prime factorization
Q1: 121
Q2: 441
Q3: 625
Q4: 729
Q5: 1521
Answer the following Questions
Q1: Find the smallest number by which following number must be multiplied to get a perfect square. Also, find the square root of the perfect square so obtained.
(i) 1008
(ii) 1280
(iii) 1875
Q2: 676 students are to be sit in a hall in such a way that each row contains as many students as the number of rows. Find the number of rows and the number of students in each row
Q3: What could be the possible ‘one’s’ digits of the square root of each of the following numbers?
(i) 1801
(ii) 856
(iii) 1008001
(iv) 6577525
Q4: The students of a class arranged a gift for the class teacher. Each student contributed as many rupees as the number of students in the class. If the total contribution is Rs 1521, find the strength of the class.
Q5: Find the least number which when added to 4529 to make it a perfect square?
Q6: Find the least number which must be subtracted from 2361 to make it a perfect square?
Q7: Find the smallest number by which following number must be divided to get a perfect square. Also, find the square root of the perfect square so obtained.
(i) 600
(ii) 2904
Q8: Find the value of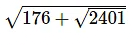
Q9: Find the square root of 83.3569
You can access the solutions to this worksheet here.
The document Squares and Square Roots Class 8 Worksheet Maths Chapter 5 is a part of the Class 8 Course Mathematics (Maths) Class 8.
All you need of Class 8 at this link: Class 8
|
79 videos|408 docs|31 tests
|
FAQs on Squares and Square Roots Class 8 Worksheet Maths Chapter 5
| 1. What is the method of prime factorization for finding square roots? |  |
Ans. The method of prime factorization involves breaking down a number into its prime factors. To find the square root, we group the prime factors into pairs. If there is an odd factor left, it cannot be paired, indicating that the number is not a perfect square. The square root is then the product of one factor from each pair.
| 2. How can I determine if a number is a perfect square? | |
Ans. A number is a perfect square if its prime factorization contains even exponents for all prime factors. For example, the number 36 can be factored into \(2^2 \times 3^2\), which indicates that it is a perfect square, as all the exponents (2 and 2) are even.
| 3. What are the first ten perfect squares? | |
Ans. The first ten perfect squares are:
1 (1x1),
4 (2x2),
9 (3x3),
16 (4x4),
25 (5x5),
36 (6x6),
49 (7x7),
64 (8x8),
81 (9x9),
100 (10x10).
| 4. How do you calculate the square root of a non-perfect square number? | |
Ans. To calculate the square root of a non-perfect square number, you can use the prime factorization method to get an approximate value. Alternatively, you can use a calculator or an estimation method, such as finding two consecutive perfect squares between which the number lies and using interpolation.
| 5. Why is understanding squares and square roots important in mathematics? | |
Ans. Understanding squares and square roots is fundamental in mathematics as it helps in various areas including algebra, geometry, and number theory. It is essential for solving quadratic equations, working with area calculations, and understanding the properties of numbers, which are foundational in advanced mathematics.
About this Document
|
4.70/5 Rating |
|
Dec 22, 2024 Last updated |
Document Description: Worksheet: Squares & Square Roots for Class 8 2024 is part of Mathematics (Maths) Class 8 preparation.
The notes and questions for Worksheet: Squares & Square Roots have been prepared according to the Class 8 exam syllabus. Information about Worksheet: Squares & Square Roots covers topics
like Multiple Choice Questions, Match the Column, Fill in the blanks, Find the square root using the method of prime factorization, Answer the following Questions and Worksheet: Squares & Square Roots Example, for Class 8 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Worksheet: Squares & Square Roots.
Introduction of Worksheet: Squares & Square Roots in English is available as part of our Mathematics (Maths) Class 8
for Class 8 & Worksheet: Squares & Square Roots in Hindi for Mathematics (Maths) Class 8 course.
Download more important topics related with notes, lectures and mock test series for Class 8
Exam by signing up for free. Class 8: Squares and Square Roots Class 8 Worksheet Maths Chapter 5
Description
Full syllabus notes, lecture & questions for Squares and Square Roots Class 8 Worksheet Maths Chapter 5 - Class 8 | Plus excerises question with solution to help you revise complete syllabus for Mathematics (Maths) Class 8 | Best notes, free PDF download
Information about Worksheet: Squares & Square Roots
In this doc you can find the meaning of Worksheet: Squares & Square Roots defined & explained in the simplest way possible. Besides explaining types of
Worksheet: Squares & Square Roots theory, EduRev gives you an ample number of questions to practice Worksheet: Squares & Square Roots tests, examples and also practice Class 8
tests
|
Explore Courses for Class 8 exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
study material
,Free
,Squares and Square Roots Class 8 Worksheet Maths Chapter 5
,shortcuts and tricks
,Viva Questions
,Previous Year Questions with Solutions
,Sample Paper
,Semester Notes
,Objective type Questions
,Extra Questions
,Exam
,MCQs
,mock tests for examination
,video lectures
,Important questions
,Summary
,past year papers
,Squares and Square Roots Class 8 Worksheet Maths Chapter 5
,practice quizzes
,ppt
,Squares and Square Roots Class 8 Worksheet Maths Chapter 5
;
Additional Information about Worksheet: Squares & Square Roots for Class 8 Preparation
Worksheet: Squares & Square Roots Free PDF Download
The Worksheet: Squares & Square Roots is an invaluable resource that delves deep into the core of the Class 8 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Worksheet: Squares & Square Roots now and kickstart your journey towards success in the Class 8 exam.
Importance of Worksheet: Squares & Square Roots
The importance of Worksheet: Squares & Square Roots cannot be overstated, especially for Class 8 aspirants.
This document holds the key to success in the Class 8 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Worksheet: Squares & Square Roots Notes
Worksheet: Squares & Square Roots Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Worksheet: Squares & Square Roots.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Worksheet: Squares & Square Roots Notes on EduRev are your ultimate resource for success.
Worksheet: Squares & Square Roots Class 8 Questions
The "Worksheet: Squares & Square Roots Class 8 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 8 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Worksheet: Squares & Square Roots on the App
Students of Class 8 can study Worksheet: Squares & Square Roots alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Worksheet: Squares & Square Roots,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Worksheet: Squares & Square Roots is prepared as per the latest Class 8 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup