Class 7 Maths Chapter 4 Practice Question Answers - Data Handling

Q1. Can the probability of an event be greater than 1? If yes enter 1 else 0.
(a) Can't determine
(b) 1
(c) 0
(d) none of these
Ans: (c)
Sol: No, the  probability of an event cannot be a negative number.
This is because of the Number of outcomes favorable to an event (E)≤  Number of all possible outcomes.
So, 0≤P(E)≤1

Q2. Value of the middle-most observation(s) is called:
(a) Mean
(b) Median
(c) Mode
(d) None of these
Ans: (b)
Sol: To find the Median, place the numbers in value order and find the middle number.
If there are two middle numbers, take the mean of the two numbers and this will be the median of the data set.
The middle most observation of a data series is called the median of the series.

Q3. Which one of the following cannot be the probability of an event?
(a) 0
(b) 1
(c) −1/6
(d) 2/3
Ans: (c)
Sol: Find the range of probability
Probability value lies between 0 and 1.
Where 0 is the probability of an impossible event while 1 is the probability of a sure event and 2/3 lies between 0 and 1.
But -1/6 < 0, so it can’t be the probability of any event.
Hence , the answer is option C as it is a negative number.

Q4. Median divides the total frequency into _____ equal parts.
(a) 2
(b) 3
(c) 4
(d) None of these
Ans: (a)
Sol: The median of the data series is the middle term or the mean of the two middle terms.
Hence, it divides the data series or the frequency of terms into two equal halves.

Q5. If P (E) denotes the probability of an event E, then
(a) P(E)<0
(b) P(E)>1
(c) 0≤P(E)≤1
(d) −1≤P(E)≤1
Ans: (c)
Sol: Probability is the measure of the likelihood that an event will occur.
Probability is referred as a number between 0 and 1.
0 indicates impossibility and 1 indicates certainty. The higher the probability of an event, the more likely it is that the event will occur.
so, the Probability of an even always lies between 0 and 1.
0≤P(E)≤1 is correct.

Q.6. When a die is thrown, list the outcomes of an event of getting a prime number.
(a) 2,3,5
(b) 1,3,5
(c) 3,5,7
(d) 1,2,5
Ans: (a)
Sol: For a dice, the possible outcomes are, 1, 2, 3, 4, 5, 6
To get a prime number, the possible outcomes are, 2, 3, 5

Q7. A child says that the median of 3,14,18,20,5 is 18. What concept does the child missed about finding the median?
(a) The order of numbers.
(b) 14
(c) 18
(d) None of these
Ans: (a)
Sol: To calculate the median of any data series. The data series has to be arranged in the ascending order. The child hasn't arranged the data series in ascending order.

Q8. Which of the following is not the outcome while Spinning a wheel.

(a) A
(b) B
(c) C
(d) E
Ans: (d)
Sol: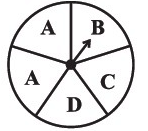

The outcome while Spinning a wheel is S=A,A,C,B,D
Since E is not in present in the wheel, hence it is not outcome

Q9. Mode of 2,3,4,5,0,1,3,3,4,3 is 3.
(a) True
(b) False
(c) Neither
(d) None
Ans: (a)
Sol: Mode is the term which appears maximum number of times.
The terms are: 2, 3, 4, 5, 0, 1, 3, 3, 4, 3
Arranging them in ascending order: 0, 1, 2, 3, 3, 3, 3, 4, 4, 5
3 is occurring maximum number of times. hence mode is 3.

Q10. The marks of 20 students in a test were as follows:
5,6,8,9,10,11,11,12,13,13,14,14,15,15,15,16,16,18,19,20.
The mean is
(a) 14
(b) 13
(c) 12
(d) 15
Ans: (b)
Sol: Marks are: 5,6,8,9,10,11,11,12,13,13,14,14,15,15,15,16,16,18,19,20.
Sum of marks =260
Number of students =20
Mean = Sum/Numbers = 260/20
= 13

Q11. A student got marks in 5 subjects in a monthly test is given below: 2,3,4,5,6.In these obtained marks, 4 is the
(a) Mean and median
(b) Median but no mean
(c) Mean but no median
(d) Mode
Ans: (a)
Sol: Marks obtained =2, 3, 4, 5, 6
Median is the middle term =4.
Mean = 2 + 3 + 4 + 5 + 6 / 5
= 4

Q12. The modal value is the value of the variate which divides the total frequency into two equal parts.
(a) True
(b) False
(c) Neither
(d) Either
Ans: (b)
Sol: False. Modal value is the value which occurs maximum number of times in the data.

Q13. State true or false:The mode is the most frequently occurring observation.
(a) True
(b) False
(c) Can't determine
(d) None of these
Ans: (a)
Sol: The observation occurring the most number of times or which has highest frequency is called the mode.
Thus, the given statement is true.

Q14. The marks of 20 students in a test were as follows:
5, 6, 8, 9, 10, 11, 11, 12, 13, 13, 14, 14, 15, 15, 15, 16, 16, 18, 19, 20
The mode is
(a) 20
(b) 10
(c) 15
(d) 25
Ans: (c)
Sol: Terms are: 5, 6, 8, 9, 10, 11, 11, 12, 13, 13, 14, 14, 15, 15, 15, 16, 16, 18, 19, 20.
15 occurs most number of times (3 times).
Hence, 15 is the mode of the marks.

Q15. If the probability of an event of a random experiment is P(E)=0, then the event is called an impossible event is
(a) True
(b) False
(c) Can't determine
(d) None of these
Ans: (a)
Sol: If P(E)=0, this event will never happen, hence it is an impossible event.

Q16. Median of 15, 28, 72, 56, 44, 32, 31, 43 and 51 is 43.
(a) True
(b) False
(c) Neither
(d) Either
Ans: (a)
Sol: The terms are: 15, 28, 72, 56, 44, 32, 31, 43 and 51.
Arranging them in ascending order: 15, 28, 31, 32, 43, 44, 51, 56, 72
Since the total number of terms is odd that is 9, therefore the median will be the middle term that is the 5th term which is 43.

Q17. Mean of 41,39,48,52,46,62,54,40,96,52,98,49,42,52,60 is 54.8
(a) True
(b) False
(c) Neither
(d) None
Ans: (b)
Sol: Mean = Sum of all numbers / No. of numbers
Mean =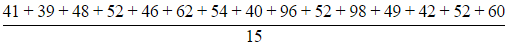
= 55.4

Q18. Calculate the mode for 17, 12, 19, 11, 20, 11, 20, 19, 10, 25, 19.
(a) 12
(b) 17
(c) 19
(d) 25
Ans: (c)
Sol: Mode is the value which occurs most often in the data set of values.
Given data set is 17,12,19,11,20,11,20,19,10,25,19
In the above data set, value  19 has occurred many times i.e., 3 times.
Therefore the mode of the given data set is 19

Q19. Find the arithmetic mean of integers from −5 to 5
(a) −1
(b) 0
(c) 1
(d) None of these
Ans: (b)
Sol: Integers from −5 to +5 are =−5,−4,−3,−2,−1, 0, 1, 2, 3, 4, 5
Sum of all these integers =0
So Mean =0

Q20. The mean of 8,7,9,10,12,x and 14 is 12, then find the value of x.
(a) 21
(b) 22
(c) 23
(d) 24
Ans: (d)
Sol: Given mean is 12.
Therefore, mean = 8 + 7+ 9 + 10 + 12 + x + 14 / 7
⇒ 12 = 60 + x / 7
⇒ 84 = 60 + x
⇒ x = 24

Q21. Find the mean of:
3,5,3,4,2,0,7 and 10

(a) 3.5
(b) 3.75
(c) 4
(d) 4.25
Ans: (d)
Sol: We need to find mean of 3,5,3,4,2,0,7 and 10.
Therefore, mean = 3 + 5 + 3 + 4 + 2 + 0 + 7 + 10 / 8
= 34/5
= 4.25

Q22. Find the mean of integers from −4 to 5
(a) −1
(b) 0
(c) 0.5
(d) 1
Ans: (c)
Sol: Integers from −4 to +5 are =−4,−3,−2,−1,0,1,2,3,4,5
Sum of all these integers =5
Total elements =10
So Mean = 5/10 = 0.5

Q23. Find the mean of: 5,15,20,8 and 12.
(a) 12
(b) 11
(c) 10
(d) 9
Ans: (a)
Sol: The observations are: 5,15,20,8,12
Mean = Sum / Number of Observations
Mean = 5 + 15 + 20 + 8 + 12 / 5
Mean = 60/5 = 12

Q24. Find the mean of 43, 51, 50, 57 and 54
(a) 50
(b) 51
(c) 55
(d) 57
Ans: (b)
Sol: The observations are : 43,51,50,57 and 54
Mean = Sum / Count of numbers
Mean = 43 + 51 + 50 + 57 + 54 / 5
Mean = 255 / 5
= 51

Q25. Mean of 130,126,68,50,1 is
(a) 80
(b) 82
(c) 157
(d) 75
Ans: (d)
Sol: Required mean = 30 + 126 + 68 + 50 + 1 / 5
= 375/5
= 75

Q26. The mean of first six natural numbers is
(a) 5
(b) 3.5
(c) 4
(d) None of these
Ans: (b)
Sol:
Step -1: Find the sum of first six natural numbers.
The first six natural numbers are 1, 2, 3, 4, 5, 6
Sum of these observations=1 + 2 + 3 + 4 + 5 + 6
= 21
Step -2: Find the mean of first six natural numbers.
Here, number of observations = 6
Mean =  Sum of observations / Number of observations
∴ Mean of first six natural numbers = 21/6
= 3.5

Q27. The difference between the greatest and the least value of the observations is known as
(a) M.D
(b) S.D
(c) Range
(d) Variance
Ans: (c)
Sol: The difference between the greatest and the least value of the observations is defined as Range.

Q28. The mean of 994, 996, 998, 1000 and 1002 is
(a) 992
(b) 1004
(c)  998
(d)  999
Ans: (c)
Sol: Given observations: 994, 996, 998, 1000, 1002
Mean = 994 + 996 + 998 + 1000 + 1002 / 5
Mean = 4990 / 5
Mean = 998

Q29. Median of the observations 5, 7, 14, 12, 15, 17, 17, 5, 14, 7, 5 is
(a) 14
(b) 12
(c) 11.8
(d) 7
Ans: (b)
Sol: By arranging the given no's in increasing order, we get:
 5,5,5,7,7,12,14,14,15,17,17
Total terms =11
Since, the middle most term is 6^th
∴ Value of median is 12

Q30. Find the mode of 14, 25, 14, 28, 18, 17, 18, 14, 23, 22, 14, 18.
(a) 14
(b) 25
(c) 28
(d) 18
Ans: (a)
Sol: Here, we arrange the data in the ascending order :- 14, 14, 14, 14, 17, 18, 18, 18, 22, 23, 25, 28
The value 14 has maximum frequency.
Therefore, the mode of the data is 14.