Class 8 Maths Chapter 12 HOTS Questions - Factorisation

Clear all your Class 8 doubts with EduRev Join for Free

Join for Free

Q1: Factorize:
6x² +11x−10
Ans: 6x²+11x−10
=6x²+15x−4x−10
=3x(2x+5)−2(2x+5)
=(3x−2)(2x+5)

Q2: Factorize:
3x²−14x+18
Ans: 3x² −14x+18
Factor with discriminant method,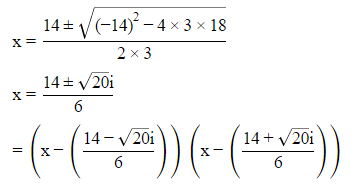

Q3: Factorize the following:(16−81x²)
Ans: Simplifying 16−81x²
16−81x 2
=(4)² −(9x)²
=(4+9x)(4−9x)

Q4: Factorise X² −7X + 10 = 0
Ans: Simplifying X² −7X+10=0
X² −5X−2X+10=0
X(X−5)−2(X−5)=0
(X−5)(X−2)=0

Q5: Divide (4x² −17xy+4y² )by(x−4y)
Ans: 4x²−17xy+4y²=4x²−16xy−xy+4y²
⇒4x(x−4y)−y(x−4y)
⇒(x−4y)(4x−y)
=(4x−y)

Q6: Factorise:15x+5
Ans: Simplifying 15x+5.
15x+5=5(3x+1)

Q7: Factorize: 2x² −7x−15
Ans: Simplifying the equation,
2x² −7x−15
=2x² −10x+3x−15
=2x(x−5)+3(x−5)
=(2x+3)(x−5)

Q8: Simplify: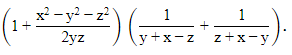

Ans: Now,

Q9: Factorize y² −(a+b)y+ab
Ans: Step 1: Open the bracket and simplify.
y² −(a+b)y+ab=y² −ay−by+ab
=y(y−a)−b(y−a)
=(y−a)(y−b)
Hence, (y-a) (y-b) are the two factors.

Q10: x³−2x²−x+2
Ans: x³−2x²−x+2
=x²(x−2)−1(x−2)
=(x²−1)(x−2)
=(x+1)(x−1)(x−2)

Q11: Factorize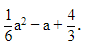
Ans: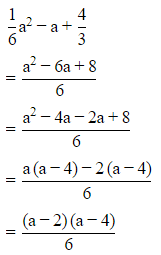

Hence, the answer is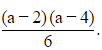

Q12: Find the factors of y² −7y+12.
Ans: y² −7y+12
y² −3y−4y+12
y(y−3)−y(y−3)
(y−3)(y−4)
∴ y=3,4

Q13: Factorise: 2p(x+y)−3q(x+y)
Ans: Since in the expression 2p(x+y)−3q(x+y), (x+y) is the common term, therefore, can be factorised as follows:
2p(x+y)−3q(x+y)=(x+y)(2p−3q)

Q14: Factorise: 3x² +6x+6
Ans: Since in the equation 3x² +6x+6, 3 is the common term, therefore, can be factorised as follows:
3x²+6x+6=3(x²+2x+2)

Q15: Factorise: 4abx² +8abx+12aby
Ans: Since in the equation 4abx² +8abx+12aby, 4ab is the common term, therefore, can be factorised as follows:
4abx² + 8abx+12aby=4ab(x² + 2x + 3y)

Q16: Factorise: 18x²y=24xyz
Ans: Since in the expression 18x²y−24xyz, 6xy is the common term, therefore, can be factorised as follows:
18x²y−24xyz=6xy(3x−4z)

Q17: Factorise: 5x² - 20xy
Ans: Since in the expression 5x² −20xy,  5x is the common term, therefore, can be factorized as follows:
5x²−20xy=5x(x−4y)

Q18: Factorize: 4(a+b)² −6(a+b)
Ans: Since in the expression 4(a+b)² −6(a+b), 2(a+b) is the common in both the terms,
therefore, the given expression can be factorised as follows:
4(a+b) 2−6(a+b)
=2(a+b)[2(a+b)−3]
=2(a+b)(2a+2b−3)

Q19: Factorise m² +m+1=0.
Ans: m 2 +m+1=0
factorise this quadratic equation by
Discriminant method.
D=1−4×1=−3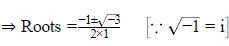


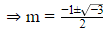
⇒m=−1± √3i
∴m= √3i−1or(− √3i−1)

Q20: Factories the given algebraic expression by taking out the common terms. Also, write the common term
5pq+20p³ q³ −15p² q
Ans: We first factorize each term of the given expression 5pq+20p³q³ −15p²q as shown below:
5pq=5×p×q
20p³ q³ =2 × 2 × 5 × p × p × p × q × q × q
15p²q = 3 × 5 × p × p × q
The common factors are 5,p and q, therefore, the HCF is 5×p×q=5pq.
Now, by taking out the common term(HCF), we have:
5pq+20p ³ q ³ −15p ² q=5pq(1+4p ² q ² −3p)
Hence, the common term is 5pq.