Worksheet Questions And Solutions : Comparing Quantities
Multiple Choice Questions
Q1: The ratio of 50cm to 2.5m is
(a) 10 : 1
(b) 5 : 1
(c) 1 : 5
(d) None of these
Ans: (c)
We know that 1m = 100cm
2.5m = 2.5 × 100 = 250cm
Ratio of 50cm to 2.5m =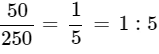 
Q2: The number of unelectrified villages in India decreased from 18,000 to 12,000 in the last 6 years. What is the percentage of decrease?
(a) 30%
(b) 50%
(c)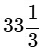 
(d) None of these.
Ans: (c)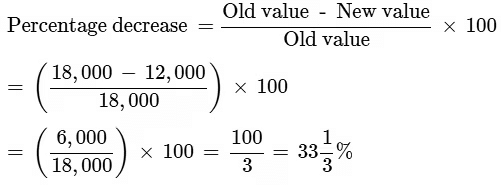
Q3: Cost of an item is Rs. 50. It was sold with a profit of 12%. Find the selling price
(a) Rs.56
(b) Rs. 60
(c) Rs.70
(d) None of these.
Ans: (a)
We know that
Cost Price = Rs. 50
and, Profit % = 12
Therefore, Profit =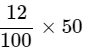 
⇒ Profit = 6⇒ S.P. = C.P. + Profit
⇒ S.P. = 50 + 6
⇒ S.P. = Rs 56
Q4: The simple interest on Rs.6000 for 1 year at 4% per annum is
(a) Rs.126.50
(b) Rs.240
(c) Rs.43
(d) None of these
Ans: (b)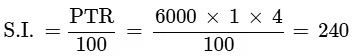
Q5: The fraction form of 45% is
(a) 3/20
(b) 9/20
(c) 11/20
(d) 13/2
Ans:(b)
45% = 45/100 = 9/20
True false
Q1. State whether the following statements are true or false :
(a) If the cost price of an item is more than the selling price, there is a profit.
Ans. False (If the cost price is more than the selling price, it results in a loss, not profit.)
(b) The formula for percentage is Percentage = ValueTotal/Value×100
Ans. False
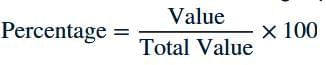
(c) Simple Interest is calculated using the formula SI = P×R×T/100, where P is the principal, R is the rate of interest, and T is the time in years.
Ans. True
(d) Discount is always calculated on the cost price of an item.
False (Discount is calculated on the marked price of an item.)
(e) The ratio of two quantities with the same units is expressed in the form of a fraction.
Ans. True
Answer the following Questions
Q1: Find the rate of discount given on a shirt whose selling price is ₹1092 after deducting a discount of ₹208 on its marked price.
Ans. We know that the SP = ₹1092
The discount = ₹208
By using the formula market price = SP + Discount
= 1092 + 208 = ₹1300
∴ The discount % = (discount/market price) × 100
= (208/1300) × 100 = 16%
Q2: In a constituency, there are 120 voters, 90 of them voted Yes. What per cent voted Yes?
Ans: Given:
Number of voters = 120
Number of voters who voted Yes = 90
Q3: A particular football team won 10 matches out of all the total number of matches they played. If their winning percentage was 40 %, how many matches did they play?
Ans:
Winning percentage
= Matches won/Total matches played × 100
Total matches played = 10 × 100 ÷ 40
Total matches = 25
Ans: The team played 25 matches.
Q4: My grandmother says in her childhood milk was at Rs.2 per litre. It was Rs.36 per litre today. By what percentage has the price gone up?
Ans: Given:
Old value = Rs. 2 per litre
New price = Rs. 36 per litre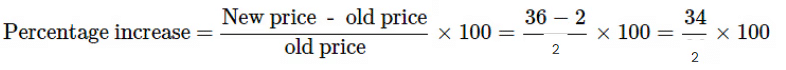
=1700%.
Q5: The cost of a toy car is Rs. 140. If the shopkeeper sells it at a loss of 10%. Find the price at which it is sold.
Ans: Given:
C.P. of toy car = Rs. 140
Loss% = 10%
S.P. =?
We know that,
Loss = C.P. - S.P.S.P. = C.P. - Loss
S.P. = 140 - 14
S.P. = Rs 126
Q6: Rashida purchased an air-conditioner for Rs. 3400, including a tax of 10%. Find the actual price of the air conditioner before VAT was added.
Ans: Let 'x' be the cost before adding VAT.
VAT = 10% of x = 0.1x
Cost after adding VAT = x + 0.1x = 1.1x
Given: cost = Rs.3,400
1.1x = Rs. 3400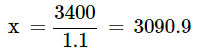
Thus, the price of an air-conditioner = Rs. 3090.9.
Q7: At what rate of simple interest will the sum double itself in 2 years?
Ans: We know that,
A = S.I. + P
Where,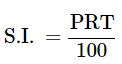
Given: A = 2 × principle = 2PTime = t = 2 years
R =?
Formula becomes 2P = S.I. + P
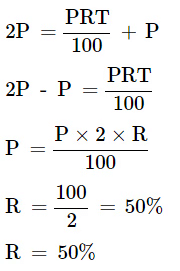Therefore, at the rate of 50%, the sum will double.
Q8: At what time will Rs. 1600 amount to Rs. 1768 at 6% per annum simple interest?
Ans: Given:
Principal = Rs. 1600
Amount = Rs. 1768
Rate = 6% per year
Time = ?
A = S.I. + P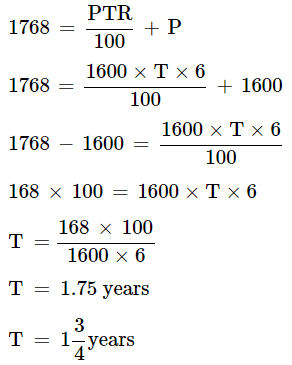
Q9: What amount does Harish have to pay at the end of 2 years of Rs. 40,000 at an interest of 16% compounded annually?
Ans: We know that, formula for compound interest,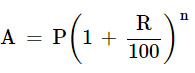
Where, P = principleN = no. of years
P = Rs. 40,000, R = 16%, n = 2.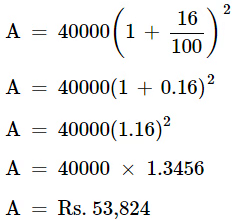
Amount paid by Harish at the end of 2 years is Rs. 53,824.
Q10:Compute the amount and compound interest on the principal amount ₹ 10,800 for 3 years at 12½ % per annum compounded annually.
Ans: Principal (P) = ₹ 10,800
Rate (R) = 12½ % = 25/2 % (annual)
Number of years (n) = 3
Amount (A) = P(1 + R/100)n
= 10800(1 + 25/200)3
= 10800(225/200)3
= 15377.34375
= ₹ 15377.34 (approximately)
Compound interest = A - P = ₹ (15377.34 - 10800) = ₹ 4,577.34
FAQs on Worksheet Questions And Solutions : Comparing Quantities
| 1. What is the difference between simple interest and compound interest in comparing quantities? |  |
| 2. How do you calculate percentage increase or decrease when comparing quantities? | |
| 3. What are some real-life applications of comparing quantities? | |
| 4. How can proportions be used when dealing with comparing quantities? | |
| 5. What are the common mistakes to avoid when comparing quantities? | |
