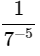Class 8 Maths - Exponents and Powers CBSE Worksheets
Multiple Choice Questions
Q1: What is the base of the exponent 69?
(a) 6
(b) 2
(c) 9
(d) None
Ans:(a)
The base of the exponent 69 is 6
Q2: Find the missing number 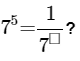 (a) 2
(a) 2
(b) −5
(c) 1
(d) None
Ans: (b)
The missing number should be −5
So the answer will be 75 =
Q3: Find the value of (52)2
(a) 125
(b) 625
(c) 25
(d) 0
Ans:(b)
The solution will be
(52)2=54
(52)2=5×5×5×5
(52)2= 625
Q4: Find the value of x, when 2x=44
(a) x=6
(b) x=2
(c) x=8
(d) x=−5
Ans: (c)
The solution will be
2x=44
2x=(22)4
2x=28
2x=28
x=8
So the answer will be x=8
Q5: Find the value of (211+62−51)0= ?
(a) 0
(b) −1
(c) 1
(d) None
Ans:(c)
The solution will be
(211+62−51)0=(anything)0
(211+62−51)0=1
So the solution will be
(211+62−51)0=1
State true or false
Q1: (100+120)(160+120)=82
Ans:False
(Anything)0 =1 therefore, LHS= 1
RHS= 82 = 64
hence false
Q2: (34)2=38
Ans:True
LHS= (34)2 = (3)8
RHS= (3)8
Q3: (52)3=100000
Ans:False
LHS= (52)3= (5)6 = 1000000 Hence false
Q4: Among 27,32,42, and 63, 63 is the greatest.
Ans: True
Sol: Since we have
27 = 2 × 2 × 2 × 2 × 2 × 2 × 2 = 128
32 = 3 × 3 = 9
42 = 4 × 4 = 16
63 = 6 × 6 × 6 = 216
In this, 63 is greater.
Q5: 625 can be expressed as 45.
Ans: False
Sol:
We have 625 = 5 × 5× 5 × 5 = 54.
Answer the following Questions
Q1: Follow the pattern and complete
Ans:The pattern for the solution is square root of the numbers which continue as
1234321=11112
123454321=111112
Q2: If 2x × 5x=1000 then x=?
Ans:For solving we will just factorise
2x ×5x=1000
2x × 5x = 5 × 5 × 5 × 2 × 2 × 2
2x × 5x = 23 × 53
x = 3
Q3: Find 33+ 43 + 53 and give the answers in cube
Ans: Solve the expression
33+43+53 = 27+64+125
33+43+53 = 216
33+43+53 = 6×6×6
33+43+53 = 63
Q4: Find the missing number x in 52+x2=132
Ans:Solve the expression
52+x2=132
25+x2=169
x2=144
x=√144
x=12
Q5: Simplify in exponent form (34× 32)÷ 3−4
Ans:Solving the expression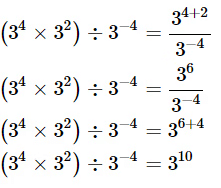 Q6: Expand
Q6: Expand
(a) 1526.26
(b) 8379
Using exponents
Ans:Solve in exponential form
(a) 1526.26 = 1×103+5×102+2×101+6×100 +2×10−1 + 6×10−2
(b) 8379 = 8×103+3×102+7×101+9×100
Q7: Express the following number as a product of powers of prime factors.
(a) 1225
(b) 3600
Ans:Solve in exponential form
(a) 1225=5×5×7×7
1225=52×72
(b) 3600=2×2×2×2×3×3×5×5
3600=24×32×52
Q8: Express the following large no’s in its scientific notation.
(a) 491200000
(b) 301000000
Ans:Solve in exponential form
(a) 491200000, move the decimal point 8 places to the left: 4.912×108
(b)9540000000000000, move the decimal point 15 places to the left: 9.54 × 1015
Q9: Express the following in usual form
(a) 3.02 ×10−6
(b) 5.8 × 1012
Ans: (a) 3.02 ×10−6
To convert a smaller number(negative powers of 10) to its usual form shift the decimal towards the left by the number of places equivalent to the power of 10.
3.02 × 10−6 = 3.02/1000000
∴ its usual form is 0.00000302
(b) 5.8 × 1012 = 5800000000000 [Moving the decimal towards the right by 12 places]
∴ its usual form is 5800000000000
Q10: Prove that  Ans:Solve the left hand side and equate with the right
Ans:Solve the left hand side and equate with the right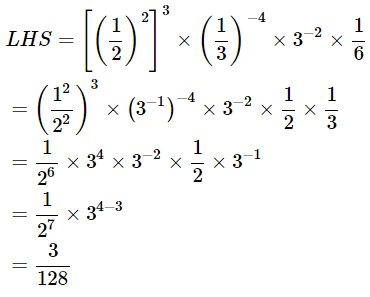
|
81 videos|452 docs|31 tests
|
FAQs on Class 8 Maths - Exponents and Powers CBSE Worksheets
| 1. What are exponents and how are they used in mathematical expressions? |  |
| 2. How do you multiply numbers with exponents? |  |
| 3. What is the difference between positive and negative exponents? |  |
| 4. How do you divide numbers with exponents? |  |
| 5. What are some real-life applications of exponents and powers? |  |