Class 7 Maths Chapter 1 Question Answers - Rational Numbers
Q1. Do −4 / 9 and −16 / 36 represent the same number?
Ans: −4 / 9 and −16 / 36
simplifying
−16 / 36

 Q2. List five rational numbers between −4 and −3.
Q2. List five rational numbers between −4 and −3.
Ans:
−4 x 6 / 6 = −24 / 6
−3 × 6 / 6 = −18 / 6
The rational numbers are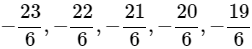
Q3. Give four equivalent numbers for 38.
Ans: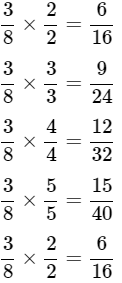
Q4. Rewrite the following rational numbers in the simplest form.
(a) 12 / 36
(b) 39 / 104
Ans:
(a) HCF of 12 and 36 is 12.
Dividing both numerator and denominator by 12,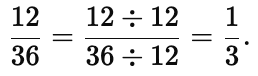
(b) HCF of 39 and 104 is 13.
Dividing both numerator and denominator by 13,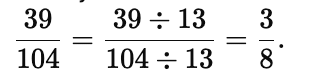 Q5. Find the value of
Q5. Find the value of 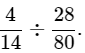
Ans:
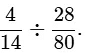

Q6. Find the product of 15/22 x 11/5
Ans: 15/22 x 11/5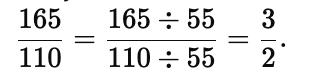 =
= 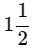
Q7. Find the value of 5/8 + 1/3
Ans: LCM of 8 and 3 is 24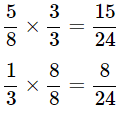
Therefore,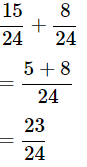
Q8. Find the value of
(a) 3/4 + 1/2
(b) 5/8 + 3/4
Ans:
(a) LCM of 4 and 2 is 4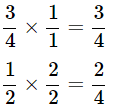
Therefore,
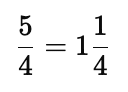
(b) LCM of 4 and 8 is 8
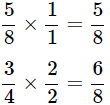
Therefore,
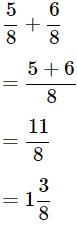
Q9. Simplify
(a) 2/5 - 1/2
(b) 1/5 - 3/4
Ans:
(a) LCM of 5 and 2 is 10
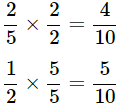
Therefore,
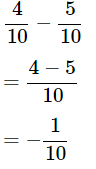
(b) LCM of 5 and 4 is 20
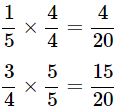
Therefore,
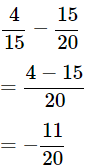
Q10. Find the product of
(a) 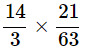
(b) 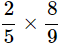
Ans:
(a)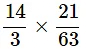
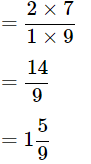
(b) 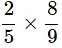
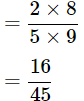
Q11. Insert six rational numbers between 3 / 8 and 3 / 5.
Ans: Convert both the denominators into the same denominator.
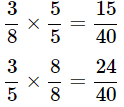
Therefore,
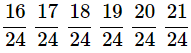
|
76 videos|452 docs|39 tests
|
FAQs on Class 7 Maths Chapter 1 Question Answers - Rational Numbers
| 1. What are rational numbers? |  |
| 2. How can I identify a rational number? |  |
| 3. Are all integers considered rational numbers? |  |
| 4. Can rational numbers be negative? |  |
| 5. What is the difference between rational and irrational numbers? |  |
















