Long Question Answer: Perimeter and Area | Mathematics (Maths) Class 7 PDF Download

Q1. State true or false.If the circumference of the circle is 88 cm, then its radius is 14 cm.
A. True
B. False
Ans:
Let radius be r
Circumference of the circle = 2 × π × r
⇒ 88 = 2 ×  22/7 × r
⇒ r = 14
Hence the radius is 14 cm

Q2. The circumference of a circular table is 88 m. Find the value of its area.
Ans:
As we know that circumference = 2π × r
⇒ 88 = 2 × π × r
⇒ r = 14
Now, area =  π × r2
⇒    = π×14²
⇒    = 616 m²

Q3. The radii of the inner and outer circumferences of a circular running track are 63 m and 70 m respectively. Find the area of track?
Ans:

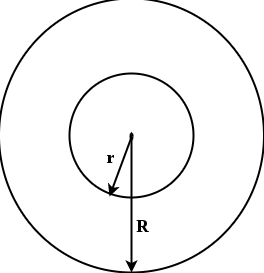Area of the region between two concentric circles with radius of outer circle R, and inner circler  
r = π(R² -r²)
Hence, the area of the circular track = π(70² - 63²) = 22/7 (4900 - 3969)
= 2926m²

Q4. Radii of two circles are 3 m and 4 m respectively. Find the radius of a circle having area equal to the sum of the areas of these two circles.
Ans:
We know the area of a circle =πr²
Hence, area of a circle(C₁ ) of radius 3 m= 22/7 ×(3)²
Area of a circle(C₂ ) of radius 4 m= 22/7 ×(4)²
Given, area of big circle = sum of the areas of circles C₁ and C₂
= 22/7 × 3² + 22/7 × 4²
= 22/7  × (9+16)
=  22/7  × (25)
Let the radius of the big circle be R.
Area of big circle =πR2 = 22/7 ×(25)
⇒ R2  = 25
⇒ R = 5  m

Q5. Can a paralleogram be contructed with AB = 4.5 cm, ∠B=120^∘  and the distance between AB and DC = 3.1 cm.
Ans:
Given: AB = 4.5cm, ∠B = 120^o and distance between AB and DC = 3.1cm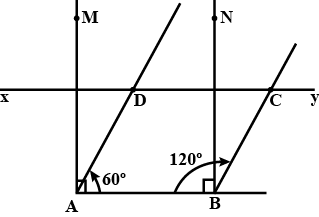Now, to construct a parallelogram with the above given values we will follow the below mentioned steps:1) Draw AB = 4.5cm
2) from point A, draw a line AM at angle 90^o
3) from point B, draw a line BN at angle 90^o
4) from point A and point B take an arc of length 3.1cm. Join point of intersecting of arc with line AM and BN, which gives line XY.
5) Where XY line is parallel to AB.
6) from point B draw a line at an angle of 120^o with the line AB and intersect with the line XY at point. Which give point C.
7) Since ABCD is parallelogram, sum of two adjacent angle is 180^o .
8) So, ∠A = 180^o − 120^o
⇒ ∠A = 60^o
9) from point A draw a line at an angle of 60^o with the line AB and intersecting with line XY at a point. Which give point D.
10) Now, ABCD is required parallelogram.
Hence, ABCD is a parallelogram.

Q6. Find the area of a flat circular ring formed by two concentric circles(circles with same centre) whose radii are 9 cm and 5 cm.
Ans:

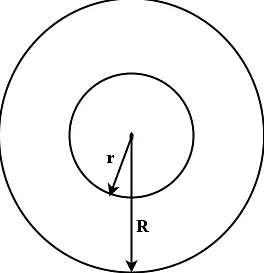
Area of the region between two concentric circles with radius of outer circle R, and inner circle
r =π(R² − r²)
Hence, the area of a flat circular ring formed by two concentric circles whose radii are 9 cm and 5 cm
= π(9² −5²)
= 22/7(81 − 25)
= 176cm2

Q7. There is a path of uniform width 7 m round and outside a circular garden of diameter 210 m. Find the area of the path.
Ans:
Radius of the circular garden, r = 210/2 =105m
Radius of the region covering the garden and the path, R = 105m + 7m  =  112m
Area of the region between two concentric circles with radius of outer circle R, and inner circle
r =π(R² −r²⁾
Hence, the area of the path = π(112² −105²)= 22/7 (12544 − 11025) =  33418/7
= 4774m²

Q8. A roller of diameter 0.9 m. and length 1.8 m is used to press the ground. Find the area of the ground pressed by it, in 500 revolutions.(Take π=3.14)
Ans:
Given,
Diameter of roller d=0.9 m
Length ℓ = 1.8 m
r =d/2
= 0.45
To find area it rolled in 1 revolution we have to find curved surface area.
Curved surface area:
= 2πrℓ
= 2 × 3.14 × 0.45 × 1.
= 5.0868 m²
Area covered in 500 revolutions
=500  x 5.0868
=2543.4 m²

Q9. Find the area of the triangle(in cm²) with base 6 cm and height 4 cm.
Ans:
Here, In △ABC, BC and AD are base and height of triangle.
∴  BC = 6cm and AD  = 4cm
⇒  Area of △ABC = 1/2 × BC × AD
= 1/2 x 6 x 4
= 12 cm²

Q10. The diameter of a wheel is 98 cm The number of revolutions it will have to make to cover a distance of 1540 m is?
Ans:
Given the diameter of wheel is 98 cm
Then radius of wheel = 98/2 = 49 cm
Then circumference of wheel = 2πr = 2× 22/7 × 49 = 308 cm

the number of revolutions to be made to cover a  distance of 1540 m = 1540 x 100 cm / 308 cm
= 154000 / 308
= 500

Q11. A flooring tile has the shape of a parallelogram whose base is 24 cm and the corresponding height is 10 cm. How many such tiles are required to cover a floor of area 1080 sq. metre.
Ans:
Area of one tile =24×10=240 cm²
It is known that 1 sq. meter =10000 cm²
Required no. of tiles = Total Area / Area of one tile = 1080 x 10000 / 240
= 45000 tiles

Q12. In given figure depicts a racing track whose left and right ends are semicircular. The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find:
(i) The distance around the track along its inner edge
(ii) The area of the track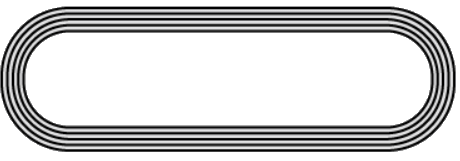

Ans:

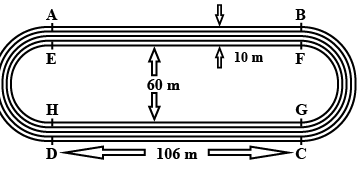The distance around the track along its inner edge = EF + HG + circumference of semicircle with diameter EH + circumference of semicircle with diameter FG circumference of semicircle with diameter EH + Circumference of semicircle with diameter FG=2 × π × 30
= 60πm
∴ The distance around the track along its inner edge
= 60π + 106 + 106
= 2804/7 m
∴  Area of track = Area of rectangle ABFE + Area of rectangle HGCD + (Area of semicircle with diameter AD − Area of semicircle with diameter EH) + (Area of semicircle with diameter BC − Area of semicircle with diameter FG)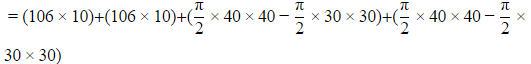

= 2120 + 2200
= 4320m²

Q13. The inner and outer diameter of the circular ring is 6 m and 12 m. Find its area.
Ans:
Area of a circular ring =  π / 4 (D²- d²)
= 3.14/4(12² - 6²)
= 84.78 cm²

Q14. The circumference of a circle is equal to 72 π. Find the radius of this circle.
Ans:
Given, Circumference of a circle = 72π
We know that Circumference = π d
dπ = 72π
d = 72
Since radius = d/2
∴ radius = 72/2 = 36

Q15. The area of a parallelogram is 153.6cm² . The base measures 19.2cm. What is the measurement for the height of the parallelogram?
Ans: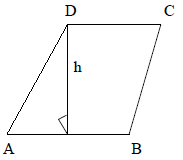

Area of the parallelogram is A = bh where b is the base and h is the height of the parallelogram.
It is given that area of the parallelogram is A = 153.6 cm²  and base b = 19.2cm, therefore,
153.6 = 19.2 × h
h = 153.6 / 19.2 = 8
Hence, the height of the parallelogram is 8 cm.