Polynomials Class 10 Worksheet Maths Chapter 2
Short Answer Type Questions
Q1: If a and b are roots of the equation x2 + 7 x + 7 . Find the value of a−1 + b−1 − 2αb ?
Ans: for f ( x ) = x2 + 7 x + 7
we get
α + b = − 7
αb = 7
Now a−1 + b−1 − 2αb
Q2: If the zeroes of the quadratic polynomial x2 + (α + 1 ) x + b are 2 and -3, then find the value of a and b.
Ans: Let f (x) = x2 + (a + 1) x + b
Then 2 − 3 = − ( a + 1 ) or α = 0
− 6 = b
So a = 0 and b = -6
Q.3. If a and b are zeroes of the polynomial f (x) = 2x2 − 7x + 3, find the value of α2 + b2.
Ans: f (x) = 2x2 − 7 x + 3
= 2x2 − x − 6 x + 3 = x(2x − 1) − 3(2 x − 1) = (x − 3) (2 x − 1)
So zeroes are 3 and 1/2
Now
α2 + b2
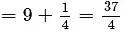
Q.4. Find the zeroes of the quadratic polynomial x2 + x − 12 and verify the relationship between the zeroes and the coefficients.
Ans: x2 + x − 12
= x2 + 4x − 3x − 12
= x (x + 4) − 3 (x + 4) = (x − 3) (x + 4)
So zeroes are 3 and -4
as we know
sum of roots = -b/a = -(1)/1 = -1 ie 3+(-4) = -1
product of roots = c/a = -12/1 = -12 ie 3x-4 = -12
Q5: If p and q are zeroes of f (x) = x2 − 5x + k, such that p − q = 1 , find the value of k.
Ans: for f ( x ) = x2 − 5 x + k
we get p + q = 5
pq = k
Now p − q = 1
(p − q)2 = 1
(p + q)2 − 4pq = 1
25 − 4k = 1
k = 6
Q6: Given that two of the zeroes of the cubic polynomial αx3 + bx2 + cx + d are 0, then find the third zero.
Ans: Two zeroes = 0, 0
Let the third zero be k.
The, using relation between zeroes and coefficient of polynomial, we have:
k + 0 + 0 = − b a
Third zero = k = -b/a
Q.7. If one of the zeroes of the cubic polynomial x3 + αx2 + bx + c is -1, then find the product of the other two zeroes.
Ans: 
Q8: If a-b, a , a+b , are zeroes of x3 − 6x2 + 8x , then find the value of b
Ans: Let f ( x ) = x3 − 6x2 + 8 x
Method -1
= x (x2 − 6 x + 8) = x(x − 2) (x − 4)
So 0,2,4 are zeroes of the polynomial. or a=2 and b=2 or -2 Method -2
Q9: Quadratic polynomial 4x2 + 12x + 9 has zeroes as p and q . Now form a quadratic polynomial whose zeroes are p − 1 and q − 1
Ans: 4x2 + 12 x + 9
= 4x2 + 6x + 6x + 9
= 2x(2x + 3) + 3(2x + 3) = (2 x + 3)2
So p = -3/2 and q = -3/2
So, p − 1 = − 5/2 and q − 1 = − 5/2
So quadratic polynomial will be
(x + 5/2)2
or
4x2 + 20 x + 25
Long Answer Type Questions
Q10: p and q are zeroes of the quadratic polynomial x2 − (k + 6 ) x + 2(2 k − 1) . Find the value of k if 2(p + q) = p q
Ans: for f (x) = x2 − (k + 6) x + 2 (2 k − 1)
We get, p + q = k + 6
p q = 2(2 k − 1)
Now 2 (p + q ) = pq
Therefore,
2 (k + 6) = 2(2k − 1)
or k + 6 = 2 k − 1
or k = 7
Q11: Given that the zeroes of the cubic polynomial x3 − 6 x2 + 3 x + 10 are of the form a, a + b, a + 2b for some real numbers a and b, find the values of a and b as well as the zeroes of the given polynomial.
Ans: k1 + k2 + k3 = 
a + a + b + a + 2b = 6
a + b = 2
a = 2 − b
Now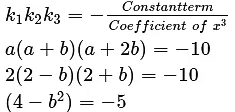
b=-3 or b=3
So a= 5 or -1
The zeroes with a = 5, b= -3 can be expressed as 5, 2, -1
The zeroes with a = -1, b = 3 can be expressed as -1, 2, 5
Q12: If one zero of the polynomial 2x2−5x−(2k + 1) is twice the other, find both the zeroes of the polynomial and the value of k.
Ans: Let a be one zero ,then another will be 2a
Now
α + 2α = 5/2 or a= 5/6
Also
k= -17/9
Q.13: Using division show that 3y2 + 5 is a factor of 6y5 + 15y4 + 16y3 + 4y2 + 10y − 35 .
Ans: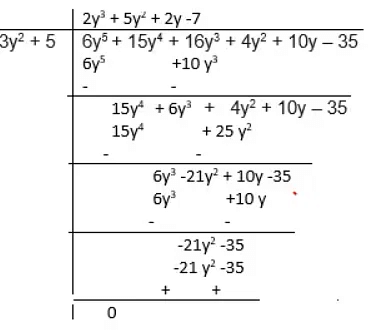
Q14: If (x - 2) and [x - 1/2 ] are the factors of the polynomials qx2 + 5x + r prove that q = r.
Ans: 4q + 10 + r = 0 -(1)
q/4 +5/2 + r = 0 or q + 10 + 4r = 0 -(2)
Subtracting 1 from 2
3q-3r = 0
q = r
Q15: Find k so that the polynomial x2 + 2x + k is a factor of polynomial 2x4 + x3 - 14x2 + 5x + 6. Also, find all the zeroes of the two polynomials.
Ans: For x2 + 2x + k is a factor of the polynomial 2x4 + x3 - 14x2 + 5x + 6, it should be able to divide the polynomial without any remainder
Comparing the coefficient of x, we get.
21 + 7k = 0
k = -3
So x2 + 2x + k becomes x2 + 2x -3 = (x-1)(x+3)
Now
2x4 + x3 - 14x2 + 5x + 6= (x2 + 2x -3)(2x2-3x-8+2k)
=(x2 + 2x - 3)(2x2-3x - 2)
=(x - 1)(x + 3)(x - 2)(2x + 1)
or x = 1, -3, 2,= -1/2
|
129 videos|736 docs|84 tests
|
FAQs on Polynomials Class 10 Worksheet Maths Chapter 2
| 1. What are polynomials and how are they classified? |  |
| 2. How do you add and subtract polynomials? |  |
| 3. What is the process for multiplying polynomials? |  |
| 4. How can polynomials be factored? |  |
| 5. What are the applications of polynomials in real life? |  |






















