Arithmetic Progression Class 10 Worksheet Maths

Multiple Choice Questions
Q1: For what value of a, are (2a - 1), 7 and 3a three consecutive terms of an A.P?
(a) 6
(b) 3
(c) 2
(d) 8
Ans: (b)
7 − (2a − 1 ) = 3a − 7
15 = 5 a
α = 3

Q2: Find the value of p, so that (3p + 7), (2p + 5), (2p + 7) are in A.P
(a) 5
(b) -5
(c) 4
(d) -4
Ans: (d)
(2p + 5)−(3p + 7) =(2p + 7)−(2p + 5)
−p − 2 = 2
p = −4

Q3: Solve the equation: 
1 + 4 + 7 + 10 + . . . + x = 287
(a) 40
(b) 41 
(c) 59 
(d) 54
Ans: (a)
Given, the sum of the terms up to x is 287.
We have to solve the equation.
The sum of the first n terms of an AP is given by
Sₙ = n/2[2a + (n-1)d]
Here, first term, a = 1
Common difference, d = 4 - 1 = 3
So, 287 = n/2[2(1) + (n - 1)3]
287 = n/2[2 + 3n - 3]
287 = n/2[3n - 1]
574 = n(3n - 1)
3n² - n = 574
3n² - n - 574 = 0
Using the quadratic formula,
n = -b±√(b²-4ac)/2a
Here, a = 3, b = -1 and c = -574
n = -(-1)±√((-1)²-4(3)(-574))/2(3)
= 1±√(1+6888)/6
= 1±√6889/6
n = (1±83)/6
Now, n = (1+83)/6 = 84/6 = 14
n = (1-83)/6 = -82/6 = -41/3
Since a negative term is not possible, n = -41/3 is neglected.
So, n = 14
The nth term of the series in AP is given by
aₙ = a + (n - 1)d
So, x = 1 + (14 - 1)(3)
= 1 + 13(3)
= 1 + 39
= 40
Therefore, the value of x is 40.

Q4: Find the sum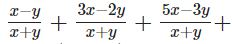
..upto 11 terms
(a)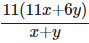
(b)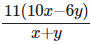
(c)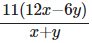
(d)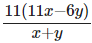

Ans: (d)


Q5: How many multiples of 4 lie between 10 and 250?
(a) 66
(b) 65
(c) 60
(d) 64
Ans: (c)
The AP will be 12, 16 ... 248
Now
248 = 12 + (n−1)4
n = 60

Short Answer Questions
Q6: Find the value of the middle most term (s) of the AP
-11, -7, -3,..., 49
Ans: Here a = - 11, d = 4
Now 49 = − 11 + (n − 1)4
n = 16
So middle most terms will 8 and 9
T₈ = − 11 + ( 8 − 1 ) 4 = 17
T₉ = − 11 + ( 9 − 1 ) 4 = 21

Q7: The 4th term of an A.P is equal to 3 times the first term and the 7th term exceeds twice the 3rd term by 1. Find the A.P
Ans: Let 1st term be a and common difference = d
According to the question,
T₄ = 3T₁ 
α + 3d = 3α
3d = 2a -(1)
Also, T₇ = 2T₃ + 1
α + 6d = 2 [a + (2 d] + 1
2d = a + 1 -(2)
Solving equation (1) and (2)
a = 3, d = 2
So, the AP formed is 3, 5, 7, 9, .........

Q8: The angles of a triangle are in A.P, the least being half the greatest. Find the angles
Ans: Let the angles be, (a-d), (a), (a+d)
Sum of the angles of a triangle is 180.
So, (a-d)+(a)+(a+d) = 180 ______(1)
3a = 180
a = 60
Also, from the given condition,
60-d = 1/2 (60+d)
2(60-d) = 60+d
120-2d = 60+d
120-60 = d+2d
60 = 3d
d = 20
Thus, the required angles are 40, 60, 80.

Long Answer Question
Q9: Find the sum of all three digit numbers which leave the remainder 3 when divided by 5.
Ans: The smallest 3 digit no. = 100 and greatest 3 digit number is 999
Since 100 is divisible by 5,adding 3 on 100 will provide the number which leave the remainder 3 when divided by 5
So the smallest three digit number which is divisible by 5 and gives reminder 3 = 103
The largest 3 digit no , 999/5 gives reminder 4 ,So subtracting 1 will the number which leave the remainder 3 when divided by 5
So the Largest three digit number which is divisible by 5 and gives reminder 3 = 998
Similarly we can find other numbers, the number will be given as
103, 108, 111,...998
Now  S = 103 + 108 + 111...+ 998
This is a AP with first term =103 and common difference = 5,last term = 998
Number of term can found from nth term formula
α_n = α₁ + (n−1) × d
998 = 103 + (n−1) × 5
n = 180
Therefore
S = 103 + 108 + 111...+ 998 =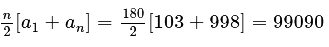


Q10: The sum of the 4th and 8th terms of an AP is 24 and the sum of the 6th and the 10th terms is 44. Find the first three terms of the AP
Ans: The formula for nth term of an AP is aₙ = a + (n - 1) d
Here, aₙ is the nth term, a is the first term, d is the common difference and n is the number of terms.
Given, a₄ + a₈ = 24
(a + 3d) + (a + 7d) = 24
⇒ 2a + 10d = 24
⇒ a + 5d = 12  ..... Equation(1)
Also, a₆ + a₁₀ = 44
(a + 5d ) + (a + 9d) = 44
⇒ 2a + 14d = 44
⇒ a + 7d = 22 .... Equation(2)
On subtracting equation (1) from (2), we obtain
(a + 7d ) - (a + 5d) = 22 - 12
a + 7d - a - 5d = 10
2d = 10
d = 5
By substituting the value of d = 5 in equation (1), we obtain
a + 5d = 12
a + 5 × 5 = 12
a + 25 = 12
a = - 13
The first three terms are a , (a + d) and (a + 2d)
Substituting the values of a and d , we get - 13, (- 13 + 5) and (- 13 + 2 × 5)
The first three terms of this A.P. are - 13, - 8, and - 3.