Class 7 Maths Chapter 6 Question Answers - The Triangle and Its Properties
Q1: In ∆ABC, write the following:
(a) Angle opposite to side BC.
(b) The side opposite to ∠ABC.
(c) Vertex opposite to side AC.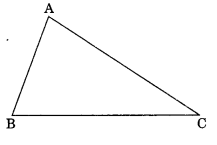 Sol:
Sol:
(a) In ∆ABC, Angle opposite to BC is ∠BAC
(b) Side opposite to ∠ABC is AC
(c) Vertex opposite to side AC is B
Q2: Which of the following cannot be the sides of a triangle?
(i) 4.5 cm, 3.5 cm, 6.4 cm
(ii) 2.5 cm, 3.5 cm, 6.0 cm
(iii) 2.5 cm, 4.2 cm, 8 cm
Sol:
(i) Given sides are, 4.5 cm, 3.5 cm, 6.4 cm
Sum of any two sides = 4.5 cm + 3.5 cm = 8 cm
Since 8 cm > 6.4 cm (Triangle inequality)
The given sides form a triangle.
(ii) Given sides are 2.5 cm, 3.5 cm, 6.0 cm
Sum of any two sides = 2.5 cm + 3.5 cm = 6.0 cm
Since 6.0 cm = 6.0 cm
The given sides do not form a triangle.
(iii) 2.5 cm, 4.2 cm, 8 cm
Sum of any two sides = 2.5 cm + 4.2 cm = 6.7 cm
Since 6.7 cm < 8 cm
The given sides do not form a triangle.
Q3: Classify the following triangle on the bases of sides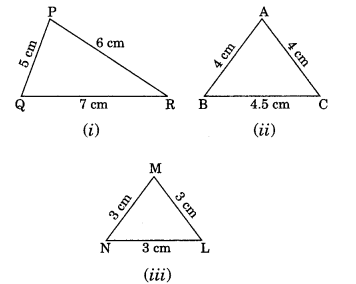 Sol:
Sol:
(i) PQ = 5 cm, PR = 6 cm and QR = 7 cm
PQ ≠ PR ≠ QR
Thus, ∆PQR is a scalene triangle.
(ii) AB = 4 cm, AC = 4 cm
AB = AC
Thus, ∆ABC is an isosceles triangle.
(iii) MN = 3 cm, ML = 3 cm and NL = 3 cm
MN = ML = NL
Thus, ∆MNL is an equilateral triangle.
Q4: In the given figure, find x.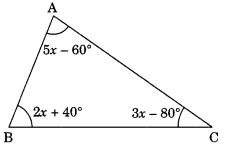
Sol:
In ∆ABC, we have
5x – 60° + 2x + 40° + 3x – 80° = 180° (Angle sum property of a triangle)
⇒ 5x + 2x + 3x – 60° + 40° – 80° = 180°
⇒ 10x – 100° = 180°
⇒ 10x = 180° + 100°
⇒ 10x = 280°
⇒ x = 28°
Thus, x = 28°
Q5: In the given figure, name the median and the altitude. Here E is the midpoint of BC.
Sol: In ∆ABC, we have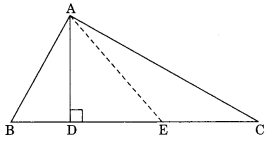 AD is the altitude.
AD is the altitude.
AE is the median.
Q6. One of the equal angles of an isosceles triangle is 50°. Find all the angles of this triangle.
Sol: Let the third angle be x°.
x + 50° + 50° = 180°
⇒ x° + 100° = 180°
⇒ x° = 180° – 100° = 80°
Thus ∠x = 80°
Q7. In the given diagrams, find the value of x in each case.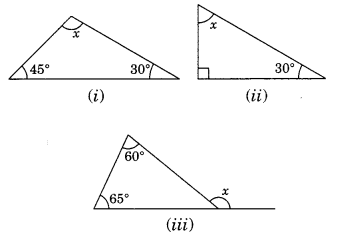 Sol:
Sol:
(i) x + 45° + 30° = 180° (Angle sum property of a triangle)
⇒ x + 75° – 180°
⇒ x = 180° – 75°
x = 105°
(ii) Here, the given triangle is right angled triangle.
x + 30° = 90°
⇒ x = 90° – 30° = 60°
(iii) x = 60° + 65° (Exterior angle of a triangle is equal to the sum of interior opposite angles)
⇒ x = 125°
Q8. In ΔABC, AC = BC and ∠C = 110°. Find ∠A and ∠B.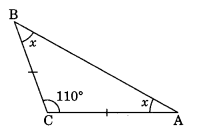 Sol:
Sol:
In given ΔABC, ∠C = 110°
Let ∠A = ∠B = x° (Angle opposite to equal sides of a triangle are equal)
x + x + 110° = 180°
⇒ 2x + 110° = 180°
⇒ 2x = 180° – 110°
⇒ 2x = 70°
⇒ x = 35°
Thus, ∠A = ∠B = 35°
|
77 videos|386 docs|39 tests
|





















