Areas Related to Circles Class 10 Worksheet Maths
Multiple Choice Questions
Q1: The part of the circular region enclosed by a chord and the corresponding arc of a circle is called(a) a segment
(b) a diameter
(c) a radius
(d) a sector
Ans: (a)The part of the circular region enclosed by a chord and the corresponding arc of a circle is called a segment.
Q2: If ‘r’ is the radius of a circle, then it's circumference is given by
(a) 2πr
(b) None of these
(c) πr
(d) 2πd
Ans: (a)
Sol: If the radius of a circle is given, the circumference or perimeter can be calculated using the formula below:-
Circumference = 2πr
Q3: The angle described by the minute hand between 4.00 pm and 4.25 pm is
(a) 900
(b) 1500
(c) 1250
(d) 1000
Ans: (b)
Sol:
Time duration between 4.00 pm and 4.25 pm = 25 minutes
Angle described by minute hand in 60 minutes = 3600
Angle described by minute hand in 25 minutes = 3600/600 × 25 = 1500
Q4: If a line meets the circle in two distinct points, it is called(a) a chord
(b) a radius
(c) secant
(d) a tangent
Ans: (c)
Sol: A secant line, also simply called a secant, is a line meet two points in a circle.
Q5: The perimeter of a protractor is
(a) πr
(b) πr+2r
(c) π+r
(d) π+2r
Ans: (b)
Sol: Let radius of the protractor be r ∴Perimeter of protractor = Perimeter of semicircle + Diameter of semicircle
⇒ Perimeter of protractor = πr + 2r
Q6: The perimeter of a circle having radius 5cm is equal to:
(a) 30 cm
(b) 3.14 cm
(c) 31.4 cm
(d) 40 cm
Ans: (c)
Sol: The perimeter of the circle is equal to the circumference of the circle.
Circumference = 2πr
= 2 x 3.14 x 5
= 31.4 cm
Q7: Area of the circle with radius 5cm is equal to:
(a) 60 sq.cm
(b) 75.5 sq.cm
(c) 78.5 sq.cm
(d) 10.5 sq.cm
Ans: (c)
Sol: Radius = 5cm
Area = πr2 = 3.14 x 5 x 5 = 78.5 sq.cm
Q8: The largest triangle inscribed in a semi-circle of radius r, then the area of that triangle is;
(a) r2
(b) 1/2r2
(c) 2r2
(d) √2r2
Ans: (a) r2
Sol: The height of the largest triangle inscribed will be equal to the radius of the semi-circle and base will be equal to the diameter of the semi-circle.
Area of triangle = ½ x base x height
= ½ x 2r x r
= r2
Q9: If the perimeter of the circle and square are equal, then the ratio of their areas will be equal to:
(a) 14:11
(b) 22:7
(c) 7:22
(d) 11:14
Ans: (a)
Sol: Given,
The perimeter of circle = perimeter of the square
2πr = 4a
a=πr/2
Area of square = a2 = (πr/2)2
Acircle/Asquare = πr2/(πr/2)2
= 14/11
Q10: The area of the circle that can be inscribed in a square of side 8 cm is
(a) 36 π cm2
(b) 16 π cm2
(c) 12 π cm2
(d) 9 π cm2
Ans: (b) 16 π cm2
Sol: Given,
Side of square = 8 cm
Diameter of a circle = side of square = 8 cm
Therefore, Radius of circle = 4 cm
Area of circle
= π(4)2
= π (4)2
= 16π cm2
Very Short Answer Question
Q1: A bicycle wheel makes 5000 revolutions in moving 11km.Find the diameter of the wheel.
Ans: 70 cm
Q2: A chord AB of a circle of radius 10 cm makes a right angle at the centre of the circle. Find the area of the minor and major segments.
Ans: 28.5cm2, 285.5cm2
Q3: Find the difference of the areas of a sector of angle 1200 and its corresponding major sector of a circle of radius 21 cm.
Ans: 462cm2
Q4: A boy is cycling such that the wheels of the cycle are making 140 revolutions per minute. If the diameter of the wheel is 60cm, calculate the speed per hour with which the boy is cycling.
Ans: 15.84 km/hr
Long Question Answer
Ans: Let the radius of each circular plate be r cm. Then,
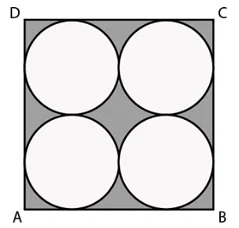 Length of each side of the square sheet = 4r cm.
Length of each side of the square sheet = 4r cm.
∴ Area of the square cardboard sheet = (4r 4r) cm2 = 16 r2 cm2
But, the area of the cardboard sheet is given to be 784 cm2
16r2 = 784 r2 = 49
r = 7
Area of one circular plate = = 154 cm
Area of four circular plates = 4× 154 cm2 = 616 cm2
Uncovered area of the square sheet = (784 - 616) cm2 = 168 cm2.
|
127 videos|584 docs|79 tests
|
FAQs on Areas Related to Circles Class 10 Worksheet Maths
| 1. What is the formula to find the area of a circle? |  |
| 2. How do you find the circumference of a circle? |  |
| 3. Can you find the area of a circle if only the diameter is given? |  |
| 4. How do you find the area of a sector of a circle? |  |
| 5. Can you find the area of a circle if only the circumference is given? |  |
















