Class 8 Exam > Class 8 Notes > Know Your Aptitude Class 6 To 8 > Worksheet: Rotation of Objects - 2
Worksheet: Rotation of Objects - 2 | Know Your Aptitude Class 6 To 8 - Class 8 PDF Download
Rotate the Point
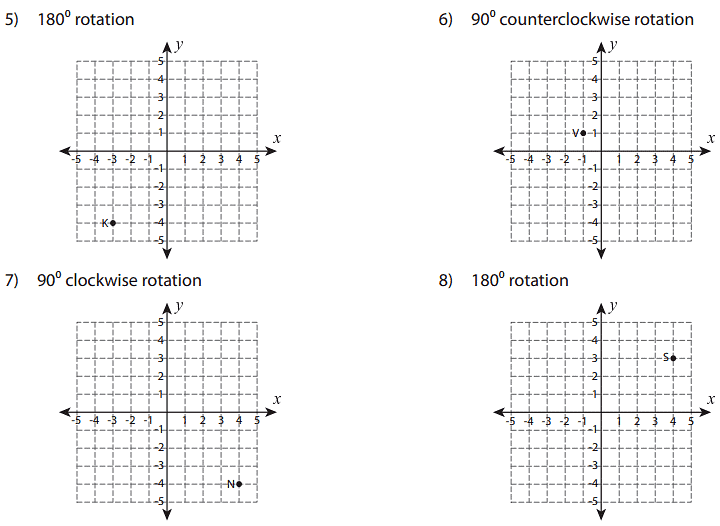
Q: Graph the new position of each point after rotating it about the origin.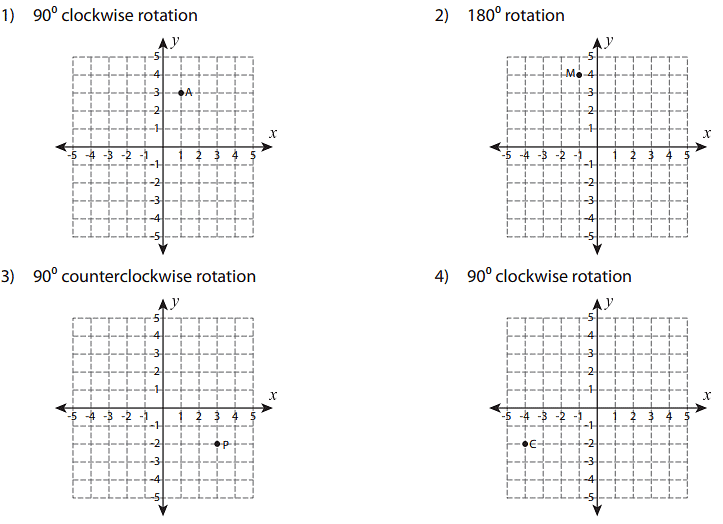
You can access the solutions to this worksheet here.
The document Worksheet: Rotation of Objects - 2 | Know Your Aptitude Class 6 To 8 - Class 8 is a part of the Class 8 Course Know Your Aptitude Class 6 To 8.
All you need of Class 8 at this link: Class 8
|
5 videos|60 docs|13 tests
|
FAQs on Worksheet: Rotation of Objects - 2 - Know Your Aptitude Class 6 To 8 - Class 8
| 1. What is the concept of rotating a point in a coordinate system? |  |
Ans.Rotating a point in a coordinate system involves changing its position based on a specified angle around a fixed point, usually the origin. This is often calculated using trigonometric functions, where the new coordinates (x', y') can be found using the rotation formulas: x' = x * cos(θ) - y * sin(θ) and y' = x * sin(θ) + y * cos(θ), where θ is the angle of rotation.
| 2. How do you rotate a point 90 degrees counterclockwise? | |
Ans.To rotate a point 90 degrees counterclockwise, you can use the rotation formulas. For a point (x, y), the new coordinates will be (-y, x). This means that if you have a point at (3, 2), after a 90-degree counterclockwise rotation, the new coordinates will be (-2, 3).
| 3. What are the steps to rotate multiple points around a center point? | |
Ans.To rotate multiple points around a center point, follow these steps:
1. Translate each point so that the center point is at the origin by subtracting the center point's coordinates from each point.
2. Apply the rotation formulas to each translated point.
3. Translate the points back by adding the center point's coordinates to the rotated points.
| 4. Can you explain the difference between clockwise and counterclockwise rotations? | |
Ans.Clockwise rotation moves points in the same direction as the hands of a clock, while counterclockwise rotation moves points in the opposite direction. When using rotation angles, positive angles typically represent counterclockwise rotations, whereas negative angles indicate clockwise rotations.
| 5. What applications do point rotations have in real life? | |
Ans.Point rotations have various applications in real life, including computer graphics for rendering images, robotics for path planning, and in navigation systems for determining directions. They are also essential in architecture and engineering for designing and visualizing structures.
About this Document
Oct 12, 2025
Last updated
Document Description: Worksheet: Rotation of Objects - 2 for Class 8 2025 is part of Know Your Aptitude Class 6 To 8 preparation.
The notes and questions for Worksheet: Rotation of Objects - 2 have been prepared according to the Class 8 exam syllabus. Information about Worksheet: Rotation of Objects - 2 covers topics
like Rotate the Point and Worksheet: Rotation of Objects - 2 Example, for Class 8 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Worksheet: Rotation of Objects - 2.
Introduction of Worksheet: Rotation of Objects - 2 in English is available as part of our Know Your Aptitude Class 6 To 8
for Class 8 & Worksheet: Rotation of Objects - 2 in Hindi for Know Your Aptitude Class 6 To 8 course.
Download more important topics related with notes, lectures and mock test series for Class 8
Exam by signing up for free. Class 8: Worksheet: Rotation of Objects - 2 | Know Your Aptitude Class 6 To 8 - Class 8
Description
Full syllabus notes, lecture & questions for Worksheet: Rotation of Objects - 2 | Know Your Aptitude Class 6 To 8 - Class 8 - Class 8 | Plus excerises question with solution to help you revise complete syllabus for Know Your Aptitude Class 6 To 8 | Best notes, free PDF download
Information about Worksheet: Rotation of Objects - 2
In this doc you can find the meaning of Worksheet: Rotation of Objects - 2 defined & explained in the simplest way possible. Besides explaining types of
Worksheet: Rotation of Objects - 2 theory, EduRev gives you an ample number of questions to practice Worksheet: Rotation of Objects - 2 tests, examples and also practice Class 8
tests
Related Searches
shortcuts and tricks
,Objective type Questions
,Important questions
,past year papers
,ppt
,practice quizzes
,Semester Notes
,Summary
,Free
,Exam
,MCQs
,Previous Year Questions with Solutions
,Sample Paper
,Worksheet: Rotation of Objects - 2 | Know Your Aptitude Class 6 To 8 - Class 8
,study material
,Viva Questions
,mock tests for examination
,Worksheet: Rotation of Objects - 2 | Know Your Aptitude Class 6 To 8 - Class 8
,Extra Questions
,video lectures
,Worksheet: Rotation of Objects - 2 | Know Your Aptitude Class 6 To 8 - Class 8
;
Additional Information about Worksheet: Rotation of Objects - 2 for Class 8 Preparation
Worksheet: Rotation of Objects - 2 Free PDF Download
The Worksheet: Rotation of Objects - 2 is an invaluable resource that delves deep into the core of the Class 8 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Worksheet: Rotation of Objects - 2 now and kickstart your journey towards success in the Class 8 exam.
Importance of Worksheet: Rotation of Objects - 2
The importance of Worksheet: Rotation of Objects - 2 cannot be overstated, especially for Class 8 aspirants.
This document holds the key to success in the Class 8 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Worksheet: Rotation of Objects - 2 Notes
Worksheet: Rotation of Objects - 2 Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Worksheet: Rotation of Objects - 2.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Worksheet: Rotation of Objects - 2 Notes on EduRev are your ultimate resource for success.
Worksheet: Rotation of Objects - 2 Class 8 Questions
The "Worksheet: Rotation of Objects - 2 Class 8 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 8 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Worksheet: Rotation of Objects - 2 on the App
Students of Class 8 can study Worksheet: Rotation of Objects - 2 alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Worksheet: Rotation of Objects - 2,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Worksheet: Rotation of Objects - 2 is prepared as per the latest Class 8 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup