Practice Questions: Triangles

Q1. In the given figure, PS/SQ = PT/TR and ∠ PST = ∠ PRQ. Prove that PQR is an isosceles triangle.

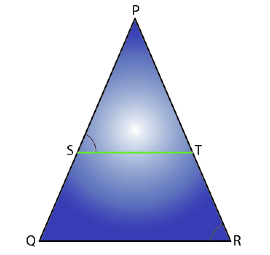
Sol:  Given,

PS/SQ = PT/TR

We know that if a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.

Therefore, ST ∥ QR

And ∠ PST = ∠ PQR (Corresponding angles) ........(i)

Also, given,

∠ PST = ∠ PRQ.........(ii)

From (i) and (ii),

∠ PRQ = ∠ PQR

Therefore, PQ = PR (sides opposite the equal angles)

Hence, PQR is an isosceles triangle.

Q2. In the figure, DE // AC and DF // AE. Prove that BF/FE = BE/EC.

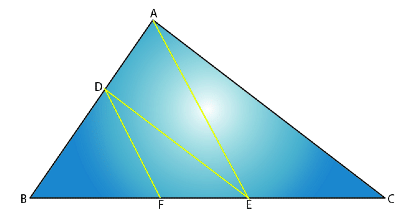
Sol: Given that,

In triangle ABC, DE // AC.

By Basic Proportionality Theorem,

BD/DA = BE/EC..........(i)

Also, given that DF // AE.

Again by Basic Proportionality Theorem,

BD/DA = BF/FE..........(ii)

From (i) and (ii),

BE/EC = BF/FE

Hence proved.

Q3. In the given figure, altitudes AD and CE of ∆ ABC intersect each other at the point P. Show that:
(i) ∆AEP ~ ∆ CDP
(ii) ∆ABD ~ ∆ CBE
(iii) ∆AEP ~ ∆ADB
(iv) ∆ PDC ~ ∆ BEC

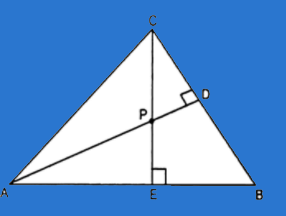
Sol: Given that AD and CE are the altitudes of triangle ABC and these altitudes intersect each other at P.

(i) In ΔAEP and ΔCDP,

∠AEP = ∠CDP (90° each)

∠APE = ∠CPD (Vertically opposite angles)

Hence, by AA similarity criterion,

ΔAEP ~ ΔCDP

(ii) In ΔABD and ΔCBE,

∠ADB = ∠CEB ( 90° each)

∠ABD = ∠CBE (Common Angles)

Hence, by AA similarity criterion,

ΔABD ~ ΔCBE

(iii) In ΔAEP and ΔADB,

∠AEP = ∠ADB (90° each)

∠PAE = ∠DAB (Common Angles)

Hence, by AA similarity criterion,

ΔAEP ~ ΔADB

(iv) In ΔPDC and ΔBEC,

∠PDC = ∠BEC (90° each)

∠PCD = ∠BCE (Common angles)

Hence, by AA similarity criterion,

ΔPDC ~ ΔBEC

Q4. A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower

Sol: Given,

Length of the vertical pole = 6 m

Shadow of the pole = 4 m

Let the height of the tower be h m.

Length of the shadow of the tower = 28 m

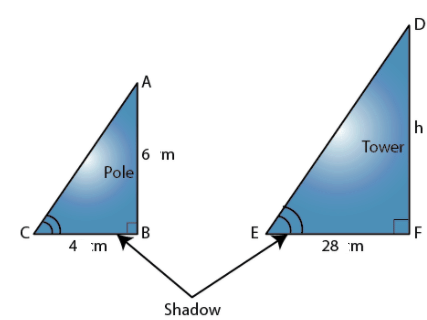
In ΔABC and ΔDFE,

∠C = ∠E (angle of elevation)

∠B = ∠F = 90°

By AA similarity criterion,

ΔABC ~ ΔDFE

We know that the corresponding sides of two similar triangles are proportional.

AB/DF = BC/EF

6/h = 4/28

h = (6 ×28)/4

h = 6 × 7

h = 42

Hence, the height of the tower = 42 m.

Q5. If ΔABC ~ ΔQRP, ar (ΔABC) / ar (ΔPQR) =9/4 , AB = 18 cm and BC = 15 cm, then find PR.

Sol: Given that ΔABC ~ ΔQRP.

ar (ΔABC) / ar (ΔQRP) =9/4

AB = 18 cm and BC = 15 cm

We know that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.

ar (ΔABC) / ar (ΔQRP) = BC²/RP²

9/4 = (15)²/RP²

RP² = (4/9) × 225

PR² = 100

Therefore, PR = 10 cm

Q6. If the areas of two similar triangles are equal, prove that they are congruent.

Sol: Let ΔABC and ΔPQR be the two similar triangles with equal area.

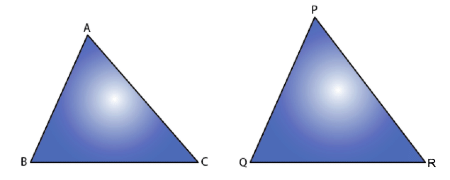
To prove ΔABC ≅ ΔPQR.

Proof:

ΔABC ~ ΔPQR

∴ Area of (ΔABC)/Area of (ΔPQR) = BC²/QR² = AB²/PQ² = AC²/PR²

⇒ BC²/QR² = AB²/PQ² = AC²/PR² = 1 [Since, ar (ΔABC) = ar (ΔPQR)] ⇒ BC²/QR² = 1

⇒ AB²/PQ² = 1

⇒ AC²/PR² = 1

BC = QR

AB = PQ

AC = PR

Therefore, ΔABC ≅ ΔPQR [SSS criterion of congruence]

Q7. O is any point inside a rectangle ABCD as shown in the figure. Prove that OB² + OD² = OA² + OC².

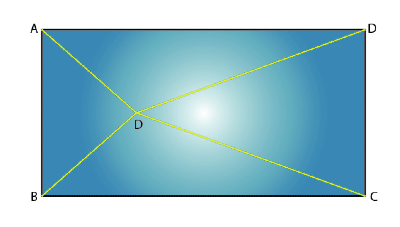
Sol: Through O, draw PQ || BC so that P lies on AB and Q lies on DC.

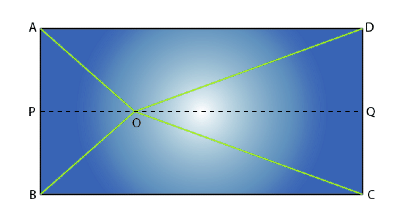
PQ || BC

Therefore, PQ ⊥ AB and PQ ⊥ DC (∠ B = 90° and ∠ C = 90°)

So, ∠ BPQ = 90° and ∠ CQP = 90°

Hence, BPQC and APQD are both rectangles.

By Pythagoras theorem,

In ∆ OPB,

OB² = BP² + OP².....(1)

Similarly,

In ∆ OQD,

OD² = OQ² + DQ².....(2)

In ∆ OQC,

OC² = OQ² + CQ².....(3)

In ∆ OAP,

OA² = AP² + OP².....(4)

Adding (1) and (2),

OB²+ OD² = BP² + OP² + OQ² + DQ²

= CQ² + OP² + OQ² + AP²

(since BP = CQ and DQ = AP)

= CQ² + OQ² + OP² + AP²

= OC² + OA² [From (3) and (4)]

Hence proved that OB² + OD² = OA² + OC².

Q8. Sides of triangles are given below. Determine which of them are right triangles. In case of a right triangle, write the length of its hypotenuse.
(i) 7 cm, 24 cm, 25 cm
(ii) 3 cm, 8 cm, 6 cm

Sol: (i) Given, sides of the triangle are 7 cm, 24 cm, and 25 cm.

Squaring the lengths of the sides of the, we will get 49, 576, and 625.

49 + 576 = 625

(7)² + (24)² = (25)²

Therefore, the above equation satisfies the Pythagoras theorem. Hence, it is a right-angled triangle.

Length of Hypotenuse = 25 cm

(ii) Given, sides of the triangle are 3 cm, 8 cm, and 6 cm.

Squaring the lengths of these sides, we will get 9, 64, and 36.

Clearly, 9 + 36 ≠ 64

Or, 32 + 62 ≠ 82

Therefore, the sum of the squares of the lengths of two sides is not equal to the square of the length of the hypotenuse.

Hence, the given triangle does not satisfy the Pythagoras theorem.

Q9. If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then prove that the other two sides are divided in the same ratio.

Sol: Consider a triangle ΔABCand draw a line PQ parallel to the side BC of ΔABC and intersect the sides AB and AC in P and Q, respectively.

To prove: AP/PB = AQ/QC

Construction:

Join the vertex B of ΔABC to Q and the vertex C to P to form the lines BQ and CP and then drop a perpendicular QN to the side AB and draw PM⊥AC as shown in the given figure.

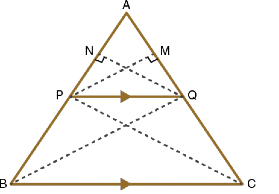
Proof:

Now the area of ∆APQ = 1/2 × AP × QN (Since, area of a triangle= 1/2× Base × Height)

Similarly, area of ∆PBQ= 1/2 × PB × QN

area of ∆APQ = 1/2 × AQ × PM

Also, area of ∆QCP = 1/2 × QC × PM ............ (1)

Now, if we find the ratio of the area of triangles ∆APQand ∆PBQ, we have

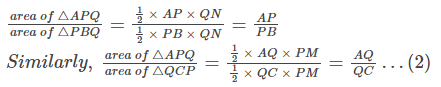
According to the property of triangles, the triangles drawn between the same parallel lines and on the same base have equal areas.

Therefore, we can say that ∆PBQ and QCP have the same area.

area of ∆PBQ = area of ∆QCP ..............(3)

Therefore, from the equations (1), (2) and (3), we can say that,

AP/PB = AQ/QC

Q.10: In the figure, DE || BC. Find the length of side AD, given that AE = 1.8 cm, BD = 7.2 cm and CE = 5.4 cm.

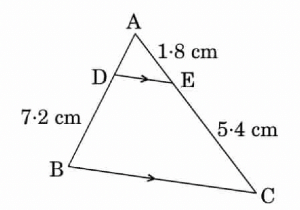
Sol: Given,

DE || BC

AE = 1.8 cm, BD = 7.2 cm and CE = 5.4 cm

By basic proportionality theorem,

AD/DB = AE/EC

AD/7.2 = 1.8/5.4

AD = (1.8 × 7.2)/5.4

= 7.2/4

= 2.4

Therefore, AD = 2.4 cm.

Q.11: Given ΔABC ~ ΔPQR, if AB/PQ = ⅓, then find (ar ΔABC)/(ar ΔPQR).

Sol: Given, 

ΔABC ~ ΔPQR

And

AB/PQ = ⅓, 

We know that The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.

(ar ΔABC)/(ar ΔPQR) = AB²/PQ² = (AB/PQ)² = (⅓)2 = 1/9

Therefore, (ar ΔABC)/(ar ΔPQR) = 1/9

Or

(ar ΔABC) : (ar ΔPQR) = 1 : 9

Q.12: The sides of two similar triangles are in the ratio 7 : 10.  Find the ratio of areas of these triangles.

Sol: Given,

The ratio of sides of two similar triangles = 7 : 10

We know that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.

The ratio of areas of these triangles = (Ratio of sides of two similar triangles)2

= (7)² : (10)²

= 49 : 100

Therefore, the ratio of areas of the given similar triangles is 49 : 100.

Q.13: In an equilateral ΔABC, D is a point on side BC such that BD = (⅓) BC. Prove that 9(AD)² = 7(AB)².

Sol: Given, ABC is an equilateral triangle.

And D is a point on side BC such that BD = (1/3)BC.

Let a be the side of the equilateral triangle and AE be the altitude of ΔABC.

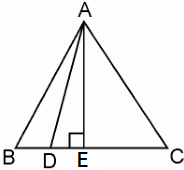
∴ BE = EC = BC/2 = a/2

And, AE = a√3/2

Given, BD = 1/3BC

∴ BD = a/3

DE = BE - BD = a/2 - a/3 = a/6

In ΔADE, by Pythagoras theorem,

AD² = AE² + DE²

= [(a√3)/2]² + (a/6)²

= (3a²/4) + (a²/36)

= (37a² + a²)/36

= (28a²)/36

= (7/9)a²

= (7/9) (AB)²

Therefore, 9(AD)² = 7(AB)^2.

Q.14: Prove that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

Sol: Given: A right-angled triangle ABC, right-angled at B.

To Prove: AC² = AB² + BC²

Construction: Draw a perpendicular BD meeting AC at D.

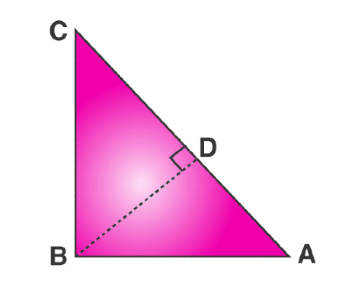
Proof:

In ΔABC and ΔADB,

∠ABC = ∠ADB = 90°

∠A = ∠A → common

Using the AA criterion for the similarity of triangles, 

ΔABC ~ ΔADB 

Therefore, AD/AB = AB/AC

⇒ AB² = AC x AD ......(1)

Considering  ΔABC and ΔBDC from the figure.

C = ∠C  → common

 ∠CDB = ∠ABC = 90°

Using the Angle Angle(AA) criterion for the similarity of triangles, we conclude that,

ΔBDC ~ ΔABC

Therefore, CD/BC = BC/AC

⇒ BC² = AC x CD .....(2)

By adding equation (1) and equation (2), we get:

AB² + BC² = (AC x AD) + (AC x CD)

AB² + BC² = AC (AD + CD) .....(3)

AB² + BC² = AC (AC) {since AD + CD = AC}

AB² + BC² = AC²

Hence proved.

Q.15: In the figure, if PQ || RS, prove that ∆ POQ ~ ∆ SOR.

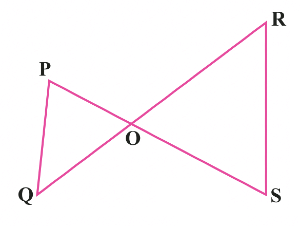
Sol: Given,

PQ || RS

∠P = ∠S (Alternate angles) 

and ∠Q = ∠R 

Also, ∠POQ = ∠SOR (Vertically opposite angles) 

Therefore, ∆ POQ ~ ∆ SOR (by AAA similarity criterion)

Hence proved.