Class 10 Maths Chapter 9 Practice Question Answers - Some Applications of Trigonometry
Q1. Two chimneys 18 m and 13 m high stand upright in the ground. If their feet are 12 m apart, then the distance between their tops is
(a) 5m
(b) 31m
(c) 13m
(d) 18m
Ans: (b)
Sol:
We have to find AC.
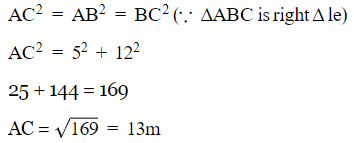
Q2. In the adjoining figure, the positions of observer and object are marked. The angle of depression is ______ .
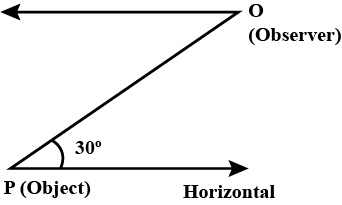
Sol:
The horizontal line of the object and the observer will be parallel to each other.
Thus, the angle of depression of the observer will be equal to the angle of elevation of the object =30∘
Q3. In a prison wall there is a window of 1 metre height, 24 metres from the ground. An observer at a height of 10m from ground, standing at a distance from the wall finds the angle of elevation of the top of the window and the top of the wall to be 45º and 60º respectively. The height of the wall above the window is
(a) 15√3
(b) 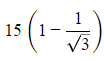
(c) 15(√3-1)
(d) 14(√3-1)
Ans: (d)
Sol:
We can see that , CE=DF=10
Therefore, BC=BE−CE=24−10=14
in △BCD

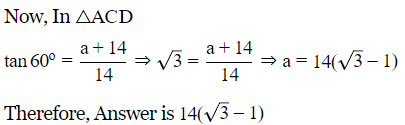
Q4. A pole stands vertically, inside a triangular park ABC. If the angle of elevation of the top of the pole from each corner of the park is same, then the foot of the pole is at the:
(a) centriod
(b) circumcentre
(c) incentre
(d) orthocentre
Ans: (b)
Sol:
If angle of elevation(p) is same from all the vertices then the Pole must be at Equal Distance from each of the vertices which will be =R (Circumradius)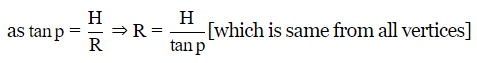
therefore, the pole must be lying on the Circumcenter
Q5. From the top of a tree on one side of a street the angles of elevation and depression of the top and foot of a tower on the opposite side are respectively found to be α and β. If h is the height of the tree, then the height of the tower is:
(a) 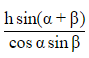
(b) 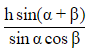
(c) 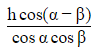
(d) 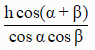
Ans: (a)
Sol:
Let ht +h=H be the total height of tower.
Let x be the distance between tower and tree.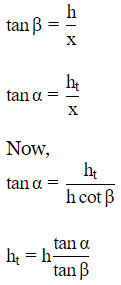
Total height of the tower,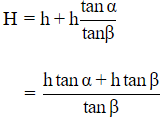
Substituting for tanα and tanβ
we get,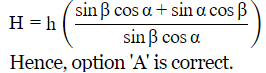
Q6. The angle of elevation of the top of a tower is 30°. If the height of the tower is doubled, then the angle of elevation of its top will
(a) also get doubled
(b) will get halved
(c) will be less than 60 degree
(d) None of these
Ans: (b)
Sol: According to Question: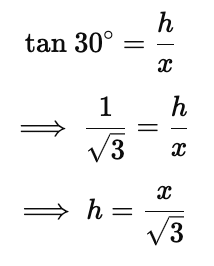
Now, when height of tower is doubled, we get:
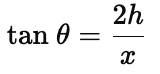
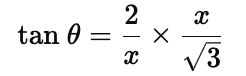
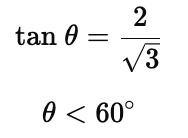
Q7. A straight highway leads to the foot of a tower (AB) of height 50 m. From the top of the tower, the angles of depression of two cars, C and D, standing on the highway are 30º and60º. Find the distance of the second car form the tower to closes integer.
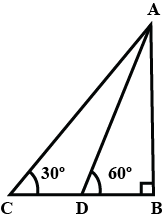
Sol: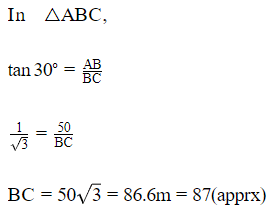
Q8. A person walking 50 metres towards a chimney in a horizontal line. The angle of elevation of its top changes from 30º to 45º . Height of the chimney (in metres) is
(a) 25(3+ √3) m
(b) 50(√3+1) m
(c) 25 (√3+1)m
(d) 25(√3-1) m
Ans: (c)
Sol: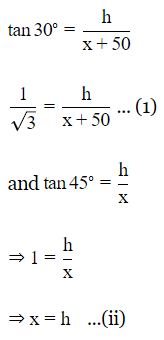
From (i) and (ii), we get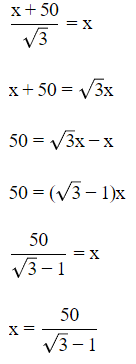
Rationalize the denominator, we get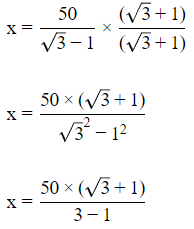
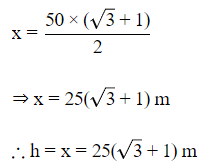
Q9. The angular depression of the top and the foot of a tower as seen from the top of a second tower which is 150m high and standing on the same level as the first are α and β respectively.
If tanα= 3/4 and tanβ= 2/5, the distance between their tops is:
(a) 100 m
(b) 120 m
(c) 110 m
(d) 130 m
Ans: (a)
Sol:
Let AB be the length of 1st tower.
Let BC be the length of 2nd tower.
Here given that CD=150m
BE=CD=150m
From △BCE

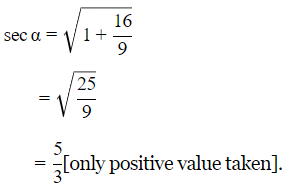
Thus,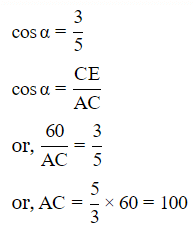
∴ Distance between their tops=100m
Q10. Two pillars of equal height stand on either side of a road way which is 60 metres wide. At a point in the road way between the pillars, the elevation of the top of pillars are 60º and 30º . The height of the pillars is
(a) 15√3m
(b) 15/√3 m
(c) 15 m
(d) 20 m
Ans: (a)
Sol:
Let AB and CD be two towers of equal height 'h'.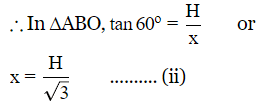
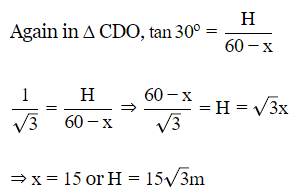
Q11. lf the shadow of a tower is √3 times of its height, the altitude of the sun is
(a) 15º
(b) 30º
(c) 45º
(d) 60º
Ans: (b)
Sol:
Let the height of tower be h.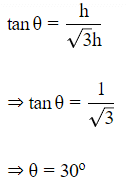
Q12. If the length of the shadow of a pole is equal to the height, of the pole, then the angle of the elevation of the sun is
(a) 30º
(b) 75º
(c) 60º
(d) 45º
Ans: (d)
Sol:
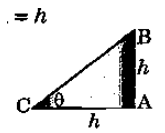
Let AB=h be the pole and let ∠ACB=θ
Let AC be the shadow
Hence, by hypothesis, CA=h
From right angled △BCA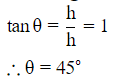
Q13. The shadow of a tower on a level plane is found to be 60 metres longer when the sun's altitude is 30º than that when it is 45º . The height of the tower in metres is
(a) 30 (√3+1)
(b) 30(√3-1)
(c) 30(3+√3)
(d) 30(3-√3)
Ans: (a)
Sol:
Let height of tower be h m.
And length of shadow when sun's altitude is at 30º.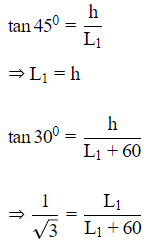
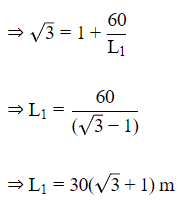
Q14. The shadow of a stick of height 1 meter , when the angle of elevation of the sun is 60, will be
(a) 1/√3 meter
(b) 1/3 meter
(c) √3 meter
(d) 3 meter
Ans: (a)
Sol: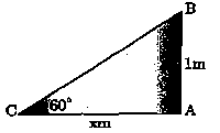
Let AB -1 cm be the stick.
Let AC be the shadow of length x.
from right angled △ACB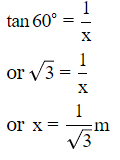
Q15. A man on the top of an observation tower finds an object at an angle of depression 30º. After the object was moved 30 metres in a straight line towards the tower, he finds the angle of depression to be 45º . The distance of the object now from the foot of the tower in metres is
(a) 15√3
(b) 15(√3+1)
(c) 15(√3-1)
(d) 15(2+√3)
Ans: (b)
Sol:
Let the height of the tower be h
⟹AD=h
And d be the initial distance of object from tower.
⟹BD=d
So, CD=d−30
In △ACD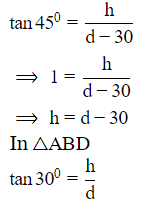
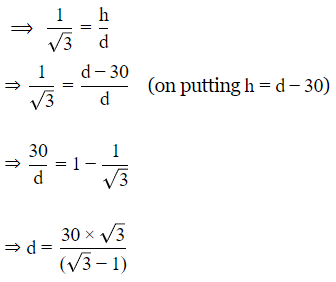
Now, the distance =d−30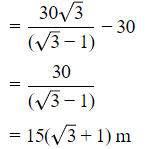
|
127 videos|584 docs|79 tests
|
FAQs on Class 10 Maths Chapter 9 Practice Question Answers - Some Applications of Trigonometry
| 1. What are some real-life applications of trigonometry that a Class 10 student should know? |  |
| 2. How do you solve problems involving angles of elevation and depression? |  |
| 3. Can you explain the sine, cosine, and tangent ratios with examples? |  |
| 4. What is the difference between the angle of elevation and the angle of depression? |  |
| 5. How can trigonometry be used to find the height of a tall building? |  |
















