Short Questions: Electricity

Q1: Sketch a circuit diagram of an electric circuit consisting of a cell, an electric bulb, an ammeter, a voltmeter and a plug key.
Ans: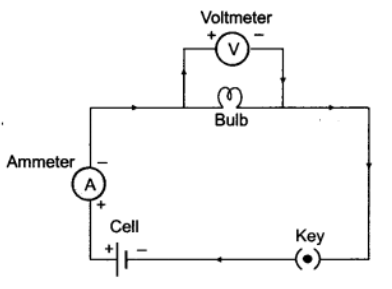 

Q2: Differentiate between Resistance and Resistivity.
Ans: Resistance:

• It is the opposition provided by the atoms of a conductor to the flow of electrons.
• SI unit of resistance is Ω (Ohm).
• Resistance depends on length, area of cross section, material and temperature of conductor.

Resistivity:

• It is the resistance of the conductor of that substance of unit length and unit area of cross section.
• SI unit of Resistivity of Ωm (Ohm-meter).
• Resistivity of substance depends only on the material of substance.

Q3: Distinguish between resistances in series and resistances in parallel.
Ans: Resistances in series:

• If a number of resistances are connected in such a way that the same current flows through each resistance, then the arrangement is called resistances in series.
• The current across each resistance is same.
• The equivalent resistance in series combination is greater than the individual resistances.
• This combination decreases the current.in the circuit.

Resistances in parallel:

• If a number of resistances are connected between two common points in such a way that the potential differences across each of them is the same, then the arrangement is called resistances in parallel.
• The voltage across each resistance is same.
• The equivalent resistance in parallel combination is smaller than each of the individual resistances.
• This combination increases the current in the circuit.

Q4: Nichrome wire is used for making the Ideating elements of electrical appliances like iron, geyser, etc. Give reasons.
Ans: Nichrome wire is used for making the heating elements of electrical appliances like iron, geyser, etc. because:

• Nichrome has a very high resistance due to which it produces a lot of heat on passing current.
• It does not undergo oxidation easily even at high temperature due to which it can be kept red hot.

Q5: A copper wire of resistivity 2.6 × 10^-3 Ωm, has a cross sectional area of 30 × 10^-4 cm³. Calculate the length of this wire required to make a 10 Ω coil.
Ans: Given: R = 10Ω, ρ = 2.6 × 10^-8 Ωm,
To find: l = ?
Formula: R = ρlA
Solution: R = ρlA
∴ ρl = RA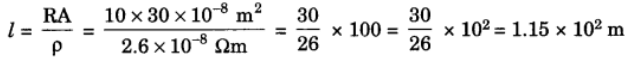


Q6: Two coils of resistance R1 = 3Ω and R2 = 9Ω are connected in series across a battery of potential difference 14 V. Draw the circuit diagram. Find the electrical energy consumed in 1 min in each resistance.
Ans: Given: R₁ = 3Ω, R₂ = 9Ω
R_s = R₁ + R₂ = 9 + 3 = 12 Ω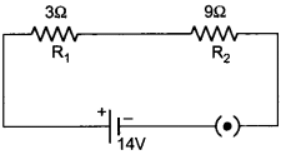

Q7: State the relation between work, charge and potential difference for an electric circuit. Calculate the potential difference between the two terminals of a battery if 100 joules of work is required to transfer 20 coulombs of charge from one terminal of the battery to the other.
Ans: V = W/Q
Here,
V = Potential difference,
W = Work done,
Q = Electric charge
W = 100 J
Q = 20 C
V = WQ=10020 = 5V

Q8: What is an electric circuit? Distinguish between an open and a closed circuit.
Ans:

• Electric circuit: A continuous and closed path of electric current is called an electric circuit.
• Open circuit: A discontinuous circuit through which no current can flow.
• Closed circuit: A circuit without interruption, providing a continuous path through which a current can flow.

Q9: With the help of a diagram, derive the formula for the equivalent resistance of three resistances connected in series.
Ans:
(i) If a number of resistances are connected in such a way that the same current flows through each resistance, then the arrangement is called 'Resistances in Series'.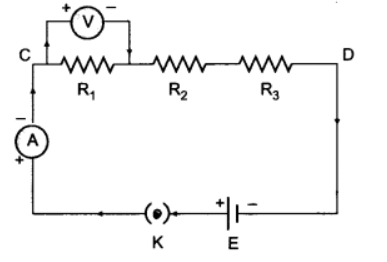
(ii) Let R₁, R₂ and R₃ be three resistances connected in a series combination and let R be their equivalent resistance.
Let V₁, V₂ and V₃ be the potential difference across the resistances R₁, R₂ and R₃ respectively. Let 'V' be the potential differences across the combination. Let 'I' be the current flowing through each resistance.
(iii) According to Ohm's law,
V = IR
Hence, V₁ = IR₁; V₂ = IR₂; V₃ = IR₃
(iv) For series combination of resistances,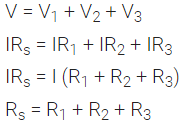

Hence, the equivalent resistance in series (Rs) is equal to the sum of the individual resistances.

Q10: With the help of a diagram, derive the formula for the equivalent resistance of three resistances connected in parallel.
Ans: 1. If a number of resistances are connected between two common points in such a way that the potential difference across each resistance is same, then the arrangement is called 'Resistances in Parallel'.
2. Let R₁, R₂ and R₃ be the three resistances connected in parallel combination between points C and D and let R_p be their equivalent resistance.
Let I₁, I₂ and I₃ be the currents flowing through resistances R₁, R₂ and R₃ respectively.
Let I be the current flowing through the circuit and V be the potential difference of the cell.
3. According to Ohm's law.
I = V/R
Therefore,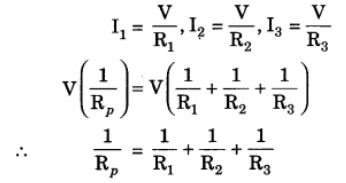

Therefore, the reciprocal of the equivalent resistances in parallel combination is equal to the sum of the reciprocals of the individual resistances.

Q11: What is the better way of connecting lights and other electrical appliances in domestic wiring? Why?
Ans: The better way of connecting lights and other electrical appliances in domestic wiring is parallel connection because of the following advantages:

• In parallel circuit, if one appliance stops working due to some defect, then all other appliances keep working normally.
• In parallel circuit, each electrical appliance has its own switch due to which it can be turned on or off, without affecting other appliances.
• In parallel circuit, each electrical appliance gets the same voltage (220 V) as that of the power supply line.
• In parallel circuit, the overall resistance of the domestic circuit is reduced due to which the current from the power supply is high.

Q12: An electric lamp, whose resistance is 20 Ω, and a conductor of 4 Ω resistance are connected to aft V battery (Fig.).
Calculate (a) the total resistance of the circuit, (b) the current through the circuit, and (c) the potential difference across the electric conductor.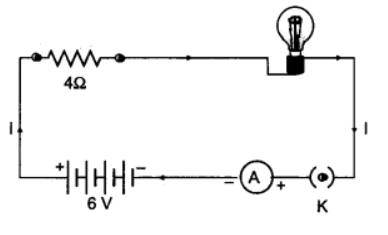

Ans: (a) Resistance of electric lamp, R₁ = 20 W
Resistance of series conductor, R₂ = 4 W
Total resistance in the circuit,
R_s = R₁ + R₂ = 20 Ω + 4 Ω = 24 Ω.
(b) Total potential difference, V = 6 V
By Ohm's law, the current through the circuit is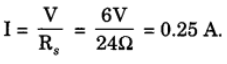

(c) Potential difference across the electric lamp,
V₁ = IR₁ = 0.25 A × 20 Ω = 5 V.
Potential difference across the conductor is
V₂ = IR₂ = 0.25 A × 4 Ω = 1 V.

Q13: A wire has a resistance of 10Ω. It is melted and drawn into a wire of half of its length. Calculate the resistance of the new wire. What is the percentage change in its resistance?
Ans: Given: R₁ = 10 Ω, l₂ = l₁/2
To find: (a) R₂
(b) Percentage change in the resistance (ΔR%).
If volume of the wire remains same in both the cases.

Dividing eq. (iii) by (ii), we get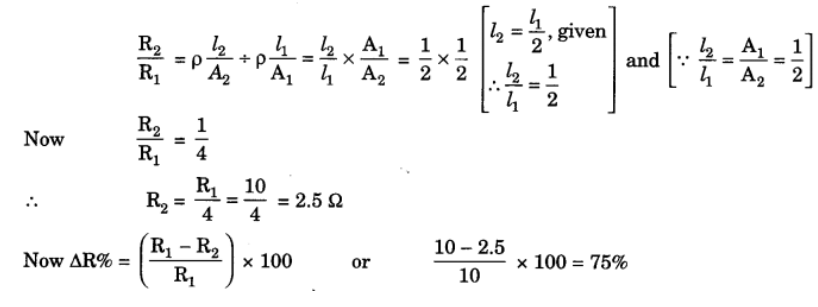


Q14: If, in Figure R₁ = 10 ohms, R₂ = 40 ohms, R₃ = 30 ohms, R₄ = 20 ohms, R_g = 60 ohms and a 12 volt battery is connected to the arrangement, calculate: (a) the total resistance and (b) the total current flowing in the circuit.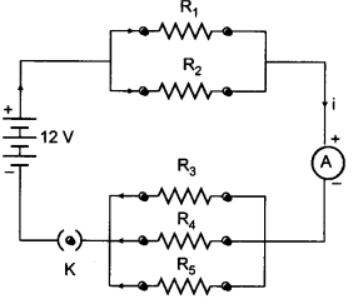

Ans: (a) Let R' be the equivalent resistance of R₁ and R₂. Then,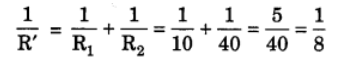

R' = 8Ω
Let R" be the equivalent resistance of R₃, R₄ and R₅. Then,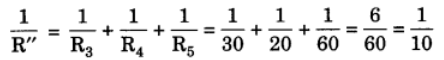

R" = 10 Ω
Total Resistance, R = R' + R" = 8 + 10 = 18 Ω
(b) Current,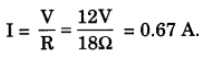


Q15: Two lamps, one rated 60 W at 220 V and other 40 W a 220 V, are connected in parallel to an electric supply at 220 V.
(a) Draw the circuit diagram to show the connections.
(b) Calculate the current drawn from the electric supply.
(c) Calculate the total energy consumed by the two lamp together when they operate for one hour.
Ans: (a) The required circuit diagram is shown below: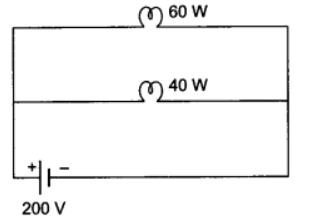

(b) Total power of the two lamps = 60 + 40 = 100 W
Applied Voltage, V = 220 V
Current drawn from the electric supply,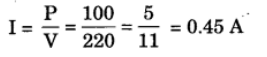

(c) Total energy consumed by the lamp in one hour = 60W × 1h + 40W × 1h = 100 Wh = 0.1 kWh.