Q1: The x-coordinate of a point P is twice its y-coordinate. If P is equidistant from Q (2, -5) and R(-3, 6), find the coordinates of P.
Ans:
Let the point P be (2k, k), Q(2,-5), R(-3, 6)
 PQ = PR …Given
PQ = PR …Given
PQ2 = PR2 …[Squaring both sides
(2k – 2)2 + (k + 5)2 = (2k + 3)2 + (k – 6)2 …Given
4k2 + 4 – 8k + k2 + 10k + 25 = 4k2 + 9 + 12k + k2 – 12k + 36
⇒ 2k + 29 = 45
⇒ 2k = 45 – 29
⇒ 2k = 16
⇒ k = 8
Hence coordinates of point P are (16, 8).
Q2: Find the area of a parallelogram ABCD if three of its vertices are A(2, 4), B(2 + √3, 5) and C(2, 6).
Ans:


Since diagonal of a ||gm divides it into two equal areas.
Area of ABCD (||gm) = 2(Area of ∆ABC)
= 2√3 sq. units
Q3: Find the coordinates of a point P, which lies on the line segment joining the points A(-2, -2) and B(2, -4) such that AP = 3/7AB.
Ans:


Q4: If P(2, 4) is equidistant from Q(7, 0) and R(x, 9), find the values of x. Also find the distance P.
Ans:
 PQ = PR …[Given]
PQ = PR …[Given]
PQ2 = PR2 … [Squaring both sides
∴ (7 – 2)2 + (0 – 4)2 = (x – 2)2 + (9 – 4)2
⇒ 25 + 16 = (x – 2)2 + 25
⇒ 16 = (x – 2)2
⇒ ±4 = x – 2 …[Taking sq. root of both sides
⇒ 2 ± 4 = x
⇒ x = 2 + 4 = 6 or x = 2 – 4 = -2

Q5: Find the value of k, if the points P(5, 4), Q(7, k) and R(9, – 2) are collinear.
Ans:
Given points are P(5, 4), Q(7, k) and R(9, -2).
x1 (y2 – y3) + x2(y3 – y1) + x3(y1 – y2) = 0 …[∵ Points are collinear
∴ 5 (k + 2) + 7 (- 2 – 4) + 9 (4 – k) = 0
5k + 10 – 14 – 28 + 36 – 9k = 0
4 = 4k
∴ k = 1
Q6: If the points A(1, -2), B(2, 3), C(-3, 2) and D(-4, -3) are the vertices of parallelogram ABCD, then taking AB as the base, find the height of this parallelogram.
Ans:






Q7: The three vertices of a parallelogram ABCD are A(3, 4), B(-1, -3) and C(-6, 2). Find the coordinates of vertex D and find the area of ABCD.
Ans:



Q8: If (3, 3), (6, y), (x, 7) and (5, 6) are the vertices of a parallelogram taken in order, find the values of x and y.
Ans:
Let A (3, 3), B (6, y), C (x, 7) and D (5, 6).


Q9: Find the ratio in which the point P(x, 2) divides the line segment joining the points A(12, 5) and B(4, -3). Also, find the value of x.
Ans:


Q10: Point P(x, 4) lies on the line segment joining the points A(-5, 8) and B(4, -10). Find the ratio in which point P divides the line segment AB. Also find the value of x.
Ans:


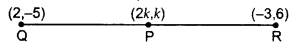 PQ = PR …Given
PQ = PR …Given



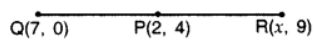 PQ = PR …[Given]
PQ = PR …[Given]








































