Class 10 Maths Chapter 10 Question Answers - Circles
Q1: Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
Ans: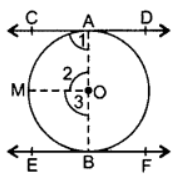 Given: CD and EF are two C parallel tangents at points A and B of a circle with centre O.
Given: CD and EF are two C parallel tangents at points A and B of a circle with centre O.
To prove: AB passes through centre O or AOB is diameter of the circle.
Const.: Join OA and OB. Draw OM || CD.
Proof: ∠1 = 90° … (i)
…[∵ Tangent is I to the radius through the point of contact
OM || CD
∴ ∠1 + ∠2 = 180° …(Co-interior angles
90° + ∠2 = 180° …[From (i)
∠2 = 180° – 90o = 90°
Similarly, ∠3 = 90°
∠2 + ∠3 = 90° + 90° = 180°
∴ AOB is a straight line.
Hence AOB is a diameter of the circle with centre O.
∴ AB passes through centre 0.
Q2: In the figure, the sides AB, BC and CA of triangle ABC touch a circle with centre o and radius r at P, Q and R. respectively.
Prove that:
(i) AB + CQ = AC + BQ
(ii) Area (AABC) = 1/2 (Perimeter of ∆ABC ) × r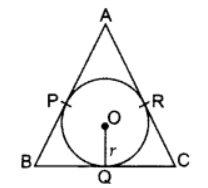
Ans: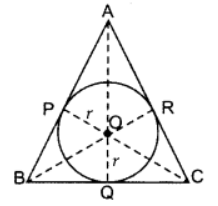 Part I:
Part I:
Proof: AP = AR …(i)
BP = BQ … (ii)
CQ = CR … (iii)
Adding (i), (ii) & (iii)
AP + BP + CQ
= AR + BQ + CR
AB + CQ = AC + BQ
Part II: Join OP, OR, OQ, OA, OB and OC
Proof: OQ ⊥ BC; OR ⊥ AC; OP ⊥ AB
ar(∆ABC) = ar(∆AOB) + ar(∆BOC) + ar (∆AOC)
Area of (∆ABC)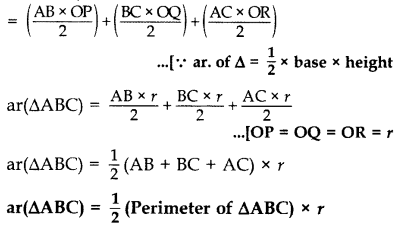
Q3: In the figure, l and m are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line I at D and m at E. Prove that ∠DOE = 90°.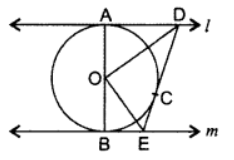 Ans: Proof: Let I be XY and m be XY’
Ans: Proof: Let I be XY and m be XY’
∠XDE + ∠X’ED = 180° … [Consecutive interior angles]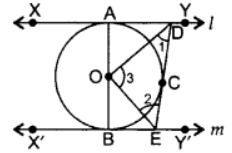
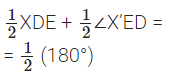
= ∠1 + ∠2 = 90° …[OD is equally inclined to the tangents
In ∆DOE, ∠1 + ∠2 + 23 = 180° …[Angle-sum-property of a ∆
90° + 23 = 180°
⇒ ∠3 = 180° – 90o = 90°
∴ ∠DOE = 90° …(proved)
Q4: In the figure, l and m are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line I at D and m at E. Prove that ∠DOE = 90°. Ans: Proof: Let I be XY and m be XY’
Ans: Proof: Let I be XY and m be XY’
∠XDE + ∠X’ED = 180° … [Consecutive interior angles]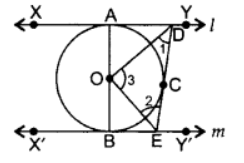
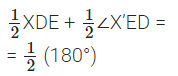
= ∠1 + ∠2 = 90° …[OD is equally inclined to the tangents
In ∆DOE, ∠1 + ∠2 + 23 = 180° …[Angle-sum-property of a ∆
90° + 23 = 180°
⇒ ∠3 = 180° – 90o = 90°
∴ ∠DOE = 90° …(proved)
Q5: Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
Ans: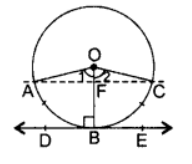 B is the mid point of arc (ABC)
B is the mid point of arc (ABC)
OA = OC …[Radius
OF = OF …[Common
∴ ∠1 = ∠2 …[Equal angles opposite equal sides
∴ ∆OAF = ∆OCF (SAS)
∴ ∠AFO = ∠CFO = 90° …[c.p.c.t
⇒ ∠AFO = ∠DBO = 90° …[Tangent is ⊥to the radius through the point of contact
But these are corresponding angles,
∴ AC || DE
Q6: Prove that the lengths of tangents drawn from an external point to a circle are equal.
Ans: Given: PT and PS are tangents from an external point P to the circle with centre O.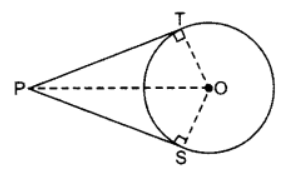 To prove: PT = PS
To prove: PT = PS
Const.: Join O to P,
T & S
Proof: In ∆OTP and
∆OSP,
OT = OS …[radii of same circle
OP = OP …[circle
∠OTP – ∠OSP …[Each 90°]
∴ AOTP = AOSP …[R.H.S]
PT = PS …[c.p.c.t]
Q7: Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
Ans: 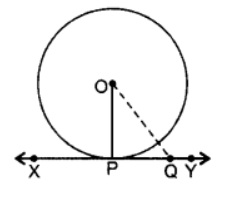 Given: XY is a tangent at point P to the circle with centre O.
Given: XY is a tangent at point P to the circle with centre O.
To prove: OP ⊥ XY
Const.: Take a point Q on XY other than P and join to OQuestion
Proof: If point Q lies inside the circle, then XY will become a secant and not a tangent to the circle.
∴ OQ > OP
This happens with every point on the line XY except the point P.
OP is the shortest of all the distances of the point O to the points of XY
∴ OP ⊥ XY … [Shortest side is ⊥]
Q8: 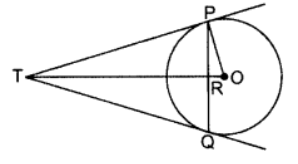 In the above figure, PQ is a chord of length 16 cm, of a circle of radius 10 cm. The tangents at P and Q intersect at a point T. Find the length of TP.
In the above figure, PQ is a chord of length 16 cm, of a circle of radius 10 cm. The tangents at P and Q intersect at a point T. Find the length of TP.
Ans:
TP = TQuestion .. [Tangents drawn from an external point]
∆TPQ is an isosceles ∆ and TO is the bisector of ∠PTQ ,
OT ⊥ PQ …[Tangent is ⊥ to the radius through the point of contact
∴ OT bisects PQ
∴ PR = RQ = 16 = 8 cm …[Given]
In rt. ∆PRO,
PR2 + RO2 = PO2 … [Pythagoras’ theorem]
82 + RO2 = (10)2
RO2 = 100 – 64 = 36
∴ RO = 6 cm
Let TP = x cm and TR = y cm
Then OT = (y + 6) cm
In rt. ∆PRT, x2 = y2 + 82 …(i) …[Pythagoras’ theorem]
In rt. ∆OPT,
OT2 = TP2 + PO2 …(Pythagoras’ theorem]
(y + 6)2 = x2 + 102
y2 + 12y + 36 = y2 +64 + 100 …[From (i)]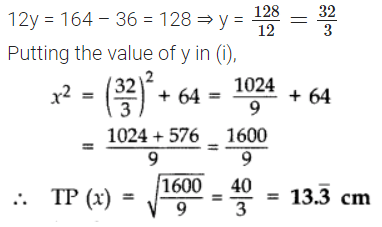
Q9: In the figure, tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQuestion Find ∠RQS.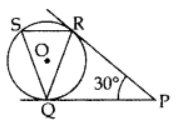 Ans:
Ans:
PR = PO …[∵ Tangents drawn from an external point are equal
⇒ ∠PRQ = ∠PQR …[∵ Angles opposite equal sides are equal
In ∆PQR, 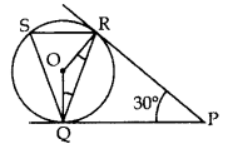 ⇒ ∠PRQ + ∠RPQ + ∠POR = 180°…[∆ Rule]
⇒ ∠PRQ + ∠RPQ + ∠POR = 180°…[∆ Rule]
⇒ 30° + 2∠PQR = 180° 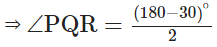
= 75°
⇒ SR || QP and QR is a transversal
∵ ∠SRQ = ∠PQR … [Alternate interior angle
∴ ∠SRO = 75° …..[Tangent is I to the radius through the point of contact
⇒ ∠ORP = 90°
∴ ∠ORP = ∠ORQ + ∠QRP
90° = ∠ORQ + 75°
∠ORQ = 90° – 75o = 150
Similarly, ∠RQO = 15°
In ∆QOR,
∠QOR + ∠QRO + ∠OQR = 180° …[∆ Rule
∴∠QOR + 15° + 15° = 180°
∠QOR = 180° – 30° = 150° 
In ARSQ, ∠RSQ + ∠QRS + ∠RQS = 180° … [∆ Rule]
∴ 75° + 75° + ∠RQS = 180°
∠RQS = 180° – 150° = 30°
Q10: In the figure, O is the centre of a circle of radius 5 cm. T is a point such that OT = 13 cm and OT intersects circle at E. If AB is a tangent to the circle at E, find the length of AB, where TP and TQ are two tangents to the circle.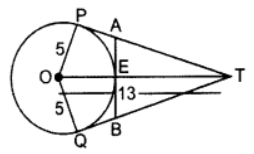 Ans:
Ans:
∠OPT = 90° …[Tangent is ⊥ to the radius through the point of contact
We have, OP = 5 cm, OT = 13 cm
In rt. ∆OPT,
OP2 + PT2 = OT? …[Pythagoras’ theorem
⇒ (5)2 + PT2 = (13)2
⇒ PT2 = 169 – 25 = 144 cm
⇒ PT = √144144−−−√
= 12 cm
OP = OQ = OE = 5 cm … [Radius of the circle
ET = OT – OE
= 13 – 5 = 8 cm
Let, PA = x cm, then AT = (12 – x) cm
PA = AE = x cm …[Tangent drawn from an external point
In rt. ∆AET,
AE2 + ET2 = AT2 …(Pythagoras’ theorem
⇒ x2 + (8)2 = (12 – x)2
⇒ x2 + 64 = 144 + x2 – 24x
⇒ 24x = 144 – 64 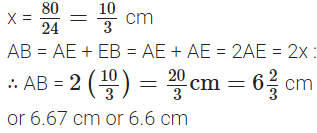
|
127 videos|674 docs|84 tests
|
FAQs on Class 10 Maths Chapter 10 Question Answers - Circles
| 1. What is the formula for the area of a circle? |  |
| 2. How do you find the circumference of a circle? |  |
| 3. What is the relationship between the radius and diameter of a circle? |  |
| 4. How do you calculate the length of an arc in a circle? |  |
| 5. What is the definition of a tangent to a circle? |  |





















