Class 9 Maths Chapter 10 Question Answers - Heron’s Formula
Q1: Find the area of a triangle whose sides are 11 m, 60 m and 61 m.
Ans:
Let a = 11 m, b = 60 m and c = 61 m :
Firstly, to calculate semi perimeter (s)
∴ a + b + c2 = 11 + 60 + 612 = 1322 = 66 m
Now,
s − a = 66 − 11 = 55 m
s − b = 66 − 60 = 6 m
s − c = 66 − 61 = 5 m
∴ Area = √[s(s − a)(s − b)(s − c)]
= √[66(55)(6)(5)]
= √108900
= 330 m2.
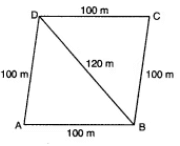
Q2: Suman has a piece of land, which is in the shape of a rhombus. She wants her two sons to work on the land and produce different crops. She divides the land in two equal parts by drawing a diagonal. If its perimeter is 400 m and one of the diagonals is of length 120 m, how much area each of them will get for his crops ?
Ans:
Here, perimeter of the rhombus is 400 m.
∴ Side of the rhombus = 400/4 = 100 m
Let diagonal BD = 120 m and this diagonal divides the rhombus ABCD into two equal parts.
∴ s = 100 + 120 + 1002 = 3202 = 160
∴Area of ΔABD = √[s(s − a)(s − b)(s − c)]
= √[160(160 − 100)(160 − 100)(160 − 120)]
= √[160 × 60 × 60 × 40]
= 80 × 60 = 4800 m2
Hence, area of land allotted to two sons for their crops is 4800 m2 each.
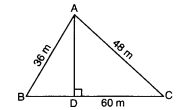
Q3: The perimeter of a triangular field is 144 m and its sides are in the ratio 3:4:5. Find the length of the perpendicular from the opposite vertex to the side whose length is 60 m.
Ans:
Let the sides of the triangle be 3x, 4x and 5x
∴ The perimeter of the triangular field = 144 m
⇒ 3x + 4x + 5x = 144m
⇒ 12x = 144m⇒ x = 14412 = 12 m
Sides of the triangle are: (3 × 12 = 36) m, (4 × 12 = 48) m, (5 × 12 = 60) m
∴ s = a + b + c2 = 36 + 48 + 602 = 1442 = 72 m
Area of ΔABC = √[s(s − a)(s − b)(s − c)] (using Heron's formula)
= √[72(72 − 36)(72 − 48)(72 − 60)]
= √[72 × 36 × 24 × 12]
= √746496 = 864 m2
∴ Also, Area (ΔABC) = 12 × AD × BC (Using the formula for area)
= 1 2 × AD × 60 = 30 x AD
∴ 30 x AD = 864
AD = 86430 = 28.8 m
Q4:Find the area of the triangle whose perimeter is 180 cm and two of its sides are of lengths 80 cm and 18 cm. Also, calculate the altitude of the triangle corresponding to the shortest side.
Ans:
Perimeter of given triangle = 180 cm
Two sides are 18 cm and 80 cm
∴ Third side = 180 – 18 – 80 = 82 cm
s = 1802 = 90 cm
Area of triangle using Heron's Formula:
Area = √[s(s − a)(s − b)(s − c)]
= √[90(90 − 18)(90 − 80)(90 − 82)]
= √[90 × 72 × 10 × 8]
= √518400 = 720 cm2
Use area formula to calculate height (h):
12 × base × height = Area
12 × 18 × h = 720
9 × h = 720
h = 7209 = 80 cmHence, area of triangle is 720 cm2and altitude of the triangle corresponding to the shortest side is 80 cm.
Q5: Calculate the area of the shaded region.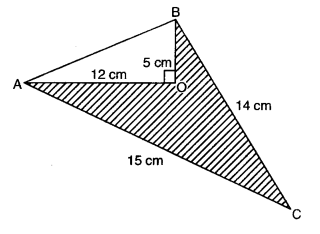
Ans:
Area of ΔAOB:
Area = 12 × OA × OB
= 12 × 12 × 5 = 30 cm2
Calculate AB:
AB2 = OA2 + OB2
= 122 + 52 = 144 + 25 = 169
AB = √169= 13 cmArea of ΔABC:
a = BC = 14 cm, b = CA = 15 cm, c = AB = 13 cm
s = a + b + c2 = 14 + 15 + 132 = 422 = 21 cmUsing Heron's Formula:
Area = √[s(s − a)(s − b)(s − c)]
= √[21(21 − 14)(21 − 15)(21 − 13)]
= √[21 × 7 × 6 × 8]
= √[3 × 7 × 7 × 2 × 3 × 2 × 2 × 2]
= 2 × 2 × 3 × 7 = 84 cm2
Area of shaded region = Area of ∆ABC – Area of ∆AOB
= 84 cm2– 30 cm2= 54 cm2
Q6: The sides of a triangular park are 8 m, 10 m and 6 m respectively. A small circular area of diameter 2 m is to be left out and the remaining area is to be used for growing roses. How much area is used for growing roses ? (use n = 3.14)
Ans:
The sides of the triangular park are 8 m, 10 m and 6 m.
∴ s = a + b + c2 = 8 + 10 + 62 = 242 = 12 m
Area of the park using Heron's Formula:
Area = √[s(s − a)(s − b)(s − c)]
= √[12(12 − 8)(12 − 10)(12 − 6)]
= √[12 × 4 × 2 × 6]
= √[2 × 2 × 3 × 2 × 2 × 2 × 3]
= 2 × 2 × 2 × 3 = 24 m2
Radius of the circle = 2/2 = 1 m
Area of the circle = πr2 = 3.14 × 1 × 1 = 3.14 m2
∴ Area to be used for growing roses = Area of the park – area of the circle
⇒ 24 – 3.14 = 20.86 m2
Q7: The Triangular garden has sides 40 m, 60 m, and 80 m. A landscaping company needs to install a pond in the center of the garden. How much area will the company need to clear for the pond?
Ans: Given, The sides of the triangular garden are 40 m, 60 m, and 80 m.
The semi-perimeter, 40+ 60 +802
= 90 mUsing Heron's formula, we have:
Area of triangle = √[s(s − a)(s − b)(s − c)]
= √[90(90 − 40)(90 − 60)(90 − 80)]
= √[90 × 50 × 30 × 10] m2
= √1350000 m2
= 1161.9 m2
Q8: The sides of a triangle are in the ratio of 12: 17: 25 and its perimeter is 540 cm. Find its area.
Ans: Given, Ratio of the sides of the triangle is 12: 17: 25
Let the sides of triangle be 12x, 17x and 25x
Given, perimeter of the triangle = 540 cm
12x + 17x + 25x = 540 cm
⇒ 54x = 540cm
So, x = 10
Thus, the sides of the triangle are:
12 x 10 = 120 cm
17 x 10 = 170 cm
25 x 10 = 250 cm
Semi perimeter, s = 5402 = 270 cm
Using Heron’s formula,
Area of the triangle = √[s (s-a) (s-b) (s-c)]
= √[270 (270 – 120) (270 – 170) (270 – 250)]
= √(270 x 150 x 100 x 20)
= 9000 cm2
Q9: Find the area of a triangle whose two sides are 14 cm and 12 cm, respectively, and the perimeter is 38 cm.
Ans:
Given Two sides of the triangle are 14 cm and 12 cm, and the perimeter is 38 cm.
Let the third side be c.
The perimeter of the triangle is given as 38 cm:
a + b + c = 38
14 + 12 + c = 38
c = 38 - 26 = 12 cm
The semi-perimeter s is calculated as:
s = 382 = 19 cm
Using Heron’s formula:
Area = √[s(s - a)(s - b)(s - c)]
Substitute the values:
Area = √[19(19 - 14)(19 - 12)(19 - 12)]
Area = √[19 × 5 × 7 × 7]
Area = √[4655]
The area of the triangle is approximately 68.22 cm².
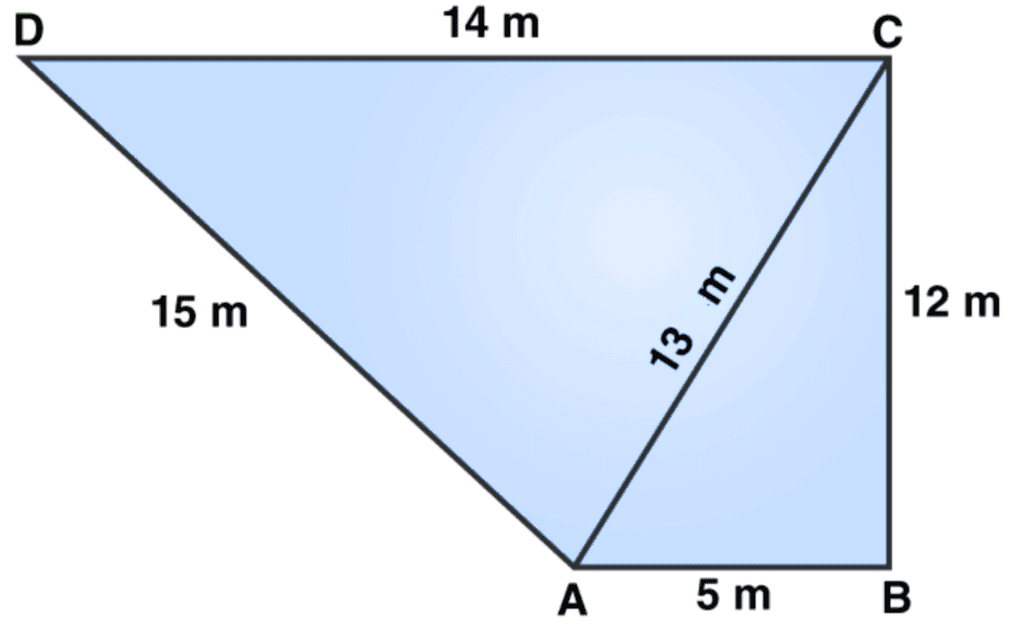
Q10: The sides of a quadrilateral, taken in order as 5, 12, 14, and 15 meters, respectively, and the angle contained by the first two sides is a right angle. Find its area.
Ans:
Here, AB = 5 m, BC = 12 m, CD =14 m and DA = 15 m
Join the diagonal AC.
Now, the area of △ABC = 1/2 ×AB×BC
= 1/2×5×12 = 30
The area of △ABC is 30 m2
In △ABC, (right triangle).
From Pythagoras theorem,
AC2 = AB2 + BC2
AC2 = 52 + 122
AC2 = 25 + 144 = 169
or AC = 13 m
Now in △ADC,
All sides are known, apply Heron’s Formula:
Area of triangle = √[s(s − a)(s − b)(s − c)]
Semi-Perimeter, s = a + b + c2
Where: a, b, and c are the sides of the triangle.
Perimeter of △ADC = 2s = AD + DC + AC
2s = 15 m +14 m +13 m
s = 21 m
Area of triangle ADC = √[21 × (21 − 13) × (21 − 14) × (21 − 15)]
Area of triangle ADC = √[21 × 8 × 7 × 6]
Area of △ADC = 84 m2
Area of quadrilateral ABCD = Area of △ABC + Area of △ADC
= (30 + 84) m2
= 114 m2
|
40 videos|560 docs|57 tests
|
FAQs on Class 9 Maths Chapter 10 Question Answers - Heron’s Formula
| 1. What is Heron’s Formula and how is it derived? |  |
| 2. How do you calculate the semi-perimeter of a triangle using Heron’s Formula? |  |
| 3. Can Heron’s Formula be used for all types of triangles? |  |
| 4. What are some practical applications of Heron’s Formula? |  |
| 5. How do you use Heron’s Formula to find the area of a triangle with sides 7 cm, 8 cm, and 9 cm? |  |