Class 9 Maths Question Answers - Circles
Q1: Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are 90° – (½)A, 90° – (½)B and 90° – (½)C.
Sol: Consider the following diagram: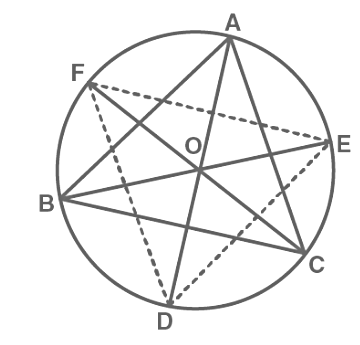 Here, ABC is inscribed in a circle with center O and the bisectors of ∠A, ∠B and ∠C intersect the circumcircle at D, E and F respectively.
Here, ABC is inscribed in a circle with center O and the bisectors of ∠A, ∠B and ∠C intersect the circumcircle at D, E and F respectively.
Now, join DE, EF and FD
As angles in the same segment are equal, so,
∠FDA = ∠FCA ————-(i)
∠FDA = ∠EBA ————-(i)
Adding equations (i) and (ii) we have,
∠FDA + ∠EDA = ∠FCA + ∠EBA
Or, ∠FDE = ∠FCA + ∠EBA = (½)∠C + (½)∠B
We know, ∠A + ∠B + ∠C = 180°
So, ∠FDE = (½)[∠C + ∠B] = (½)[180° – ∠A]
⇒ ∠FDE = [90 – (∠A/2)]
In a similar way,
∠FED = [90 – (∠B/2)]
And,
∠EFD = [90 – (∠C/2)]
Q2: Prove that the circle drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.
Sol: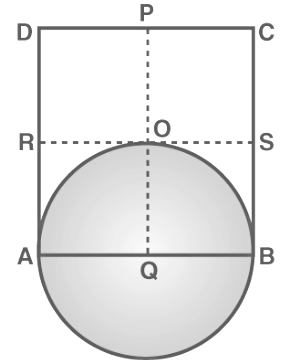 To prove: A circle drawn with Q as centre, will pass through A, B and O (i.e. QA = QB = QO)
To prove: A circle drawn with Q as centre, will pass through A, B and O (i.e. QA = QB = QO)
Since all sides of a rhombus are equal,
AB = DC
Now, multiply (½) on both sides
(½)AB = (½)DC
So, AQ = DP
⇒ BQ = DP
Since Q is the midpoint of AB,
AQ= BQ
Similarly,
RA = SB
Again, as PQ is drawn parallel to AD,
RA = QO
Now, as AQ = BQ and RA = QO we have,
QA = QB = QO (hence proved).
Q3: If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lies on the third side.
Sol: First, draw a triangle ABC and then two circles having a diameter as AB and AC respectively.
We will have to now prove that D lies on BC and BDC is a straight line.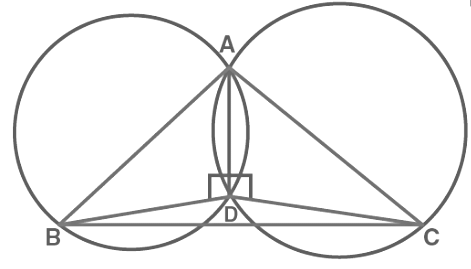
Proof:
As we know, angle in the semi-circle are equal
So, ∠ADB = ∠ADC = 90°
Hence, ∠ADB + ∠ADC = 180°
∴ ∠BDC is a straight line.
So, it can be said that D lies on the line BC.
Q4: ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70°, ∠BAC is 30°, find ∠BCD. Further, if AB = BC, find ∠ECD.
Sol: Consider the following diagram.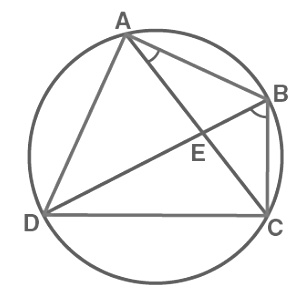 Consider the chord CD,
Consider the chord CD,
As we know, angles in the same segment are equal.
So, ∠CBD = ∠CAD
∴ ∠CAD = 70°
Now, ∠BAD will be equal to the sum of angles BAC and CAD.
So, ∠BAD = ∠BAC + ∠CAD
= 30° + 70°
∴ ∠BAD = 100°
As we know, the opposite angles of a cyclic quadrilateral sum up to 180 degrees.
So,
∠BCD + ∠BAD = 180°
Since, ∠BAD = 100°
So, ∠BCD = 80°
Now consider the ΔABC.
Here, it is given that AB = BC
Also, ∠BCA = ∠CAB (Angles opposite to equal sides of a triangle)
∠BCA = 30°
also, ∠BCD = 80°
∠BCA + ∠ACD = 80°
So, ∠ACD = 50° and,
∠ECD = 50°
Q5: In Figure, ∠PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠OPR.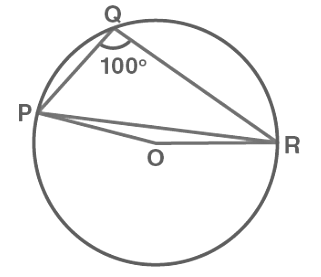 Sol: Since angle which is subtended by an arc at the centre of the circle is double the angle subtended by that arc at any point on the remaining part of the circle.
Sol: Since angle which is subtended by an arc at the centre of the circle is double the angle subtended by that arc at any point on the remaining part of the circle.
So, the reflex ∠POR = 2 × ∠PQR
We know the values of angle PQR as 100°
So, ∠POR = 2 × 100° = 200°
∴ ∠POR = 360° – 200° = 160°
Now, in ΔOPR,
OP and OR are the radii of the circle
So, OP = OR
Also, ∠OPR = ∠ORP
Now, we know sum of the angles in a triangle is equal to 180 degrees
So,
∠POR + ∠OPR + ∠ORP = 180°
⇒ ∠OPR + ∠OPR = 180° – 160°
As ∠OPR = ∠ORP
⇒ 2∠OPR = 20°
Thus, ∠OPR = 10°
Q6: In any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
Sol: Consider this diagram: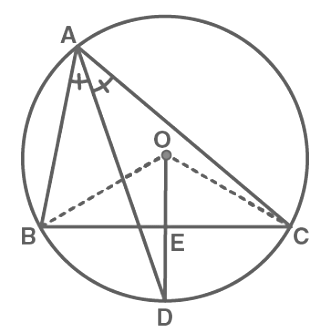 Given: In ∆ABC, AD is the angle bisector of ∠A and OD is the perpendicular bisector of BC, intersecting each other at point D.
Given: In ∆ABC, AD is the angle bisector of ∠A and OD is the perpendicular bisector of BC, intersecting each other at point D.
To Prove: D lies on the circle
Construction: Join OB and OC
Proof:
BC is a chord of the circle.
The perpendicular bisector will pass through centre O of the circumcircle.
∴ OE ⊥ BC & E is the midpoint of BC
Chord BC subtends twice the angle at the centre, as compared to any other point.
BC subtends ∠BAC on the circle & BC subtends ∠BOC on the centre
∴ ∠BAC = 1/2 ∠ BOC
In ∆ BOE and ∆COE,
BE = CE (OD bisects BC)
∠BEO = ∠CEO (Both 90°, as OD ⊥ BC)
OE = OE (Common)
∴ ∆BOE ≅ ∆COE (SAS Congruence rule)
∴ ∠BOE = ∠COE (CPCT)
Now,
∠BOC = ∠BOE + ∠COE
∠BOC = ∠BOE + ∠BOE
∠BOC = 2 ∠BOE …(2)
AD is angle bisector of ∠A
∴ ∠BAC = 2∠BAD
From (1)
∠BAC = 1/2 ∠BOC
2 ∠BAD = 1/2 (2∠BOE)
2 ∠BAD = ∠BOE
∠BAD = 1/2 ∠BOE
BD subtends ∠BOE at centre and half of its angle at Point A.
Hence, BD must be a chord.
∴ D lies on the circle.
Q7: Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6, find the radius of the circle.
Sol: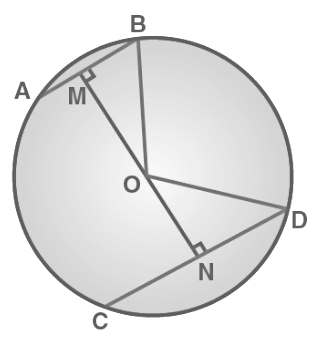 Here, OM ⊥ AB and ON ⊥ CD. is drawn and OB and OD are joined.
Here, OM ⊥ AB and ON ⊥ CD. is drawn and OB and OD are joined.
As we know, AB bisects BM as the perpendicular from the centre bisects the chord.
Since AB = 5 so,
BM = AB/2
Similarly, ND = CD/2 = 11/2
Now, let ON be x.
So, OM = 6− x.
Consider ΔMOB,
OB2 = OM2 + MB2
Or,
OB2 = 36 + x2 – 12x + 25/4 ……(1)
Consider ΔNOD,
OD2 = ON2 + ND2
Or,
OD2 = x2 + 121/4 ……….(2)
We know, OB = OD (radii)
From eq. (1) and eq. (2) we have;
36 + x2 -12x + 25/4 = x2 + 121/4
12x = 36 + 25/4 – 121/4
12x = (144 + 25 -121)/4
12x = 48/4 = 12
x = 1
Now, from eq. (2) we have,
OD2 = 11 + (121/4)
Or OD = (5/2) × √5
Q8: If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
Sol: Construction-Consider a trapezium ABCD with AB||CD and BC = AD.
Draw AM ⊥CD and BN ⊥ CD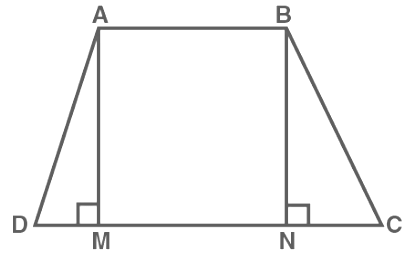 In ∆AMD and ∆BNC;
In ∆AMD and ∆BNC;
AD = BC (Given)
∠AMD = ∠BNC (90°)
AM =BN (perpendiculars between parallel lines)
∆AMD = ∆BNC (By RHS congruency)
∆ADC = ∆BCD (By CPCT rule) …….(i)
∠BAD and ∠ADC are on the same side of transversal AD.
∠BAD + ∠ADC = 180° ……(ii)
∠BAD + ∠BCD = 180° (by equation (i))
Since, the opposite angles are supplementary, therefore, ABCD is a cyclic quadrilateral.
Q9: In Figure, ∠ABC = 69°, ∠ ACB = 31°, find ∠BDC.
Sol:
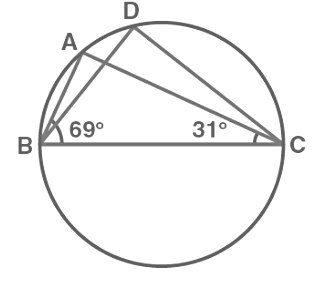 As we know, angles in the segment of the circle are equal so,
As we know, angles in the segment of the circle are equal so,
∠BAC = ∠BDC
Now in the In ΔABC, sum of all the interior angles will be 180°
So, ∠ABC + ∠BAC + ∠ACB = 180°
Now, by putting the values,
∠BAC = 180° – 69° – 31°
So, ∠BAC = 80°
Q10: A circular park of radius 20m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.
Sol: First, draw a diagram according to the given statements. The diagram will look as follows.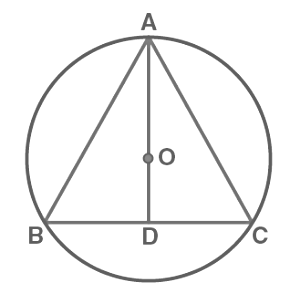 Here the positions of Ankur, Syed and David are represented as A, B and C respectively. Since they are sitting at equal distances, the triangle ABC will form an equilateral triangle.
Here the positions of Ankur, Syed and David are represented as A, B and C respectively. Since they are sitting at equal distances, the triangle ABC will form an equilateral triangle.
AD ⊥ BC is drawn. Now, AD is median of ΔABC and it passes through the centre O.
Also, O is the centroid of the ΔABC. OA is the radius of the triangle.
OA = 2/3 AD
Let the side of a triangle a metres then BD = a/2 m.
Applying Pythagoras theorem in ΔABD,
AB2 = BD2 + AD2
⇒ AD2 = AB2 – BD2
⇒ AD2 = a2 – (a/2)2
⇒ AD2 = 3a2/4
⇒ AD = √3a/2
OA = 2/3 AD
⇒ 20 m = 2/3 × √3a/2
⇒ a = 20√3 m
So, the length of the string of the toy is 20√3 m.
|
40 videos|421 docs|51 tests
|

















