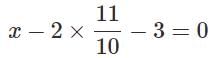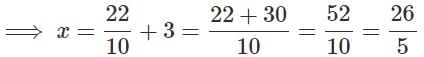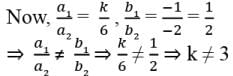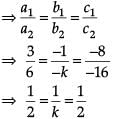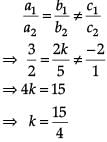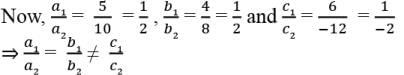Q1:
Question for Assertion & Reason Type Questions: Pair of Linear Equations in Two Variables
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): In a ΔABC, ∠C = 3∠B = 2(∠A + ∠B), then ∠A = 20°.
Reason (R): The angles of a triangle are x, y and 40°. The difference between the two angles x and y is 30°, then x = 85° and y = 55°.
Explanation
In case of assertion
Given that, ∠C = 3∠B = 2(∠A + ∠B)
3∠B = 2(∠A + ∠B)
3∠B = 2∠A + 2∠B
∠B = 2∠A
2 ∠A − ∠B = 0 ...(i)
We know that the sum of the measures of all angles of a triangle is 180°.
Therefore, ∠A + ∠B + ∠C = 180°
∠A + ∠B + 3∠B = 180°
∠A + 4∠B = 180° ...(ii)
Multiplying equation (i) by 4, we obtain
8∠A − 4∠B = 0 ...(iii)
Adding equations (ii) and (iii), we obtain
9∠A = 180°
∠A = 20°
∴ Assertion is correct.
In case of reason: Given that, x, y and 40° are the angels of a triangle.
x + y + 40° = 180°
[Since the sum of all the angels of a triangle is 180°.]
⇒ x + y = 140° ...(i)
Also, x – y = 30° ...(ii)
On adding Eqs. (i) and (ii), we get
2x = 170°
⇒ x = 170/2
∴ x = 85°
On putting x = 85° in Eq. (i), we get
85° + y = 140°
y = 140° – 85° = 55°
∴ y = 55°
Hence, the required values of x and y are 85° and 55°, respectively.
∴ Reason is correct.
Hence, both assertion and reason are correct but reason is not the correct explanation for assertion.
Report a problem
Q2:
Question for Assertion & Reason Type Questions: Pair of Linear Equations in Two Variables
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : The linear equations x - 2y - 3 = 0 and 3x + 4y - 20 = 0 = have exactly one solution.
Reason : The linear equations 2x + 3y - 0 = and 4x + 6y - 18 = 0 = have a unique solution.
Explanation
Let us first consider the assertion. It says that the linear equations x − 2y − 3 = 0 and 3x + 4y − 20 = 0 have exactly one solution.
Let x − 2y − 3 = 0--- (1) And, 3x + 4y − 20 = 0---(2)
In order to solve these equations, let us multiply the first equation by 3.
3(x − 2y − 3) = 3 × 0
⟹ 3x − 6y − 9 = 0 ----(3)
Subtracting equation 3 from equation 2, we get,
3x + 4y − 20 − (3x − 6y − 9) = 0
Removing the brackets, we get,
3x + 4y − 20 − 3x + 6y + 9 = 0
⟹ 10y − 11 = 0
⟹ y = 11 / 10
Now, in order to find the value of x, substituting the value of y in equation 1, we get,
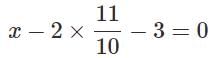
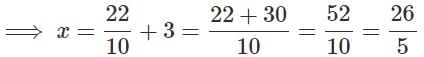
Thus, the pair of linear equations given possess exactly one solution (unique solution).
Hence, the assertion is correct.
Now, let us consider the reason. It says that the linear equations 2x + 3y − 9 = 0 and 4x + 6y − 8 = 0 have a unique solution.
Let 2x + 3y − 9 = 0---(1)
And, 4x + 6y − 18 = 0---(2)
In order to solve these equations, let us multiply the first equation by 2.
2(2x + 3y − 9) = 2 × 0
⟹4x + 6y − 18=0---(3)
As, equation 2 and 3 are same thus, thus the two linear equations given to us are coincident possessing infinitely many solutions.
Thus, the reason is not correct.
Thus, Assertion is correct but the Reason is incorrect.
Report a problem
Q3:
Question for Assertion & Reason Type Questions: Pair of Linear Equations in Two Variables
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : The value of k for which the system of linear equations kx – y = 2 and 6x – 2y = 3 has a unique solution is 3.
Reason : The system of linear equations a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 has a unique solution if a1/a2 ≠ b1/b2
Explanation
We know that the system of linear equations a
1x + b
1y + c
1 = 0 and a
2x + b
2y + c
2 = 0 has a unique solution if a
1/a
2 ≠ b
1/b
2So, Reason is correct For Assertion, we have, a1 = k, b1 = -1, c1 = -2, a2 = 6, b2 = -2 and c2 = -3
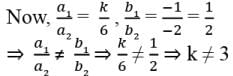
So, Assertion is not correct.
Report a problem
Q4:
Question for Assertion & Reason Type Questions: Pair of Linear Equations in Two Variables
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): The solution of the pair of linear equations x + y = 5 and 2x – 3y = 4 is x = 19/5 and y = 6/5.
Reason (R): The solution of the pair of linear equations 3x + 4y = 10 and 2x – 2y = 2 is x = 2 and y = 1.
Explanation
In case of assertion
By elimination method,
x + y = 5 ...(i)
2x – 3y = 4 ...(ii)
Multiplying equation (i) by (ii), we obtain
2x + 2y = 10 ...(iii)
Subtracting equation (ii) from equation (iii), we obtain
5y = 6
y = 6/5 …(iv)
Substituting the value in equation (i), we obtain
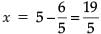
∴ x = 19/5 , y = 6/5
∴ Assertion is correct.
In case of reason:
By elimination method,
3x + 4y = 10 ...(i)
2x – 2y = 2 ...(ii)
Multiplying equation (ii) by 2, we obtain
4x – 4y = 4 ...(iii)
Adding equations (i) and (iii), we obtain
7x = 14
x = 2 ...(iv)
Substituting in equation (i), we obtain
6 + 4y = 10
4y = 4
y = 1
Hence, x = 2, y = 1
∴ Reason is correct.
Hence, both assertion and reason are correct but reason is not the correct explanation for assertion.
Report a problem
Q5:
Question for Assertion & Reason Type Questions: Pair of Linear Equations in Two Variables
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : 3x - 4y = 7 and 6x - 8y = k have infinite number of solution if k = 14 .
Reason : a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 have a unique solution if a1/a2 ≠ b1/b2.
Explanation
Let 3x − 4y = 7......(1)
6x − 8y = k......(2)
If k = 14 in equation (2) ⇒ 6x − 8y = 14
Now, (2) ÷ 2 ⇒ 3x − 4y = 7......(3)
Therefore, the lines represented by (1) and (3) shows that the lines are coincident and there are infinitely many solutions.
Hence, the Assertion is correct.
Clearly, the Reason is correct.
Since both the Assertion and Reason are correct but Reason is not the correct explanation for Assertion.
Report a problem
Q6:
Question for Assertion & Reason Type Questions: Pair of Linear Equations in Two Variables
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : The value of q = ±2, if x = 3, y = 1 is the solution of the line 2x + y – q2 – 3 = 0.
Reason : The solution of the line will satisfy the equation of the line.
Explanation
As x = 3, y = 1 is the solution of 2x + y – q
2 – 3 = 0
∴ 2 x 3 + 1 – q2 – 3 = 0
⇒ 4 – q2 = 0
⇒ q2 = 4 ⇒ q = ± 2
So, both A and R are correct and R explains A.
Report a problem
Q7:
Question for Assertion & Reason Type Questions: Pair of Linear Equations in Two Variables
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): If 4 chairs and 3 tables cost ₹ 2100 and 5 chairs and 2 tables cost ₹ 1750, then the cost of 1 chair is ₹ 150.Reason (R): Sum of the ages of a father and the son is 40 years. If father's age is 3 times that of his son, then the son's age is 12 years.
Explanation
In case of assertion
Let cost of 1 chair be ₹ x and cost of 1 table be ₹ y
According to the question,
4x +3y = 2100 ...(i)
and 5x +2y = 1750 ...(ii)
Multiplying eqn. (i) by 2 and eqn. (ii) by 3, we get
8x +6y = 4200 ...(iii)
15x + 6y = 5250 ...(iv)
eqn. (iv) – eqn. (iii)
⇒ 7x = 1050
∴ x = 150
Substituting the value of x in (i) we get y = 500
Thus, the cost of one chair and one table are ₹ 150 and ₹ 500 respectively.
∴ Assertion is correct.
In case of reason:
Let age of father and son be x and y respectively.
Then, x + y = 40 ...(i)
and x = 3y ...(ii)
By solving eqns. (i) and (ii), we get
x = 30 and y = 10
Thus, the ages of father and son are 30 years and 10 years.
∴ Reason is incorrect.
Hence, Assertion is correct but reason is incorrect.
Report a problem
Q8:
Question for Assertion & Reason Type Questions: Pair of Linear Equations in Two Variables
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : The lines 2x - 5y = 7 and 6x - 15y = 8 are parallel lines.
Reason : The system of linear equations a1x + b1y+ c1 = 0 and a2x + b2y + c2 = 0 have infinitely many solutions if a1/a2 = b1/b2 = c1/c2
Explanation
Two lines a
1x + b
1y + c
1 = 0 and a
2x + b
2y + c
2 = 0 are parallel if a
1/a
2 = b
1/b
2 ≠ c
1/c
2So, both A and R are correct but R does not explain A.
Report a problem
Q9:
Question for Assertion & Reason Type Questions: Pair of Linear Equations in Two Variables
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : A pair of linear equations has no solution (s) if it is represented by intersecting lines graphically.
Reason: If the pair of lines are intersecting, then the pair has unique solution and is called consistent pair of equations.
Explanation
We know that if the lines are parallel, then it has no solution.
So, Assertion is false. We know that if the lines are intersecting, then it has unique solution.
So, Reason is true.
Report a problem
Q10:
Question for Assertion & Reason Type Questions: Pair of Linear Equations in Two Variables
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): If the equation 3x – y + 8 = 0 and 6x – ky = –16 represent coincident lines, then the value of k = 2.
Reason (R): If the lines given by 3x + 2ky = 2 and 2x + 5y + 1 = 0 are parallel, then the value of k is 15.
Explanation
In case of assertion: 3x – y = –18 ...(i)
6x – ky = –16 ...(ii)
For coincident lines,
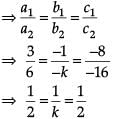
So, k = 2.
∴ Assertion is correct.
In case of reason:
For parallel lines (or no solution)
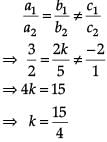
∴ Reason is incorrect.
Hence, assertion is correct but reason is incorrect.
Report a problem
Q11:
Question for Assertion & Reason Type Questions: Pair of Linear Equations in Two Variables
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : If kx - y - 2 = 0 and 6x - 2y - 3 = 0 = are inconsistent, then k = 3Reason : a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 are inconsistent of a1/a2 = b1/b2 ≠ c1/c2
Explanation
Let kx − y − 2 = 0......(1)
6x − 2y − 3 = 0......(2)
For the equation to be inconsistent
⇒ a1/a2 = b1/b2 ≠ c1/c2
⇒ k/6 = -1/-2 ≠ -2/-3
∴ k = 3
Therefore the Assertion is correct.
Clearly, the Reason is correct.
Since both the Assertion and Reason are correct and Reason is a correct explanation of Assertion.
Report a problem
Q12:
Question for Assertion & Reason Type Questions: Pair of Linear Equations in Two Variables
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : The number of common solutions for the system of linear equations 5x + 4y + 6 = 0 and 10x + 8y = 12 is zeroReason : The system of linear equations a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 has a unique solution if a1/a2 ≠ b1/b2
Explanation
We know that the system of linear equations a
1x + b
1y + c
1 = 0 and a
2x + b
2y + c
2 = 0 has a unique solution if a
1/a
2 ≠ b
1/b
2So, Reason is correct
For Assertion, we have, a1 = 5, b1 = 4, c1 = 6, a2 = 10, b2 = 8 and c2 = -12
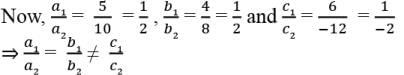
So, the pair of linear equations has no solution and hence Assertion is correct.
But reason (R) is not the correct explanation of assertion (A).
Report a problem
Q13:
Question for Assertion & Reason Type Questions: Pair of Linear Equations in Two Variables
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): For all real values of c, the pair of equations x – 2y = 8 and 5x – 10y = c have a unique solution.
Reason (R): Two lines are given to be parallel. The equation of one of the lines is 4x + 3y = 14, 12x + 9y = 5.
Explanation
In case of assertion
x – 2y = 8 ...(i)
5x – 10 = c ...(ii)
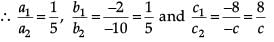
As a1/a2 = b1/b2 , so system of linear equations can never have unique solution.
∴ Assertion is incorrect.
In case of reason:
The equation of one line is 4x + 3y = 14.
We know that if two lines a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 are parallel, then
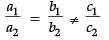
or
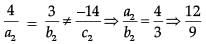
Hence, one of the possible, second parallel line is 12x + 9y = 5.
∴ Reason is correct Hence, assertion is incorrect but reason is correct.
Report a problem
Q14:
Question for Assertion & Reason Type Questions: Pair of Linear Equations in Two Variables
Try yourself:Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : Pair of linear equations : 9x + 3y + 12 = 0, 18x + 6y + 24 = 0 have infinitely many solutions.
Reason : Pair of linear equations a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 have infinitely many solutions, a1/a2 = b1/b2 = c1/c2
Explanation
From the given equations, we have
9/18 = 3/6 = 12/24
1/2 = 1/2 = 1/2 i.e, a1/a2 = b1/b2 = c1/c2
So, both A and R are correct and R explains A.
Report a problem
Q15:
Question for Assertion & Reason Type Questions: Pair of Linear Equations in Two Variables
Try yourself:Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : The value of k for which the system of linear equations 3x – 4y = 7 and 6x - 8y = k have infinite number of solution is 14.
Reason : The system of linear equations a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 has a unique solution if a1/a2 ≠ b1/b2
Explanation
We know that the system of linear equations a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 has infinitely many solutions if a1/a2 = b1/b2 = c1/c2.
So, Reason is not correct For Assertion, we have, a1 = 3, b1 = -4, c1 = -7, a2 = 6, b2 = -8 and c2 = -k
Report a problem