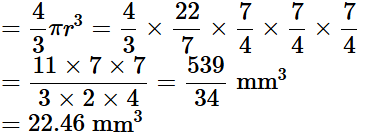Surface Areas and Volume Class 9 Worksheet Maths
Multiple Choice Questions
Q1: Surface area of bowl of radius r cm is
(a) 4πr2
(b) 2πr2
(c) 3πr2
(d) πr2
Ans: (c)
 View Answer
View AnswerSol: The area of a circle of radius r is πr2
Thus if the hemisphere is meant to include the base then the surface area is 2πr2 + πr2 = 3πr2
Q2: A conical tent is 10 m high and the radius of its base is 24 m then slant height of the tent is
(a) 26
(b) 27
(c) 28
(d) 29
Ans: (a)
 View Answer
View AnswerSol: Height (h) of conical tent = 10 m
Radius (r) of conical tent = 24 m
Let the slant height of the tent be l
l2 = h2 + r2
l2 = (10)2 + (24)2
l2 = 100 + 576
l2 = 676
l = √676
l = √262
l = 26 m
Therefore, the slant height of the tent is 26 m.
Q3: Diameter of the base of a cone is 10.5 cm and its slant height is 10 cm . then curved surface area.
(a) 155 cm2
(b) 165 cm2
(c) 150 cm2
(d) none of these
Ans: 165 cm2
 View Answer
View AnswerSol: Diameter of the base of the cone is 10.5 cm and slant height is 10 cm.
Curved surface area of a right circular cone of base radius, ['r']and slant height, l is πr.
Diameter, d = 10.5 cm
Radius, r = 10.5 / 2 cm= 5.25 cm
Slant height, l = 10 cm
Curved surface area = πrl
= 3.14 × 5.25 × 10 = 165 cm
Thus, curved surface area of the cone = 165 cm2.
Q4: The surface area of a sphere of radius 5.6 cm is
(a) 96.8π cm2
(b) 94.08π cm2
(c) 90.08π cm2
(d) none of these
Ans: (b)
 View Answer
View AnswerSol: Given radius of sphere = 5.6 cm
Surface area of sphere = 4πr2
= 4 × 3.14 × (5.6)2
Surface area of sphere = 393.88 cm2
Q5: The height and the slant height of a cone are 21 cm and 28 cm respectively then volume of cone
(a) 7556 cm3
(b) 7646 cm3
(c) 7546 cm3
(d) None of these
Ans: (c)
 View Answer
View AnswerSol: Volume of the cone = 1/3 πr2h
Given
Slant height = l= 28 cm
Height of cone = h= 21 cm
Let radius of cone = r cm
l2 = h2 + r2
282 = 212 + r2
282 - 212 = r2
r2 = 282 - 212
r2 = (28 - 21)(28 + 21)
r2 =(7)(49)
r = √7(49)
r = √7(7)2
r = 7√7 cm
Volume of the cone = 1/3 πr2 h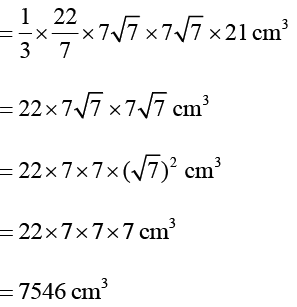
Fill in the blank
Q1: Surface area of sphere of diameter 14cm is____________.
Ans: 616cm2
 View Answer
View AnswerSol: Given Diameter of sphere =14cm radius =7cm
surface area of sphere = 4πr2 = 4π(7)2
= 4 × 3.14 × 49
surface area of sphere = 616cm2
Q2: Volume of hollow cylinder is ______________.
Ans: π(R2−r2)h
 View Answer
View AnswerSol: The formula to calculate the volume of a hollow cylinder is given as,
Volume of hollow cylinder =π(R2−r2)h cubic units,
where, 'R′ is the outer radius, ' r ' is the inner radius, and, ' h ' is the height of the hollow cylinder.
Q3: Find the volume of a sphere whose surface area 154cm2 is_________________.
Ans: 179.67cm3
 View Answer
View AnswerSol: Given surface area of sphere =154cm2
Let radius of the sphere = r cm
4πr2 = 1544 × 227 × r2
=154r2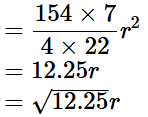 Volume of sphere =4/3πr3
Volume of sphere =4/3πr3 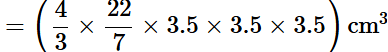 =179.67cm3
=179.67cm3
Q4: A hemispherical bowl has a radius of 3.5cm. What would be the volume of water it would contain__________.
Ans: 89.8cm3
 View Answer
View AnswerSol: The volume of water the bowl contain =2/3πr3
Radius of hemisphere =r=3.5cm
The volume of water the bowl can contain =2/3πr3
= 2/3 × 22/7 × 3.5 × 3.5 × 3.5cm3
= 89.8cm3
Q5: The formula for the volume of a cone is __________.
Ans: 13 π r2 h
 View Answer
View AnswerSol: The formula for the volume of a cone is: 13 π r2 h
True / False
Q1: The volume of a sphere is equal to two-third of the volume of a cylinder whose height and diameter are equal to the diameter of the sphere.
Ans: True
 View Answer
View AnswerSol: Let the radius of the sphere = r.
According to the question,
height and diameter of cylinder = diameter of sphere.
So, the radius of the cylinder = r
And, the height of the cylinder = 2r
We know that,
Volume of sphere = 2/3 volume of cylinder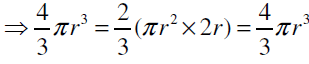 Hence, the given statement “the volume of a sphere is equal to two-third of the volume of a cylinder whose height and diameter are equal to the diameter of the sphere” is true.
Hence, the given statement “the volume of a sphere is equal to two-third of the volume of a cylinder whose height and diameter are equal to the diameter of the sphere” is true.
Q2: If the radius of a right circular cone is halved and height is doubled, the volume will remain unchanged.
Ans: False
 View Answer
View AnswerSol: Let the original radius of the cone = r
Let height of the cone = h.
The volume of cone = 1/3 πr2h
Now, when radius of a height circular cone is halved and height is doubled, then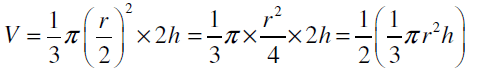 We can observe that the new volume = half of the original volume.
We can observe that the new volume = half of the original volume.
Hence, the given statement “if the radius of a right circular cone is halved and height is doubled, the volume will remain unchanged” is false.
Q3: If the radius of a cylinder is doubled and its curved surface area is not changed, the height must be halved.
Ans: True
 View Answer
View AnswerSol: Let radius of the cylinder = r
Height of the cylinder = h
Then, curved surface area of the cylinder, CSA = 2πrh
According to the question,
Radius is doubled and curved surface area is not changed.
New radius of the cylinder, R = 2r
New curved surface area of the cylinder, CSA’ = 2πrh …(i)
Alternate case:
When R = 2r and CSA’ = 2πrh
But curved surface area of cylinder in this case, CSA’= 2πRh = 2π(2r)h = 4πrh …(ii)
Comparing equations (i) and (ii),
We get,
Since, 2πrh ≠ 4πrh
equation (i) ≠ equation (ii)
Thus, if h = h/2 (height is halved)
Then,
CSA’ = 2π(2r)(h/2) = 2πrh
Hence, the given statement “If the radius of a cylinder is doubled and its curved surface area is not changed, the height must be halved” is true.
Q4: Doubling the radius of a sphere will double its volume.
Ans: False
 View Answer
View AnswerSol: Formula for the volume of a sphere:
V = 43 π r3
If the radius is doubled (i.e., r becomes 2r), then the new volume V' is:
V' = 43 π (2r)3 = 43 π 8r3 = 8 × 43 π r3
Thus, doubling the radius increases the volume by a factor of 8, not 2.
Q5: The total surface area of a cone is the sum of its lateral surface area and the area of its circular base.
Ans: True
 View Answer
View AnswerSol: The total surface area of a cone is the sum of its lateral surface area and the area of its circular base:
Lateral Surface Area = π r l
Area of Circular Base = π r2
Total Surface Area = π r l + π r2
For a cone with radius r and slant height l, the total surface area A is given by:
A = π r l + π r2
Subjective Type Questions
Q1: Diameter of the base of a cone is 10.5 cm and its slant height is 10 cm . Find its curved surface area and its total surface area.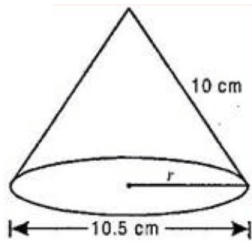
Ans: Diameter = 10.5 cm
Slant height of cone (l ) = 10 cm
Curved surface area of cone,=165 cm2
Total surface area of cone,
Q2: A Joker's cap is in the form of a right circular cone of base radius 7 cm and height 24 cm. Find the area of the sheet required to make 10 such caps.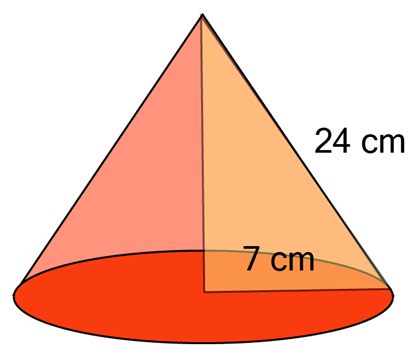
Ans: Radius of cap (r) = 7cm, Height of cap (h) =24 cm
Slant height of the cone (l)Area of sheet required to make a cap = CSA of cone = πrl
∴ Area of sheet required to make 10 caps = 10 × 550 = 5500 cm2
Q3: Find the surface area of a sphere of diameter:
(i) 14cm
Ans: (i) Diameter of sphere = 14cm,
Therefore, Radius of sphere = 14/2 = 7cm
Surface area of sphere = 4πr2 = 4 × 22/7 × 7 × 7 = 616cm2
(ii) 21cm
Ans: Diameter of sphere = 21cm
∴ Radius of sphere =21/2cm
Surface area of sphere = 4πr2 = 4 × 22/7 × 21/2 × 21/2
=1386cm2
(iii) 3.5cm
Ans: Diameter of sphere = 3.5cm
∴ Radius of sphere =3.5/2 = 1.75cm
Surface area of sphere = 4πr2 = 4 × 22/7 × 1.75 × 1.75
= 38.5cm2
Q4: A hemispherical bowl is made of steel, 0.25cm thick. The inner radius of the bowl is 5cm . Find the outer curved surface area of the bowl.
Ans: Inner radius of bowl (r)= 5cm
Thickness of steel (t) = 0.25cm
∴ Outer radius of bowl (R) = r + t = 5 + 0.25 = 5.25cm
∴ Outer curved surface area of bowl = 2πR2 = 2 × 22/7 × 5.25 × 5.25
= 2 × 22/7 × 21/4 × 21/4
= 693/4 =173.25cm2
Q5: Twenty-seven solid iron spheres, each of radius r and surface area S are melted to form a sphere with surface area S '. Find the:
(i) radius r ' of the new sphere.
Ans: Volume of 1 sphere, V = 4/3πr3
Volume of 27 solid sphere
= 27 × 4/3πr3
Let r1 is the radius of the new sphere.
Volume of new sphere = Volume of 27 solid sphere
(ii) ratio of S and S '.
Ans:
S1 : S = 9 : 1
S : S1 = 1 : 9
Q6: A capsule of medicine is in the shape of a sphere of diameter 3.5mm . How much medicine (in mm3) is needed to fill this capsule?
Ans: Diameter of spherical capsule = 3.5mm
∴ Radius of spherical capsule (r) = 3.5/2 = 35/20 = 7/4mm
Medicine needed to fill the capsule = Volume of sphere
|
40 videos|420 docs|51 tests
|
FAQs on Surface Areas and Volume Class 9 Worksheet Maths
| 1. What is the formula for calculating the surface area of a cylinder? |  |
| 2. How do you find the volume of a cone? |  |
| 3. What is the difference between surface area and volume? |  |
| 4. How can I calculate the surface area of a sphere? |  |
| 5. What are the units used for measuring surface area and volume? |  |

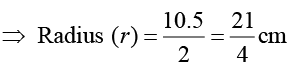 Slant height of cone (l ) = 10 cm
Slant height of cone (l ) = 10 cm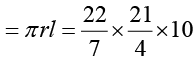 =165 cm2
=165 cm2 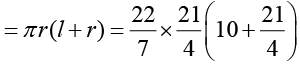
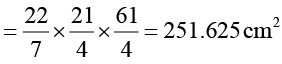
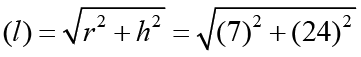
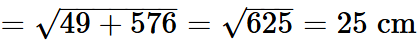
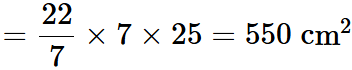 ∴ Area of sheet required to make 10 caps = 10 × 550 = 5500 cm2
∴ Area of sheet required to make 10 caps = 10 × 550 = 5500 cm2 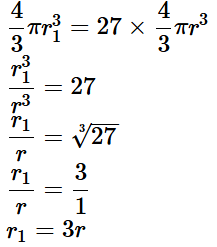
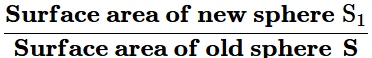
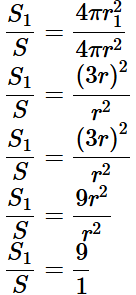 S1 : S = 9 : 1
S1 : S = 9 : 1