Class 8 Maths Chapter 8 Practice Question Answers - Algebraic Expressions and Identities

Clear all your Class 8 doubts with EduRev Join for Free

Join for Free

Q1: Identify the type of expressions:
(i) x²y + xy²
(ii) 564xy
(iii) -8x + 4y
(iv) x² + x + 7
(v) xy + yz + zp + px + 9xy
Sol:
(i) x²y + xy² = Binomial
(ii) 564xy = Monomial
(iii) -8x + 4y = Binomial
(iv) x² + x + 7 = Trinomial
(v) xy + yz + zp + px + 9xy = Polynomial

Q2: Find the area of a square with side 5x²y
Sol:
Given that the side of square = 5x²y
Area of square = side² = (5x²y)² = 25x⁴y²

Q3: Simplify the following expressions:
(i) (x + y + z)(x + y – z)
(ii) x2(x – 3y2) – xy(y2 – 2xy) – x(y3 – 5x2)
(iii) 2x2(x + 2) – 3x (x2 – 3) – 5x(x + 5)
Sol:
Notes: “+” × “+” = “+”, “-” × “-” = “+”, and “+” × “-” = “-”.
(i) (x + y + z)(x + y – z)
= x2 + xy – xz + yx + y2 – yz + zx + zy – z²
Add similar terms like xy and yx, xz and zx, and yz and zy. Then simplify and rearrange.
= x² + y² – z² + 2xy
(ii) x²(x – 3y²) – xy(y² – 2xy) – x(y³ – 5x²)
= x³ – 3x²y² – xy³ + 2x²y² – xy³ + 5x³
Now, add the similar terms and rearrange.
= x³ + 5x³ – 3x²y² + 2x²y² – xy³ – xy³
= 6x³ – x²y² – 2xy³
(iii) 2x²(x + 2) – 3x (x² – 3) – 5x(x + 5)
= 2x³ + 4x² – 3x³ + 9x – 5x² – 25x
= 2x³ – 3x³ – 5x² + 4x² + 9x – 25x
= -x³ – x² – 16x

Q4: Subtract the following polynomials.
(i) (7x + 2) from (-6x + 8)
(ii) 3xy + 5yz – 7xz + 1 from -4xy + 2yz – 2xz + 5xyz + 1
(iii) 2x²y²– 3xy + 4 from 4x²y² + 10xy
Sol:
(i) (7x + 2) from (-6x + 8)
= (-6x + 8) – (7x + 2)
= -6x + 8 – (7x + 2)
= -6x + 8 – 7x – 2
= -13x + 6
(ii) 3xy + 5yz – 7xz + 1 from -4xy + 2yz – 2xz + 5xyz + 1

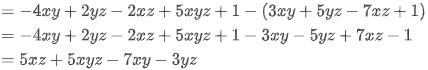
(iii) 2x²y²– 3xy + 4 from 4x²y² + 10xy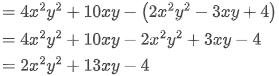


Q5: Simplify 7x²(3x – 9) + 3 and find its values for x = 4 and x = 6
Sol:

7x²(3x – 9) + 3
Solve for 7x²(3x – 9)
= (7x² × 3x)  – (7x² × 9) (using distributive law: a(b – c) = ab – ac)
= 21x³ – 63x²
So, 7x²(3x – 9) + 3
= 21x³ – 63x2 + 3
Now, for x = 4,
21x³ – 63x² + 3

= 21 × 4³ – 63 × 4² + 3

= 1344 – 1008 + 3

= 336 + 3 = 339

Now, for x = 6,

21x³ – 63x²

= 21 × 6³ – 63 × 6² + 3

= 2268 + 3

= 2271

Q6: Calculate the volume of a cuboidal box whose dimensions are 5x × 3x² × 7x⁴
Sol:
Given,
Length = 5x
Breadth = 3x²
Height = 7x⁴
Volume of cuboid = Length × Breadth × Height
= 5x × 3x² × 7x⁴
Multiply 5, 3, and 7
= 105xx²x⁴
Use exponents rule: x^a × x^b = x^(a+b)
So, 105xx²x⁴ = 105x¹⁺²⁺⁴ 
= 105x⁷

Q7: Add the following polynomials.
(i) x + y + xy, x – z + yx, and z + x + xz
(ii) 2x²y²– 3xy + 4, 5 + 7xy – 3x²y², and 4x²y² + 10xy
(iii) -3a²b², (–5/2) a²b², 4a²b², and (⅔) a²b²
Sol:
(i) x + y + xy, x – z + yx, and z + x + xz
= (x + y + xy) + (x – z + yx) + (z + x + xz)
= x + y + xy + x – z + yx + z + x + xz
Add similar elements and rearrange.
= 2xy + xz + 3x + y
(ii) 2x²y²– 3xy + 4, 5 + 7xy – 3x²y², and 4x²y² + 10xy
= (2x²y²– 3xy + 4) + (5 + 7xy – 3x²y²) + (4x²y² + 10xy)
= 2x²y² – 3xy + 4 + 5 + 7xy – 3x²y² + 4x²y² + 10xy
Add similar elements and rearrange.
= 3x²y² + 14xy + 9
(iii) -3a²b², (–5/2) a²b², 4a²b², and (⅔) a²b²


Q8: Calculate the area of a rectangle whose length and breadths are given as 3x²y m and 5xy² m respectively.
Sol:
Given,
Length = 3x²y m
Breadth = 5xy² m
Area of rectangle = Length × Breadth
= (3x²y × 5xy²) = (3 × 5) × x²y × xy² = 15x³y³ m²

Q9: Identify terms and their coefficients from the following expressions:
(i) 6x²y² – 9x²y²z²+ 4z²
(ii) 3xyz – 8y
(iii) 6.1x – 5.9xy + 2.3y
Sol:
(i) 6x²y² – 9x²y²z²+ 4z²
Terms = 6x²y², -9x²y²z², and 4z²
Coefficients = 6, -9, and 4
(ii) 3xyz – 8y
Terms = 3xyz, and -8y
Coefficients = 3, and -8
(iii) 6.1x – 5.9xy + 2.3y
Terms = 6.1x, – 5.9xy, and 2.3y
Coefficients = 6.1, – 5.9 and 2.3

Q10: Using suitable algebraic identity, solve 10922
Sol:
Use the algebraic identity: (a + b)² = a² + 2ab + b²
Now, 109² = 1000 + 92
So, 1092² = (1000 + 92)²
(1000 + 92)² = ( 1000 )² + 2 × 1000 × 92 + ( 92 )²
= 1000000 + 184000 + 8464
Thus, 1092² = 1192464.